Paul Vitanyi
CWI and University of Amsterdam
Approximation of the Two-Part MDL Code
Sep 15, 2008Abstract:Approximation of the optimal two-part MDL code for given data, through successive monotonically length-decreasing two-part MDL codes, has the following properties: (i) computation of each step may take arbitrarily long; (ii) we may not know when we reach the optimum, or whether we will reach the optimum at all; (iii) the sequence of models generated may not monotonically improve the goodness of fit; but (iv) the model associated with the optimum has (almost) the best goodness of fit. To express the practically interesting goodness of fit of individual models for individual data sets we have to rely on Kolmogorov complexity.
Similarity of Objects and the Meaning of Words
Feb 17, 2006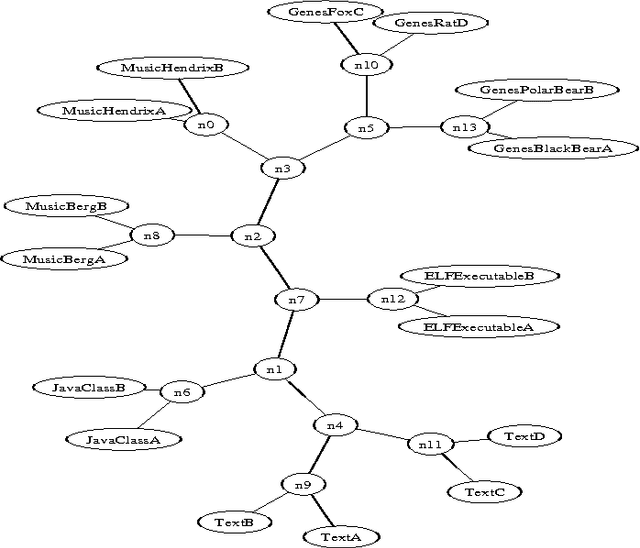
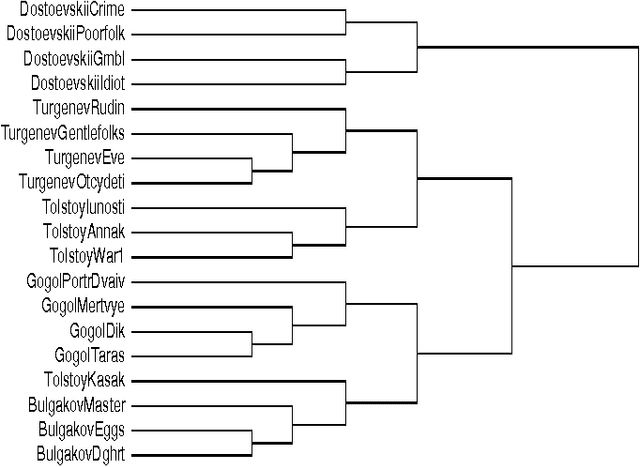
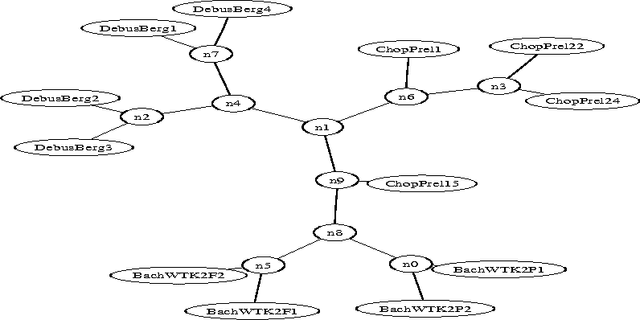
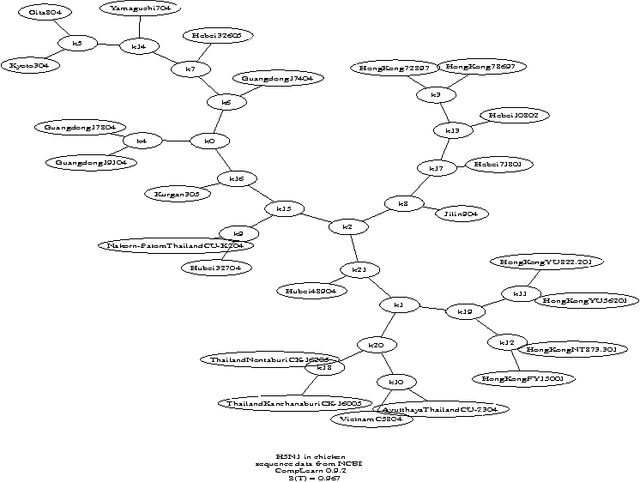
Abstract:We survey the emerging area of compression-based, parameter-free, similarity distance measures useful in data-mining, pattern recognition, learning and automatic semantics extraction. Given a family of distances on a set of objects, a distance is universal up to a certain precision for that family if it minorizes every distance in the family between every two objects in the set, up to the stated precision (we do not require the universal distance to be an element of the family). We consider similarity distances for two types of objects: literal objects that as such contain all of their meaning, like genomes or books, and names for objects. The latter may have literal embodyments like the first type, but may also be abstract like ``red'' or ``christianity.'' For the first type we consider a family of computable distance measures corresponding to parameters expressing similarity according to particular featuresdistances generated by web users corresponding to particular semantic relations between the (names for) the designated objects. For both families we give universal similarity distance measures, incorporating all particular distance measures in the family. In the first case the universal distance is based on compression and in the second case it is based on Google page counts related to search terms. In both cases experiments on a massive scale give evidence of the viability of the approaches. between pairs of literal objects. For the second type we consider similarity
Universal Similarity
Jul 07, 2005Abstract:We survey a new area of parameter-free similarity distance measures useful in data-mining, pattern recognition, learning and automatic semantics extraction. Given a family of distances on a set of objects, a distance is universal up to a certain precision for that family if it minorizes every distance in the family between every two objects in the set, up to the stated precision (we do not require the universal distance to be an element of the family). We consider similarity distances for two types of objects: literal objects that as such contain all of their meaning, like genomes or books, and names for objects. The latter may have literal embodyments like the first type, but may also be abstract like ``red'' or ``christianity.'' For the first type we consider a family of computable distance measures corresponding to parameters expressing similarity according to particular features between pairs of literal objects. For the second type we consider similarity distances generated by web users corresponding to particular semantic relations between the (names for) the designated objects. For both families we give universal similarity distance measures, incorporating all particular distance measures in the family. In the first case the universal distance is based on compression and in the second case it is based on Google page counts related to search terms. In both cases experiments on a massive scale give evidence of the viability of the approaches.
The similarity metric
Aug 05, 2004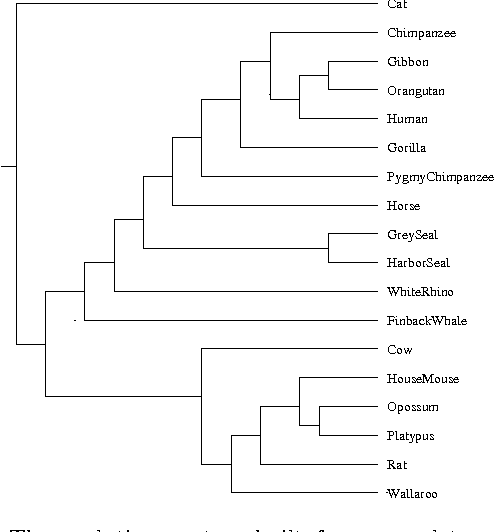
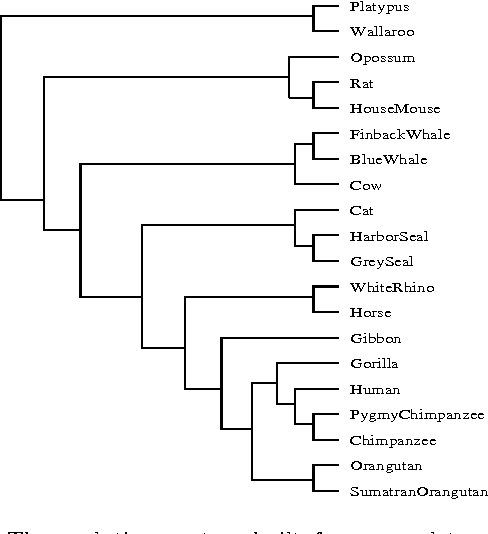
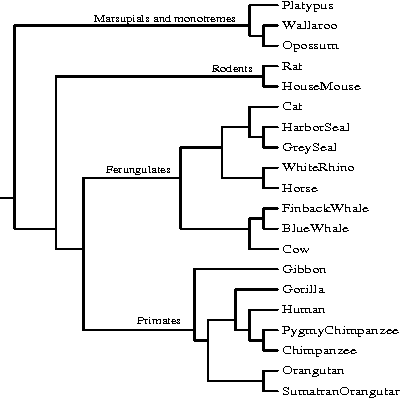
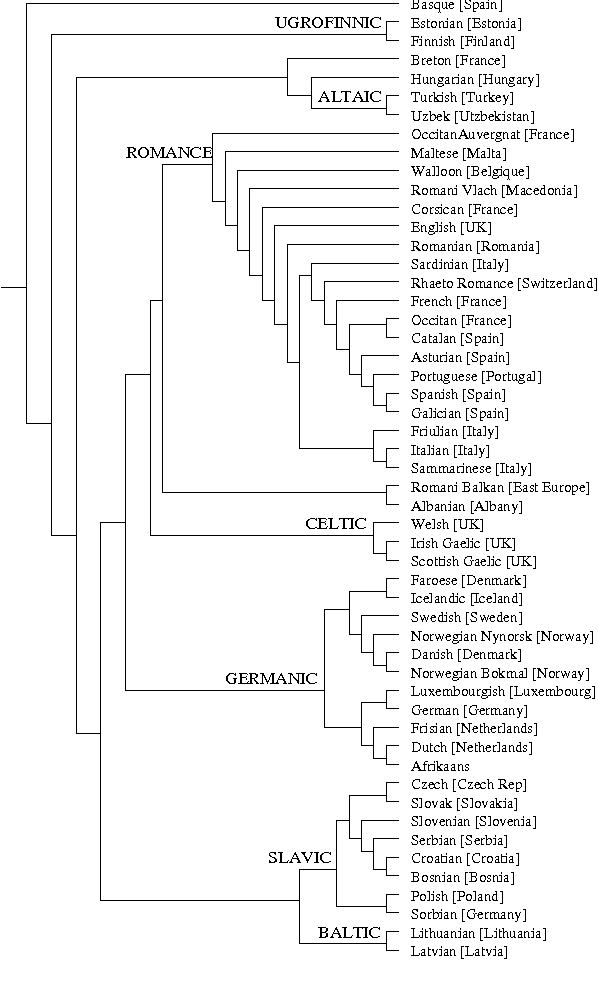
Abstract:A new class of distances appropriate for measuring similarity relations between sequences, say one type of similarity per distance, is studied. We propose a new ``normalized information distance'', based on the noncomputable notion of Kolmogorov complexity, and show that it is in this class and it minorizes every computable distance in the class (that is, it is universal in that it discovers all computable similarities). We demonstrate that it is a metric and call it the {\em similarity metric}. This theory forms the foundation for a new practical tool. To evidence generality and robustness we give two distinctive applications in widely divergent areas using standard compression programs like gzip and GenCompress. First, we compare whole mitochondrial genomes and infer their evolutionary history. This results in a first completely automatic computed whole mitochondrial phylogeny tree. Secondly, we fully automatically compute the language tree of 52 different languages.
Clustering by compression
Apr 09, 2004

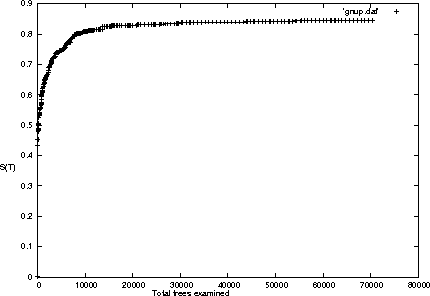

Abstract:We present a new method for clustering based on compression. The method doesn't use subject-specific features or background knowledge, and works as follows: First, we determine a universal similarity distance, the normalized compression distance or NCD, computed from the lengths of compressed data files (singly and in pairwise concatenation). Second, we apply a hierarchical clustering method. The NCD is universal in that it is not restricted to a specific application area, and works across application area boundaries. A theoretical precursor, the normalized information distance, co-developed by one of the authors, is provably optimal but uses the non-computable notion of Kolmogorov complexity. We propose precise notions of similarity metric, normal compressor, and show that the NCD based on a normal compressor is a similarity metric that approximates universality. To extract a hierarchy of clusters from the distance matrix, we determine a dendrogram (binary tree) by a new quartet method and a fast heuristic to implement it. The method is implemented and available as public software, and is robust under choice of different compressors. To substantiate our claims of universality and robustness, we report evidence of successful application in areas as diverse as genomics, virology, languages, literature, music, handwritten digits, astronomy, and combinations of objects from completely different domains, using statistical, dictionary, and block sorting compressors. In genomics we presented new evidence for major questions in Mammalian evolution, based on whole-mitochondrial genomic analysis: the Eutherian orders and the Marsupionta hypothesis against the Theria hypothesis.
Algorithmic Clustering of Music
Mar 24, 2003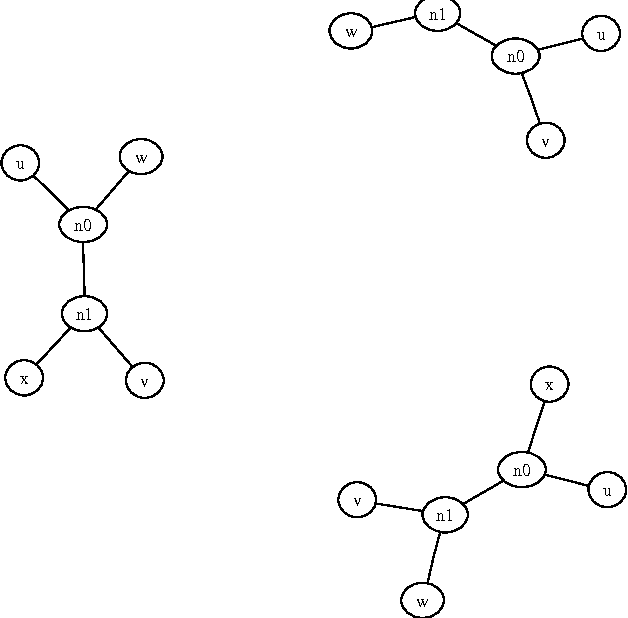
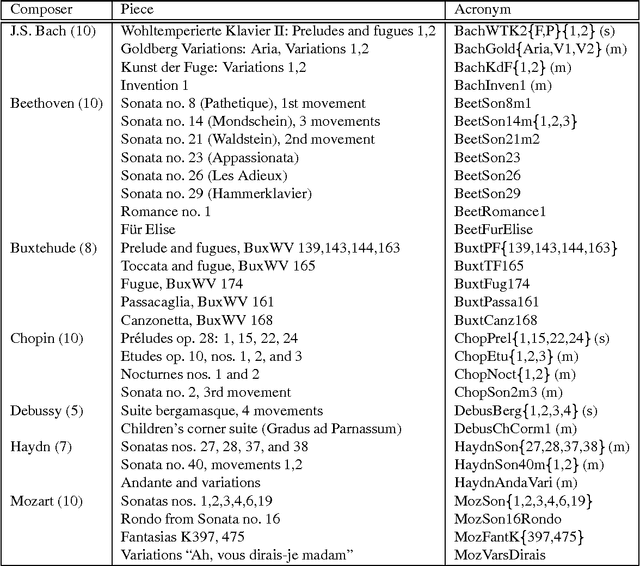

Abstract:We present a fully automatic method for music classification, based only on compression of strings that represent the music pieces. The method uses no background knowledge about music whatsoever: it is completely general and can, without change, be used in different areas like linguistic classification and genomics. It is based on an ideal theory of the information content in individual objects (Kolmogorov complexity), information distance, and a universal similarity metric. Experiments show that the method distinguishes reasonably well between various musical genres and can even cluster pieces by composer.
Sharpening Occam's Razor
Oct 10, 2002Abstract:We provide a new representation-independent formulation of Occam's razor theorem, based on Kolmogorov complexity. This new formulation allows us to: (i) Obtain better sample complexity than both length-based and VC-based versions of Occam's razor theorem, in many applications. (ii) Achieve a sharper reverse of Occam's razor theorem than previous work. Specifically, we weaken the assumptions made in an earlier publication, and extend the reverse to superpolynomial running times.
Algorithmic Statistics
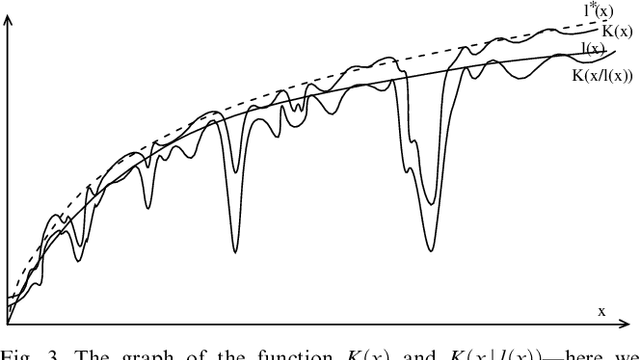
Oct 09, 2001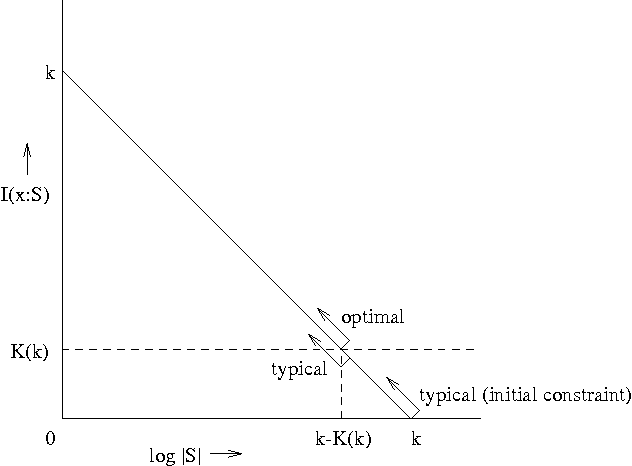
Abstract:While Kolmogorov complexity is the accepted absolute measure of information content of an individual finite object, a similarly absolute notion is needed for the relation between an individual data sample and an individual model summarizing the information in the data, for example, a finite set (or probability distribution) where the data sample typically came from. The statistical theory based on such relations between individual objects can be called algorithmic statistics, in contrast to classical statistical theory that deals with relations between probabilistic ensembles. We develop the algorithmic theory of statistic, sufficient statistic, and minimal sufficient statistic. This theory is based on two-part codes consisting of the code for the statistic (the model summarizing the regularity, the meaningful information, in the data) and the model-to-data code. In contrast to the situation in probabilistic statistical theory, the algorithmic relation of (minimal) sufficiency is an absolute relation between the individual model and the individual data sample. We distinguish implicit and explicit descriptions of the models. We give characterizations of algorithmic (Kolmogorov) minimal sufficient statistic for all data samples for both description modes--in the explicit mode under some constraints. We also strengthen and elaborate earlier results on the ``Kolmogorov structure function'' and ``absolutely non-stochastic objects''--those rare objects for which the simplest models that summarize their relevant information (minimal sufficient statistics) are at least as complex as the objects themselves. We demonstrate a close relation between the probabilistic notions and the algorithmic ones.
* LaTeX, 22 pages, 1 figure, with correction to the published journal version
The Generalized Universal Law of Generalization
Jan 29, 2001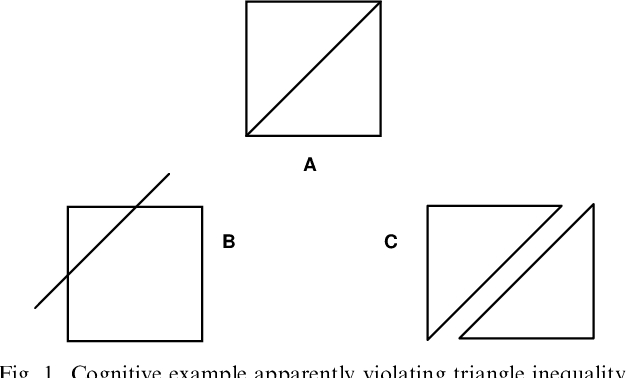
Abstract:It has been argued by Shepard that there is a robust psychological law that relates the distance between a pair of items in psychological space and the probability that they will be confused with each other. Specifically, the probability of confusion is a negative exponential function of the distance between the pair of items. In experimental contexts, distance is typically defined in terms of a multidimensional Euclidean space-but this assumption seems unlikely to hold for complex stimuli. We show that, nonetheless, the Universal Law of Generalization can be derived in the more complex setting of arbitrary stimuli, using a much more universal measure of distance. This universal distance is defined as the length of the shortest program that transforms the representations of the two items of interest into one another: the algorithmic information distance. It is universal in the sense that it minorizes every computable distance: it is the smallest computable distance. We show that the universal law of generalization holds with probability going to one-provided the confusion probabilities are computable. We also give a mathematically more appealing form
Applying MDL to Learning Best Model Granularity
May 23, 2000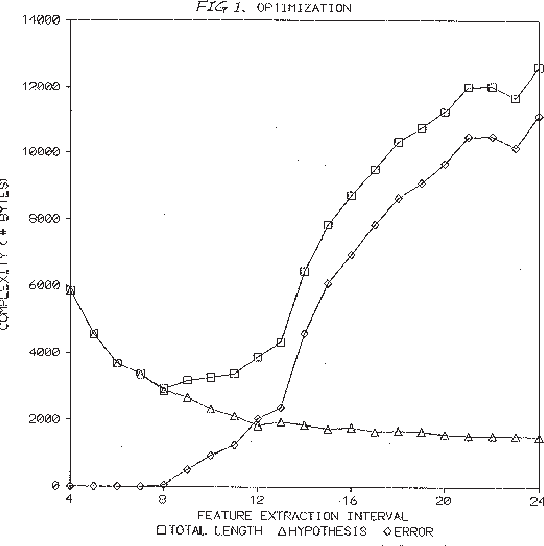
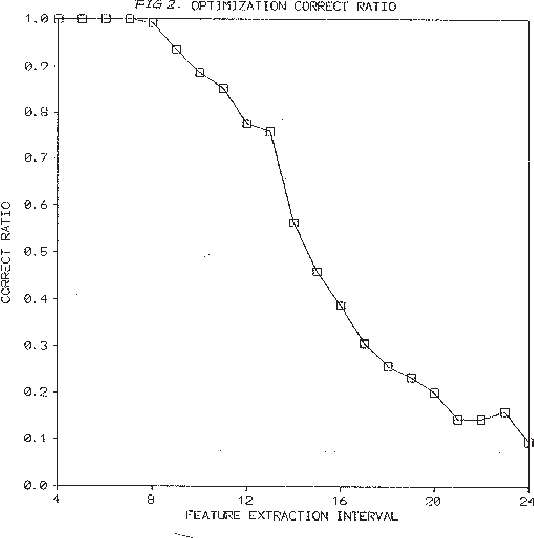
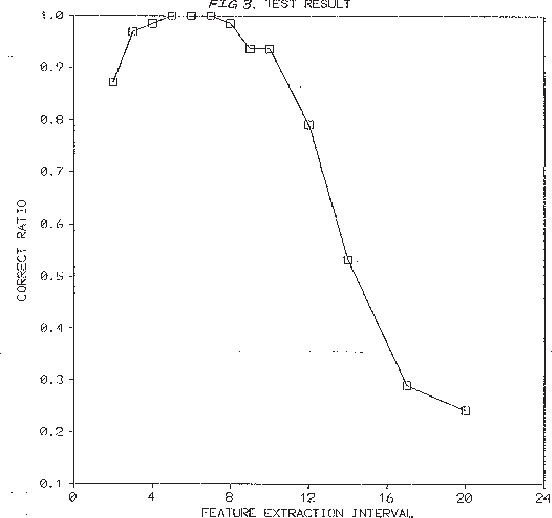
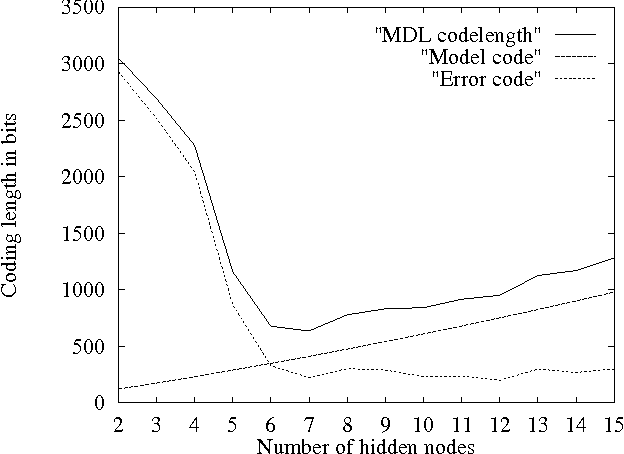
Abstract:The Minimum Description Length (MDL) principle is solidly based on a provably ideal method of inference using Kolmogorov complexity. We test how the theory behaves in practice on a general problem in model selection: that of learning the best model granularity. The performance of a model depends critically on the granularity, for example the choice of precision of the parameters. Too high precision generally involves modeling of accidental noise and too low precision may lead to confusion of models that should be distinguished. This precision is often determined ad hoc. In MDL the best model is the one that most compresses a two-part code of the data set: this embodies ``Occam's Razor.'' In two quite different experimental settings the theoretical value determined using MDL coincides with the best value found experimentally. In the first experiment the task is to recognize isolated handwritten characters in one subject's handwriting, irrespective of size and orientation. Based on a new modification of elastic matching, using multiple prototypes per character, the optimal prediction rate is predicted for the learned parameter (length of sampling interval) considered most likely by MDL, which is shown to coincide with the best value found experimentally. In the second experiment the task is to model a robot arm with two degrees of freedom using a three layer feed-forward neural network where we need to determine the number of nodes in the hidden layer giving best modeling performance. The optimal model (the one that extrapolizes best on unseen examples) is predicted for the number of nodes in the hidden layer considered most likely by MDL, which again is found to coincide with the best value found experimentally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge