Rudi Cilibrasi
CWI
The Google Similarity Distance
May 30, 2007



Abstract:Words and phrases acquire meaning from the way they are used in society, from their relative semantics to other words and phrases. For computers the equivalent of `society' is `database,' and the equivalent of `use' is `way to search the database.' We present a new theory of similarity between words and phrases based on information distance and Kolmogorov complexity. To fix thoughts we use the world-wide-web as database, and Google as search engine. The method is also applicable to other search engines and databases. This theory is then applied to construct a method to automatically extract similarity, the Google similarity distance, of words and phrases from the world-wide-web using Google page counts. The world-wide-web is the largest database on earth, and the context information entered by millions of independent users averages out to provide automatic semantics of useful quality. We give applications in hierarchical clustering, classification, and language translation. We give examples to distinguish between colors and numbers, cluster names of paintings by 17th century Dutch masters and names of books by English novelists, the ability to understand emergencies, and primes, and we demonstrate the ability to do a simple automatic English-Spanish translation. Finally, we use the WordNet database as an objective baseline against which to judge the performance of our method. We conduct a massive randomized trial in binary classification using support vector machines to learn categories based on our Google distance, resulting in an a mean agreement of 87% with the expert crafted WordNet categories.
* 15 pages, 10 figures; changed some text/figures/notation/part of theorem. Incorporated referees comments. This is the final published version up to some minor changes in the galley proofs
A New Quartet Tree Heuristic for Hierarchical Clustering
Jun 11, 2006



Abstract:We consider the problem of constructing an an optimal-weight tree from the 3*(n choose 4) weighted quartet topologies on n objects, where optimality means that the summed weight of the embedded quartet topologiesis optimal (so it can be the case that the optimal tree embeds all quartets as non-optimal topologies). We present a heuristic for reconstructing the optimal-weight tree, and a canonical manner to derive the quartet-topology weights from a given distance matrix. The method repeatedly transforms a bifurcating tree, with all objects involved as leaves, achieving a monotonic approximation to the exact single globally optimal tree. This contrasts to other heuristic search methods from biological phylogeny, like DNAML or quartet puzzling, which, repeatedly, incrementally construct a solution from a random order of objects, and subsequently add agreement values.
Similarity of Objects and the Meaning of Words
Feb 17, 2006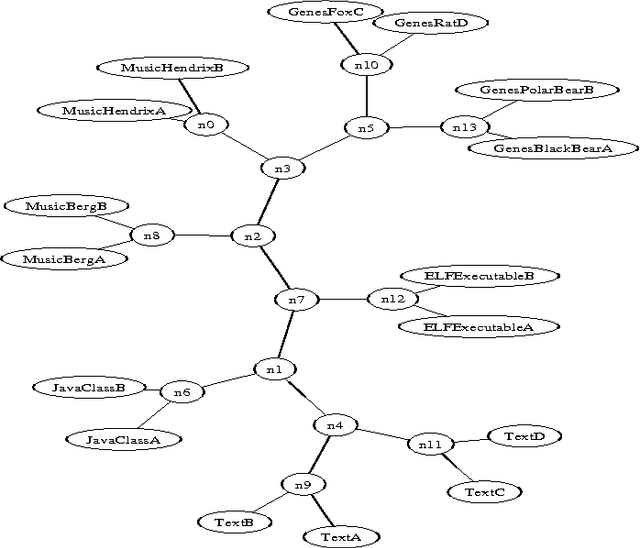
Abstract:We survey the emerging area of compression-based, parameter-free, similarity distance measures useful in data-mining, pattern recognition, learning and automatic semantics extraction. Given a family of distances on a set of objects, a distance is universal up to a certain precision for that family if it minorizes every distance in the family between every two objects in the set, up to the stated precision (we do not require the universal distance to be an element of the family). We consider similarity distances for two types of objects: literal objects that as such contain all of their meaning, like genomes or books, and names for objects. The latter may have literal embodyments like the first type, but may also be abstract like ``red'' or ``christianity.'' For the first type we consider a family of computable distance measures corresponding to parameters expressing similarity according to particular featuresdistances generated by web users corresponding to particular semantic relations between the (names for) the designated objects. For both families we give universal similarity distance measures, incorporating all particular distance measures in the family. In the first case the universal distance is based on compression and in the second case it is based on Google page counts related to search terms. In both cases experiments on a massive scale give evidence of the viability of the approaches. between pairs of literal objects. For the second type we consider similarity
Clustering by compression
Apr 09, 2004

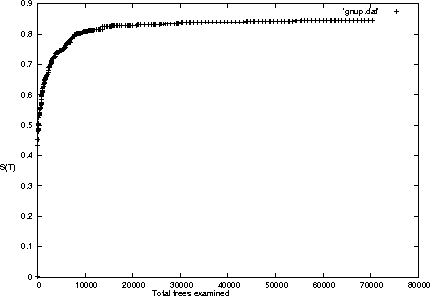

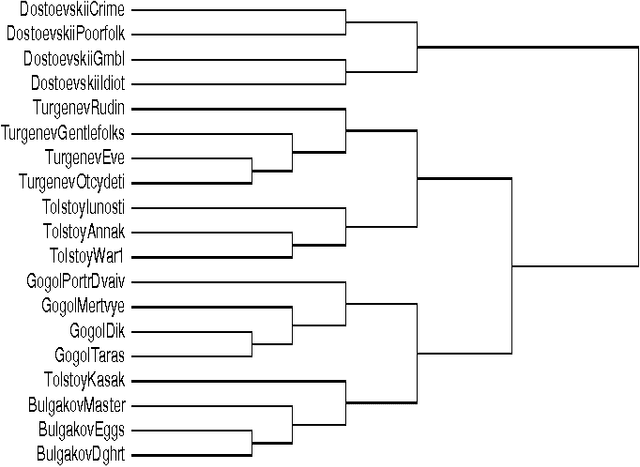
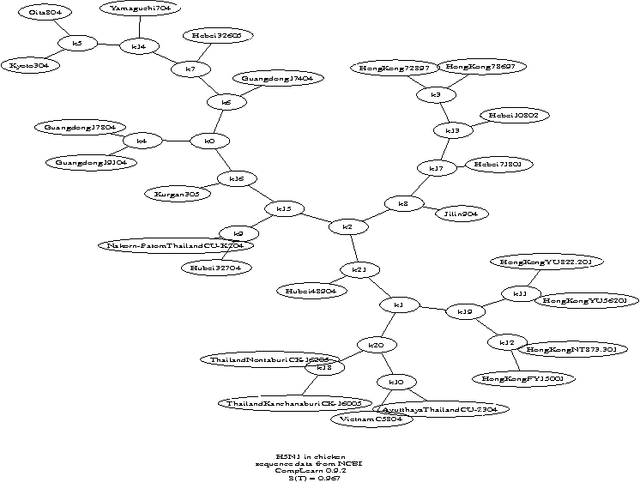
Abstract:We present a new method for clustering based on compression. The method doesn't use subject-specific features or background knowledge, and works as follows: First, we determine a universal similarity distance, the normalized compression distance or NCD, computed from the lengths of compressed data files (singly and in pairwise concatenation). Second, we apply a hierarchical clustering method. The NCD is universal in that it is not restricted to a specific application area, and works across application area boundaries. A theoretical precursor, the normalized information distance, co-developed by one of the authors, is provably optimal but uses the non-computable notion of Kolmogorov complexity. We propose precise notions of similarity metric, normal compressor, and show that the NCD based on a normal compressor is a similarity metric that approximates universality. To extract a hierarchy of clusters from the distance matrix, we determine a dendrogram (binary tree) by a new quartet method and a fast heuristic to implement it. The method is implemented and available as public software, and is robust under choice of different compressors. To substantiate our claims of universality and robustness, we report evidence of successful application in areas as diverse as genomics, virology, languages, literature, music, handwritten digits, astronomy, and combinations of objects from completely different domains, using statistical, dictionary, and block sorting compressors. In genomics we presented new evidence for major questions in Mammalian evolution, based on whole-mitochondrial genomic analysis: the Eutherian orders and the Marsupionta hypothesis against the Theria hypothesis.
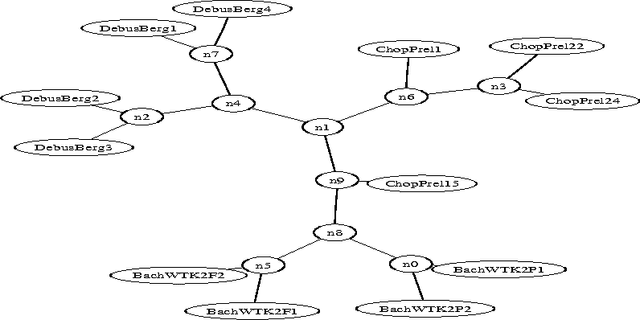
Algorithmic Clustering of Music
Mar 24, 2003
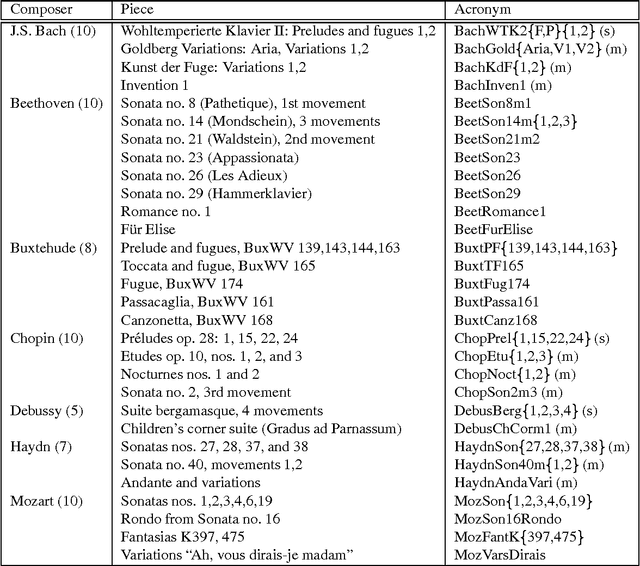

Abstract:We present a fully automatic method for music classification, based only on compression of strings that represent the music pieces. The method uses no background knowledge about music whatsoever: it is completely general and can, without change, be used in different areas like linguistic classification and genomics. It is based on an ideal theory of the information content in individual objects (Kolmogorov complexity), information distance, and a universal similarity metric. Experiments show that the method distinguishes reasonably well between various musical genres and can even cluster pieces by composer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge