John Tromp
CWI
Sharpening Occam's Razor
Oct 10, 2002Abstract:We provide a new representation-independent formulation of Occam's razor theorem, based on Kolmogorov complexity. This new formulation allows us to: (i) Obtain better sample complexity than both length-based and VC-based versions of Occam's razor theorem, in many applications. (ii) Achieve a sharper reverse of Occam's razor theorem than previous work. Specifically, we weaken the assumptions made in an earlier publication, and extend the reverse to superpolynomial running times.
Algorithmic Statistics
Oct 09, 2001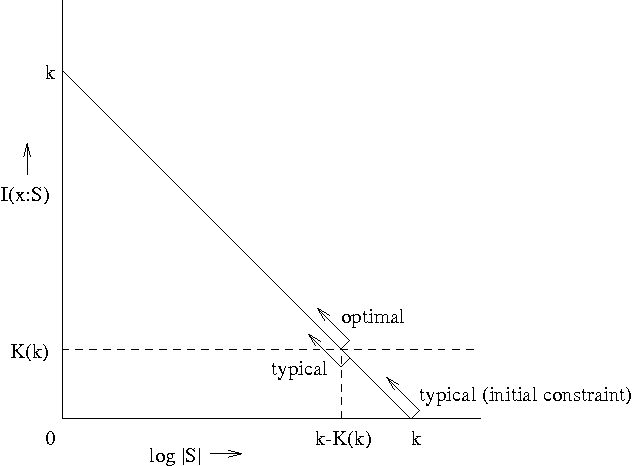
Abstract:While Kolmogorov complexity is the accepted absolute measure of information content of an individual finite object, a similarly absolute notion is needed for the relation between an individual data sample and an individual model summarizing the information in the data, for example, a finite set (or probability distribution) where the data sample typically came from. The statistical theory based on such relations between individual objects can be called algorithmic statistics, in contrast to classical statistical theory that deals with relations between probabilistic ensembles. We develop the algorithmic theory of statistic, sufficient statistic, and minimal sufficient statistic. This theory is based on two-part codes consisting of the code for the statistic (the model summarizing the regularity, the meaningful information, in the data) and the model-to-data code. In contrast to the situation in probabilistic statistical theory, the algorithmic relation of (minimal) sufficiency is an absolute relation between the individual model and the individual data sample. We distinguish implicit and explicit descriptions of the models. We give characterizations of algorithmic (Kolmogorov) minimal sufficient statistic for all data samples for both description modes--in the explicit mode under some constraints. We also strengthen and elaborate earlier results on the ``Kolmogorov structure function'' and ``absolutely non-stochastic objects''--those rare objects for which the simplest models that summarize their relevant information (minimal sufficient statistics) are at least as complex as the objects themselves. We demonstrate a close relation between the probabilistic notions and the algorithmic ones.
* LaTeX, 22 pages, 1 figure, with correction to the published journal version
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge