Imagining and building wise machines: The centrality of AI metacognition

Recent advances in artificial intelligence (AI) have produced systems capable of increasingly sophisticated performance on cognitive tasks. However, AI systems still struggle in critical ways: unpredictable and novel environments (robustness), lack of transparency in their reasoning (explainability), challenges in communication and commitment (cooperation), and risks due to potential harmful actions (safety). We argue that these shortcomings stem from one overarching failure: AI systems lack wisdom. Drawing from cognitive and social sciences, we define wisdom as the ability to navigate intractable problems - those that are ambiguous, radically uncertain, novel, chaotic, or computationally explosive - through effective task-level and metacognitive strategies. While AI research has focused on task-level strategies, metacognition - the ability to reflect on and regulate one's thought processes - is underdeveloped in AI systems. In humans, metacognitive strategies such as recognizing the limits of one's knowledge, considering diverse perspectives, and adapting to context are essential for wise decision-making. We propose that integrating metacognitive capabilities into AI systems is crucial for enhancing their robustness, explainability, cooperation, and safety. By focusing on developing wise AI, we suggest an alternative to aligning AI with specific human values - a task fraught with conceptual and practical difficulties. Instead, wise AI systems can thoughtfully navigate complex situations, account for diverse human values, and avoid harmful actions. We discuss potential approaches to building wise AI, including benchmarking metacognitive abilities and training AI systems to employ wise reasoning. Prioritizing metacognition in AI research will lead to systems that act not only intelligently but also wisely in complex, real-world situations.

Mental Sampling in Multimodal Representations

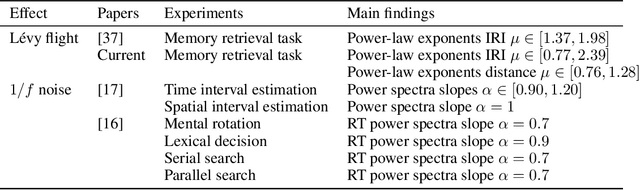
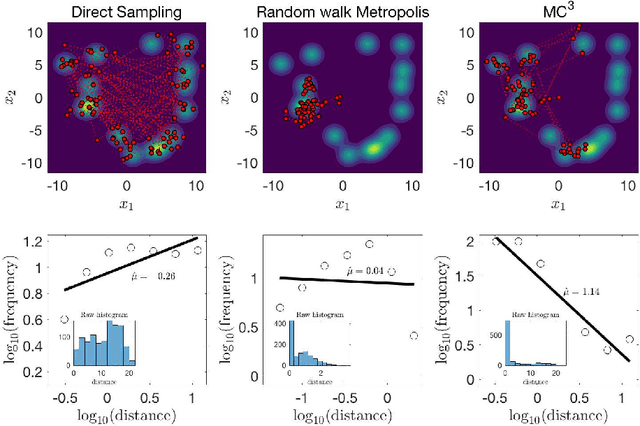
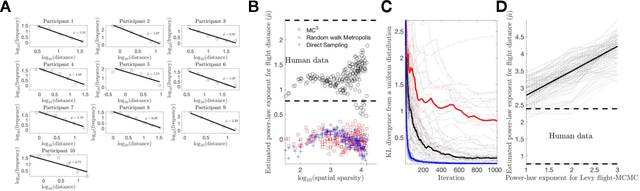
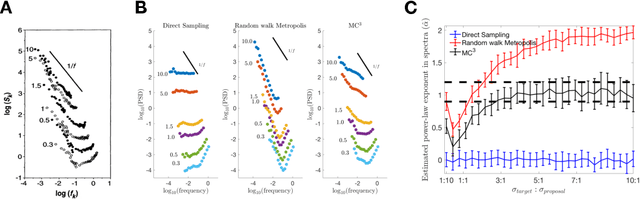
Both resources in the natural environment and concepts in a semantic space are distributed "patchily", with large gaps in between the patches. To describe people's internal and external foraging behavior, various random walk models have been proposed. In particular, internal foraging has been modeled as sampling: in order to gather relevant information for making a decision, people draw samples from a mental representation using random-walk algorithms such as Markov chain Monte Carlo (MCMC). However, two common empirical observations argue against simple sampling algorithms such as MCMC. First, the spatial structure is often best described by a L\'evy flight distribution: the probability of the distance between two successive locations follows a power-law on the distances. Second, the temporal structure of the sampling that humans and other animals produce have long-range, slowly decaying serial correlations characterized as $1/f$-like fluctuations. We propose that mental sampling is not done by simple MCMC, but is instead adapted to multimodal representations and is implemented by Metropolis-coupled Markov chain Monte Carlo (MC$^3$), one of the first algorithms developed for sampling from multimodal distributions. MC$^3$ involves running multiple Markov chains in parallel but with target distributions of different temperatures, and it swaps the states of the chains whenever a better location is found. Heated chains more readily traverse valleys in the probability landscape to propose moves to far-away peaks, while the colder chains make the local steps that explore the current peak or patch. We show that MC$^3$ generates distances between successive samples that follow a L\'evy flight distribution and $1/f$-like serial correlations, providing a single mechanistic account of these two puzzling empirical phenomena.

Identification of Probabilities

Within psychology, neuroscience and artificial intelligence, there has been increasing interest in the proposal that the brain builds probabilistic models of sensory and linguistic input: that is, to infer a probabilistic model from a sample. The practical problems of such inference are substantial: the brain has limited data and restricted computational resources. But there is a more fundamental question: is the problem of inferring a probabilistic model from a sample possible even in principle? We explore this question and find some surprisingly positive and general results. First, for a broad class of probability distributions characterised by computability restrictions, we specify a learning algorithm that will almost surely identify a probability distribution in the limit given a finite i.i.d. sample of sufficient but unknown length. This is similarly shown to hold for sequences generated by a broad class of Markov chains, subject to computability assumptions. The technical tool is the strong law of large numbers. Second, for a large class of dependent sequences, we specify an algorithm which identifies in the limit a computable measure for which the sequence is typical, in the sense of Martin-Lof (there may be more than one such measure). The technical tool is the theory of Kolmogorov complexity. We analyse the associated predictions in both cases. We also briefly consider special cases, including language learning, and wider theoretical implications for psychology.

Identification of Probabilities of Languages

We consider the problem of inferring the probability distribution associated with a language, given data consisting of an infinite sequence of elements of the languge. We do this under two assumptions on the algorithms concerned: (i) like a real-life algorothm it has round-off errors, and (ii) it has no round-off errors. Assuming (i) we (a) consider a probability mass function of the elements of the language if the data are drawn independent identically distributed (i.i.d.), provided the probability mass function is computable and has a finite expectation. We give an effective procedure to almost surely identify in the limit the target probability mass function using the Strong Law of Large Numbers. Second (b) we treat the case of possibly incomputable probabilistic mass functions in the above setting. In this case we can only pointswize converge to the target probability mass function almost surely. Third (c) we consider the case where the data are dependent assuming they are typical for at least one computable measure and the language is finite. There is an effective procedure to identify by infinite recurrence a nonempty subset of the computable measures according to which the data is typical. Here we use the theory of Kolmogorov complexity. Assuming (ii) we obtain the weaker result for (a) that the target distribution is identified by infinite recurrence almost surely; (b) stays the same as under assumption (i). We consider the associated predictions.

Algorithmic Identification of Probabilities

TThe problem is to identify a probability associated with a set of natural numbers, given an infinite data sequence of elements from the set. If the given sequence is drawn i.i.d. and the probability mass function involved (the target) belongs to a computably enumerable (c.e.) or co-computably enumerable (co-c.e.) set of computable probability mass functions, then there is an algorithm to almost surely identify the target in the limit. The technical tool is the strong law of large numbers. If the set is finite and the elements of the sequence are dependent while the sequence is typical in the sense of Martin-L\"of for at least one measure belonging to a c.e. or co-c.e. set of computable measures, then there is an algorithm to identify in the limit a computable measure for which the sequence is typical (there may be more than one such measure). The technical tool is the theory of Kolmogorov complexity. We give the algorithms and consider the associated predictions.

Language learning from positive evidence, reconsidered: A simplicity-based approach

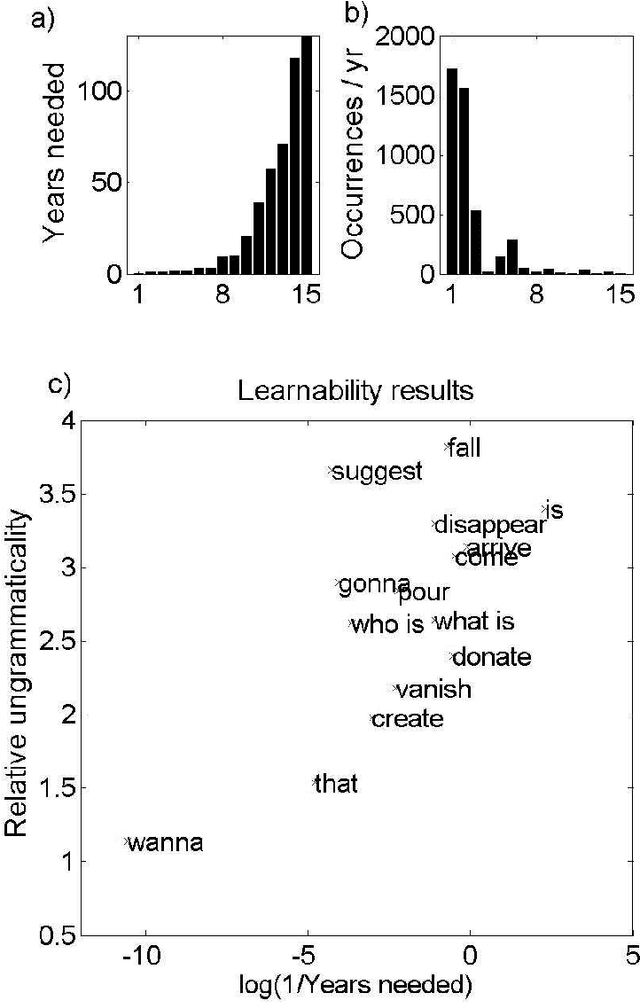
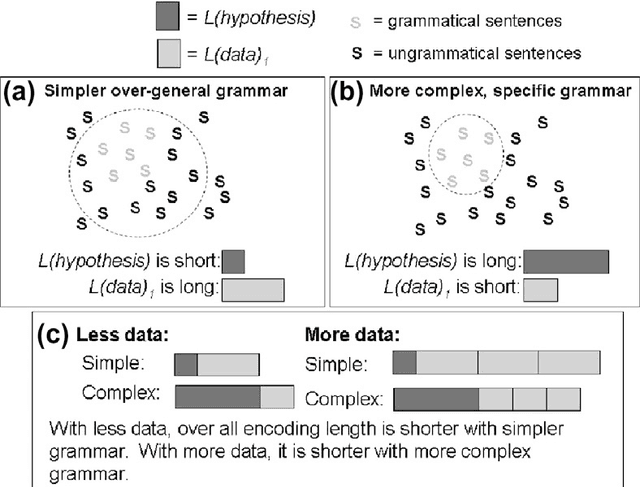
Children learn their native language by exposure to their linguistic and communicative environment, but apparently without requiring that their mistakes are corrected. Such learning from positive evidence has been viewed as raising logical problems for language acquisition. In particular, without correction, how is the child to recover from conjecturing an over-general grammar, which will be consistent with any sentence that the child hears? There have been many proposals concerning how this logical problem can be dissolved. Here, we review recent formal results showing that the learner has sufficient data to learn successfully from positive evidence, if it favours the simplest encoding of the linguistic input. Results include the ability to learn a linguistic prediction, grammaticality judgements, language production, and form-meaning mappings. The simplicity approach can also be scaled-down to analyse the ability to learn a specific linguistic constructions, and is amenable to empirical test as a framework for describing human language acquisition.

The probabilistic analysis of language acquisition: Theoretical, computational, and experimental analysis

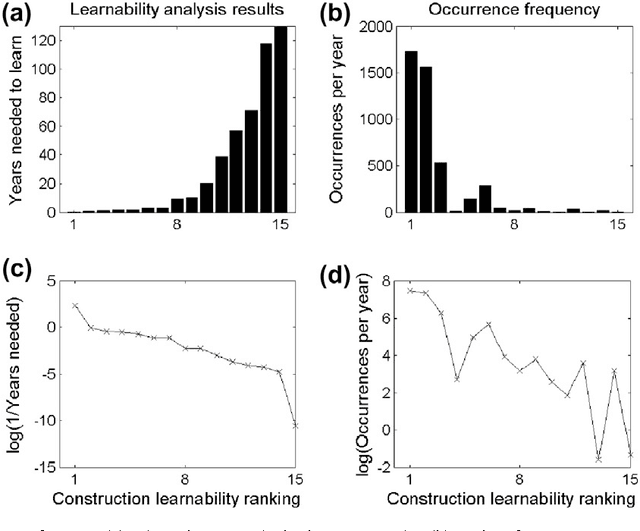
There is much debate over the degree to which language learning is governed by innate language-specific biases, or acquired through cognition-general principles. Here we examine the probabilistic language acquisition hypothesis on three levels: We outline a novel theoretical result showing that it is possible to learn the exact generative model underlying a wide class of languages, purely from observing samples of the language. We then describe a recently proposed practical framework, which quantifies natural language learnability, allowing specific learnability predictions to be made for the first time. In previous work, this framework was used to make learnability predictions for a wide variety of linguistic constructions, for which learnability has been much debated. Here, we present a new experiment which tests these learnability predictions. We find that our experimental results support the possibility that these linguistic constructions are acquired probabilistically from cognition-general principles.

The Generalized Universal Law of Generalization

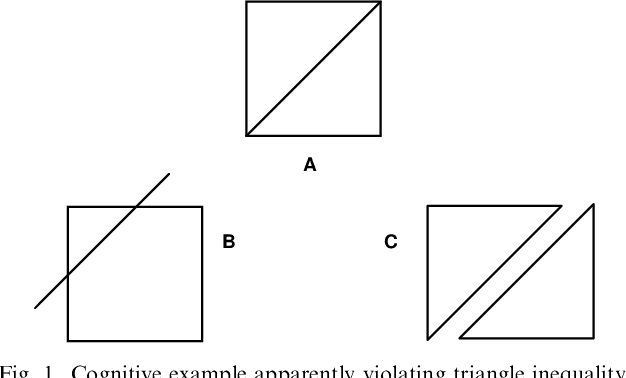
It has been argued by Shepard that there is a robust psychological law that relates the distance between a pair of items in psychological space and the probability that they will be confused with each other. Specifically, the probability of confusion is a negative exponential function of the distance between the pair of items. In experimental contexts, distance is typically defined in terms of a multidimensional Euclidean space-but this assumption seems unlikely to hold for complex stimuli. We show that, nonetheless, the Universal Law of Generalization can be derived in the more complex setting of arbitrary stimuli, using a much more universal measure of distance. This universal distance is defined as the length of the shortest program that transforms the representations of the two items of interest into one another: the algorithmic information distance. It is universal in the sense that it minorizes every computable distance: it is the smallest computable distance. We show that the universal law of generalization holds with probability going to one-provided the confusion probabilities are computable. We also give a mathematically more appealing form