Learning Only On Boundaries: a Physics-Informed Neural operator for Solving Parametric Partial Differential Equations in Complex Geometries

Recently deep learning surrogates and neural operators have shown promise in solving partial differential equations (PDEs). However, they often require a large amount of training data and are limited to bounded domains. In this work, we present a novel physics-informed neural operator method to solve parametrized boundary value problems without labeled data. By reformulating the PDEs into boundary integral equations (BIEs), we can train the operator network solely on the boundary of the domain. This approach reduces the number of required sample points from $O(N^d)$ to $O(N^{d-1})$, where $d$ is the domain's dimension, leading to a significant acceleration of the training process. Additionally, our method can handle unbounded problems, which are unattainable for existing physics-informed neural networks (PINNs) and neural operators. Our numerical experiments show the effectiveness of parametrized complex geometries and unbounded problems.

An Expert's Guide to Training Physics-informed Neural Networks

Physics-informed neural networks (PINNs) have been popularized as a deep learning framework that can seamlessly synthesize observational data and partial differential equation (PDE) constraints. Their practical effectiveness however can be hampered by training pathologies, but also oftentimes by poor choices made by users who lack deep learning expertise. In this paper we present a series of best practices that can significantly improve the training efficiency and overall accuracy of PINNs. We also put forth a series of challenging benchmark problems that highlight some of the most prominent difficulties in training PINNs, and present comprehensive and fully reproducible ablation studies that demonstrate how different architecture choices and training strategies affect the test accuracy of the resulting models. We show that the methods and guiding principles put forth in this study lead to state-of-the-art results and provide strong baselines that future studies should use for comparison purposes. To this end, we also release a highly optimized library in JAX that can be used to reproduce all results reported in this paper, enable future research studies, as well as facilitate easy adaptation to new use-case scenarios.

PDE-Refiner: Achieving Accurate Long Rollouts with Neural PDE Solvers

Time-dependent partial differential equations (PDEs) are ubiquitous in science and engineering. Recently, mostly due to the high computational cost of traditional solution techniques, deep neural network based surrogates have gained increased interest. The practical utility of such neural PDE solvers relies on their ability to provide accurate, stable predictions over long time horizons, which is a notoriously hard problem. In this work, we present a large-scale analysis of common temporal rollout strategies, identifying the neglect of non-dominant spatial frequency information, often associated with high frequencies in PDE solutions, as the primary pitfall limiting stable, accurate rollout performance. Based on these insights, we draw inspiration from recent advances in diffusion models to introduce PDE-Refiner; a novel model class that enables more accurate modeling of all frequency components via a multistep refinement process. We validate PDE-Refiner on challenging benchmarks of complex fluid dynamics, demonstrating stable and accurate rollouts that consistently outperform state-of-the-art models, including neural, numerical, and hybrid neural-numerical architectures. We further demonstrate that PDE-Refiner greatly enhances data efficiency, since the denoising objective implicitly induces a novel form of spectral data augmentation. Finally, PDE-Refiner's connection to diffusion models enables an accurate and efficient assessment of the model's predictive uncertainty, allowing us to estimate when the surrogate becomes inaccurate.

PPDONet: Deep Operator Networks for Fast Prediction of Steady-State Solutions in Disk-Planet Systems

We develop a tool, which we name Protoplanetary Disk Operator Network (PPDONet), that can predict the solution of disk-planet interactions in protoplanetary disks in real-time. We base our tool on Deep Operator Networks (DeepONets), a class of neural networks capable of learning non-linear operators to represent deterministic and stochastic differential equations. With PPDONet we map three scalar parameters in a disk-planet system -- the Shakura \& Sunyaev viscosity $\alpha$, the disk aspect ratio $h_\mathrm{0}$, and the planet-star mass ratio $q$ -- to steady-state solutions of the disk surface density, radial velocity, and azimuthal velocity. We demonstrate the accuracy of the PPDONet solutions using a comprehensive set of tests. Our tool is able to predict the outcome of disk-planet interaction for one system in less than a second on a laptop. A public implementation of PPDONet is available at \url{https://github.com/smao-astro/PPDONet}.

Gaussian Process Port-Hamiltonian Systems: Bayesian Learning with Physics Prior

Data-driven approaches achieve remarkable results for the modeling of complex dynamics based on collected data. However, these models often neglect basic physical principles which determine the behavior of any real-world system. This omission is unfavorable in two ways: The models are not as data-efficient as they could be by incorporating physical prior knowledge, and the model itself might not be physically correct. We propose Gaussian Process Port-Hamiltonian systems (GP-PHS) as a physics-informed Bayesian learning approach with uncertainty quantification. The Bayesian nature of GP-PHS uses collected data to form a distribution over all possible Hamiltonians instead of a single point estimate. Due to the underlying physics model, a GP-PHS generates passive systems with respect to designated inputs and outputs. Further, the proposed approach preserves the compositional nature of Port-Hamiltonian systems.

Ensemble learning for Physics Informed Neural Networks: a Gradient Boosting approach

While the popularity of physics-informed neural networks (PINNs) is steadily rising, to this date, PINNs have not been successful in simulating multi-scale and singular perturbation problems. In this work, we present a new training paradigm referred to as "gradient boosting" (GB), which significantly enhances the performance of physics informed neural networks (PINNs). Rather than learning the solution of a given PDE using a single neural network directly, our algorithm employs a sequence of neural networks to achieve a superior outcome. This approach allows us to solve problems presenting great challenges for traditional PINNs. Our numerical experiments demonstrate the effectiveness of our algorithm through various benchmarks, including comparisons with finite element methods and PINNs. Furthermore, this work also unlocks the door to employing ensemble learning techniques in PINNs, providing opportunities for further improvement in solving PDEs.

Variational Autoencoding Neural Operators

Unsupervised learning with functional data is an emerging paradigm of machine learning research with applications to computer vision, climate modeling and physical systems. A natural way of modeling functional data is by learning operators between infinite dimensional spaces, leading to discretization invariant representations that scale independently of the sample grid resolution. Here we present Variational Autoencoding Neural Operators (VANO), a general strategy for making a large class of operator learning architectures act as variational autoencoders. For this purpose, we provide a novel rigorous mathematical formulation of the variational objective in function spaces for training. VANO first maps an input function to a distribution over a latent space using a parametric encoder and then decodes a sample from the latent distribution to reconstruct the input, as in classic variational autoencoders. We test VANO with different model set-ups and architecture choices for a variety of benchmarks. We start from a simple Gaussian random field where we can analytically track what the model learns and progressively transition to more challenging benchmarks including modeling phase separation in Cahn-Hilliard systems and real world satellite data for measuring Earth surface deformation.

Scalable Bayesian optimization with high-dimensional outputs using randomized prior networks

Several fundamental problems in science and engineering consist of global optimization tasks involving unknown high-dimensional (black-box) functions that map a set of controllable variables to the outcomes of an expensive experiment. Bayesian Optimization (BO) techniques are known to be effective in tackling global optimization problems using a relatively small number objective function evaluations, but their performance suffers when dealing with high-dimensional outputs. To overcome the major challenge of dimensionality, here we propose a deep learning framework for BO and sequential decision making based on bootstrapped ensembles of neural architectures with randomized priors. Using appropriate architecture choices, we show that the proposed framework can approximate functional relationships between design variables and quantities of interest, even in cases where the latter take values in high-dimensional vector spaces or even infinite-dimensional function spaces. In the context of BO, we augmented the proposed probabilistic surrogates with re-parameterized Monte Carlo approximations of multiple-point (parallel) acquisition functions, as well as methodological extensions for accommodating black-box constraints and multi-fidelity information sources. We test the proposed framework against state-of-the-art methods for BO and demonstrate superior performance across several challenging tasks with high-dimensional outputs, including a constrained optimization task involving shape optimization of rotor blades in turbo-machinery.

Random Weight Factorization Improves the Training of Continuous Neural Representations

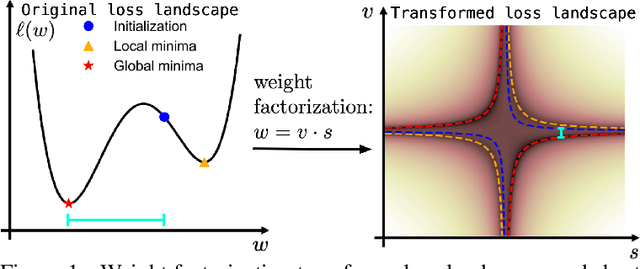
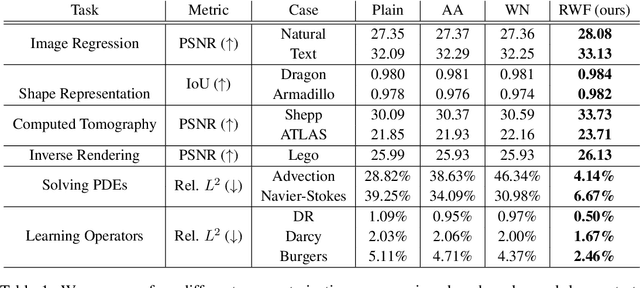
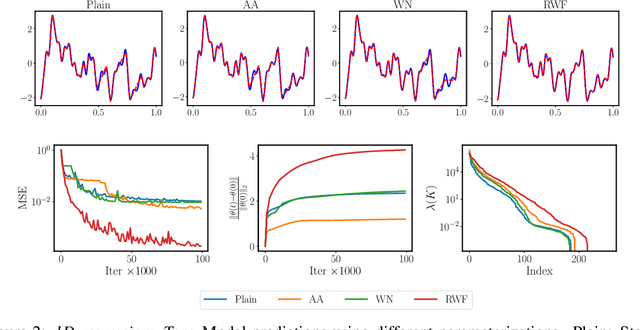
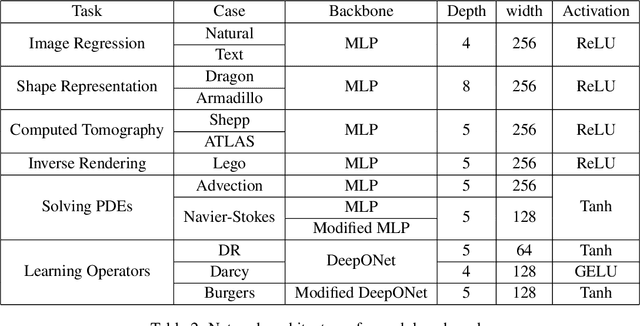
Continuous neural representations have recently emerged as a powerful and flexible alternative to classical discretized representations of signals. However, training them to capture fine details in multi-scale signals is difficult and computationally expensive. Here we propose random weight factorization as a simple drop-in replacement for parameterizing and initializing conventional linear layers in coordinate-based multi-layer perceptrons (MLPs) that significantly accelerates and improves their training. We show how this factorization alters the underlying loss landscape and effectively enables each neuron in the network to learn using its own self-adaptive learning rate. This not only helps with mitigating spectral bias, but also allows networks to quickly recover from poor initializations and reach better local minima. We demonstrate how random weight factorization can be leveraged to improve the training of neural representations on a variety of tasks, including image regression, shape representation, computed tomography, inverse rendering, solving partial differential equations, and learning operators between function spaces.

$Δ$-PINNs: physics-informed neural networks on complex geometries

Physics-informed neural networks (PINNs) have demonstrated promise in solving forward and inverse problems involving partial differential equations. Despite recent progress on expanding the class of problems that can be tackled by PINNs, most of existing use-cases involve simple geometric domains. To date, there is no clear way to inform PINNs about the topology of the domain where the problem is being solved. In this work, we propose a novel positional encoding mechanism for PINNs based on the eigenfunctions of the Laplace-Beltrami operator. This technique allows to create an input space for the neural network that represents the geometry of a given object. We approximate the eigenfunctions as well as the operators involved in the partial differential equations with finite elements. We extensively test and compare the proposed methodology against traditional PINNs in complex shapes, such as a coil, a heat sink and a bunny, with different physics, such as the Eikonal equation and heat transfer. We also study the sensitivity of our method to the number of eigenfunctions used, as well as the discretization used for the eigenfunctions and the underlying operators. Our results show excellent agreement with the ground truth data in cases where traditional PINNs fail to produce a meaningful solution. We envision this new technique will expand the effectiveness of PINNs to more realistic applications.