MINERVA: Evaluating Complex Video Reasoning

Multimodal LLMs are turning their focus to video benchmarks, however most video benchmarks only provide outcome supervision, with no intermediate or interpretable reasoning steps. This makes it challenging to assess if models are truly able to combine perceptual and temporal information to reason about videos, or simply get the correct answer by chance or by exploiting linguistic biases. To remedy this, we provide a new video reasoning dataset called MINERVA for modern multimodal models. Each question in the dataset comes with 5 answer choices, as well as detailed, hand-crafted reasoning traces. Our dataset is multimodal, diverse in terms of video domain and length, and consists of complex multi-step questions. Extensive benchmarking shows that our dataset provides a challenge for frontier open-source and proprietary models. We perform fine-grained error analysis to identify common failure modes across various models, and create a taxonomy of reasoning errors. We use this to explore both human and LLM-as-a-judge methods for scoring video reasoning traces, and find that failure modes are primarily related to temporal localization, followed by visual perception errors, as opposed to logical or completeness errors. The dataset, along with questions, answer candidates and reasoning traces will be publicly available under https://github.com/google-deepmind/neptune?tab=readme-ov-file\#minerva.

Neptune: The Long Orbit to Benchmarking Long Video Understanding

This paper describes a semi-automatic pipeline to generate challenging question-answer-decoy sets for understanding long videos. Many existing video datasets and models are focused on short clips (10s-30s). While some long video datasets do exist, they can often be solved by powerful image models applied per frame (and often to very few frames) in a video, and are usually manually annotated at high cost. In order to mitigate both these problems, we propose a scalable dataset creation pipeline which leverages large models (VLMs and LLMs), to automatically generate dense, time-aligned video captions, as well as tough question answer decoy sets for video segments (up to 15 minutes in length). Our dataset Neptune covers a broad range of long video reasoning abilities and consists of a subset that emphasizes multimodal reasoning. Since existing metrics for open-ended question answering are either rule-based or may rely on proprietary models, we provide a new open source model-based metric GEM to score open-ended responses on Neptune. Benchmark evaluations reveal that most current open-source long video models perform poorly on Neptune, particularly on questions testing temporal ordering, counting and state changes. Through Neptune, we aim to spur the development of more advanced models capable of understanding long videos. The dataset is available at https://github.com/google-deepmind/neptune

Fashion Retail: Forecasting Demand for New Items

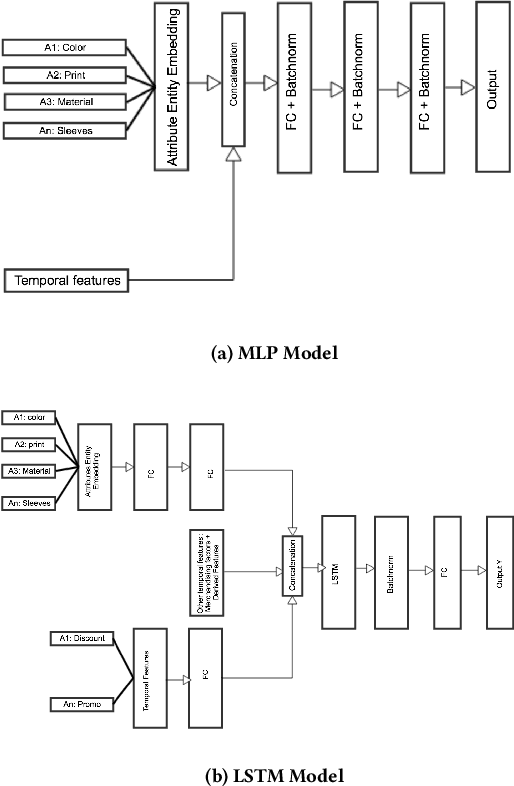
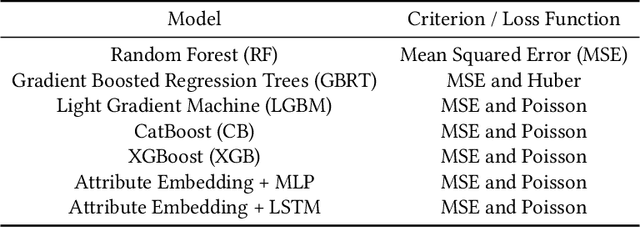
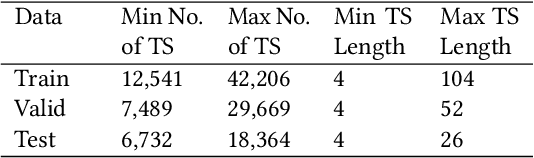
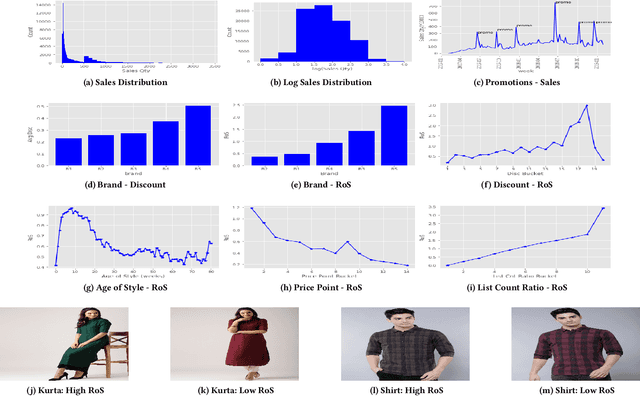
Fashion merchandising is one of the most complicated problems in forecasting, given the transient nature of trends in colours, prints, cuts, patterns, and materials in fashion, the economies of scale achievable only in bulk production, as well as geographical variations in consumption. Retailers that serve a large customer base spend a lot of money and resources to stay prepared for meeting changing fashion demands, and incur huge losses in unsold inventory and liquidation costs [2]. This problem has been addressed by analysts and statisticians as well as ML researchers in a conventional fashion - of building models that forecast for future demand given a particular item of fashion with historical data on its sales. To our knowledge, none of these models have generalized well to predict future demand at an abstracted level for a new design/style of fashion article. To address this problem, we present a study of large scale fashion sales data and directly infer which clothing/footwear attributes and merchandising factors drove demand for those items. We then build generalised models to forecast demand given new item attributes, and demonstrate robust performance by experimenting with different neural architectures, ML methods, and loss functions.