Graphon Estimation in bipartite graphs with observable edge labels and unobservable node labels

Many real-world data sets can be presented in the form of a matrix whose entries correspond to the interaction between two entities of different natures (number of times a web user visits a web page, a student's grade in a subject, a patient's rating of a doctor, etc.). We assume in this paper that the mentioned interaction is determined by unobservable latent variables describing each entity. Our objective is to estimate the conditional expectation of the data matrix given the unobservable variables. This is presented as a problem of estimation of a bivariate function referred to as graphon. We study the cases of piecewise constant and H\"older-continuous graphons. We establish finite sample risk bounds for the least squares estimator and the exponentially weighted aggregate. These bounds highlight the dependence of the estimation error on the size of the data set, the maximum intensity of the interactions, and the level of noise. As the analyzed least-squares estimator is intractable, we propose an adaptation of Lloyd's alternating minimization algorithm to compute an approximation of the least-squares estimator. Finally, we present numerical experiments in order to illustrate the empirical performance of the graphon estimator on synthetic data sets.

Nearly minimax robust estimator of the mean vector by iterative spectral dimension reduction

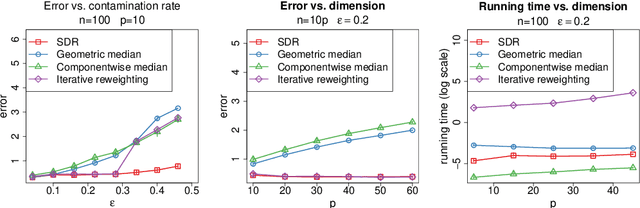
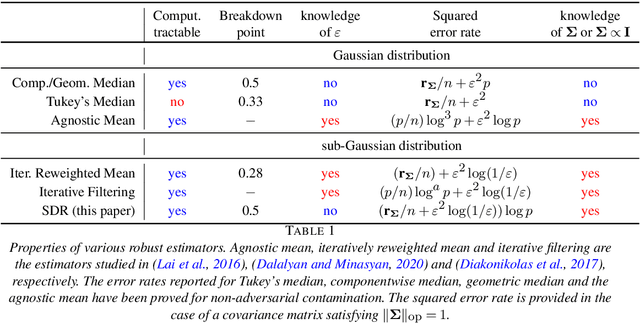
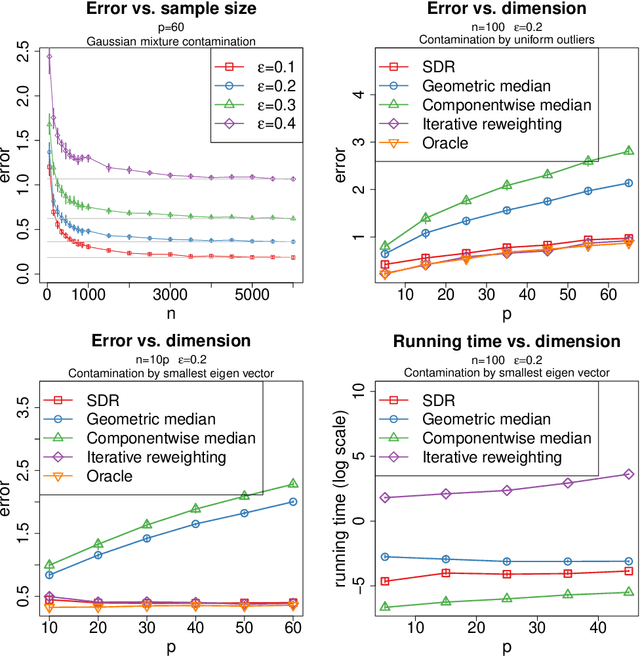
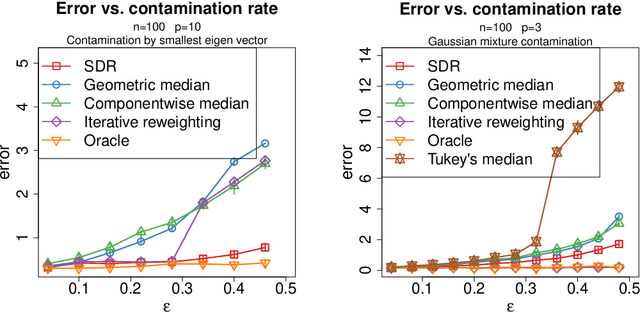
We study the problem of robust estimation of the mean vector of a sub-Gaussian distribution. We introduce an estimator based on spectral dimension reduction (SDR) and establish a finite sample upper bound on its error that is minimax-optimal up to a logarithmic factor. Furthermore, we prove that the breakdown point of the SDR estimator is equal to $1/2$, the highest possible value of the breakdown point. In addition, the SDR estimator is equivariant by similarity transforms and has low computational complexity. More precisely, in the case of $n$ vectors of dimension $p$ -- at most $\varepsilon n$ out of which are adversarially corrupted -- the SDR estimator has a squared error of order $\big(\frac{r_\Sigma}{n} + \varepsilon^2\log(1/\varepsilon)\big){\log p}$ and a running time of order $p^3 + n p^2$. Here, $r_\Sigma\le p$ is the effective rank of the covariance matrix of the reference distribution. Another advantage of the SDR estimator is that it does not require knowledge of the contamination rate and does not involve sample splitting. We also investigate extensions of the proposed algorithm and of the obtained results in the case of (partially) unknown covariance matrix.

Penalized Langevin dynamics with vanishing penalty for smooth and log-concave targets

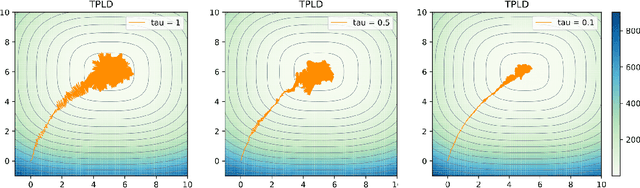
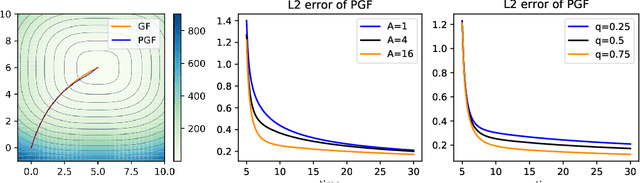
We study the problem of sampling from a probability distribution on $\mathbb R^p$ defined via a convex and smooth potential function. We consider a continuous-time diffusion-type process, termed Penalized Langevin dynamics (PLD), the drift of which is the negative gradient of the potential plus a linear penalty that vanishes when time goes to infinity. An upper bound on the Wasserstein-2 distance between the distribution of the PLD at time $t$ and the target is established. This upper bound highlights the influence of the speed of decay of the penalty on the accuracy of the approximation. As a consequence, considering the low-temperature limit we infer a new nonasymptotic guarantee of convergence of the penalized gradient flow for the optimization problem.

Bounding the error of discretized Langevin algorithms for non-strongly log-concave targets

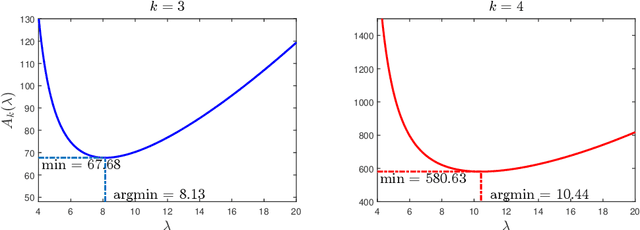
In this paper, we provide non-asymptotic upper bounds on the error of sampling from a target density using three schemes of discretized Langevin diffusions. The first scheme is the Langevin Monte Carlo (LMC) algorithm, the Euler discretization of the Langevin diffusion. The second and the third schemes are, respectively, the kinetic Langevin Monte Carlo (KLMC) for differentiable potentials and the kinetic Langevin Monte Carlo for twice-differentiable potentials (KLMC2). The main focus is on the target densities that are smooth and log-concave on $\RR^p$, but not necessarily strongly log-concave. Bounds on the computational complexity are obtained under two types of smoothness assumption: the potential has a Lipschitz-continuous gradient and the potential has a Lipschitz-continuous Hessian matrix. The error of sampling is measured by Wasserstein-$q$ distances and the bounded-Lipschitz distance. We advocate for the use of a new dimension-adapted scaling in the definition of the computational complexity, when Wasserstein-$q$ distances are considered. The obtained results show that the number of iterations to achieve a scaled-error smaller than a prescribed value depends only polynomially in the dimension.

Outlier-robust estimation of a sparse linear model using $\ell_1$-penalized Huber's $M$-estimator

We study the problem of estimating a $p$-dimensional $s$-sparse vector in a linear model with Gaussian design and additive noise. In the case where the labels are contaminated by at most $o$ adversarial outliers, we prove that the $\ell_1$-penalized Huber's $M$-estimator based on $n$ samples attains the optimal rate of convergence $(s/n)^{1/2} + (o/n)$, up to a logarithmic factor. For more general design matrices, our results highlight the importance of two properties: the transfer principle and the incoherence property. These properties with suitable constants are shown to yield the optimal rates, up to log-factors, of robust estimation with adversarial contamination.

A nonasymptotic law of iterated logarithm for robust online estimators

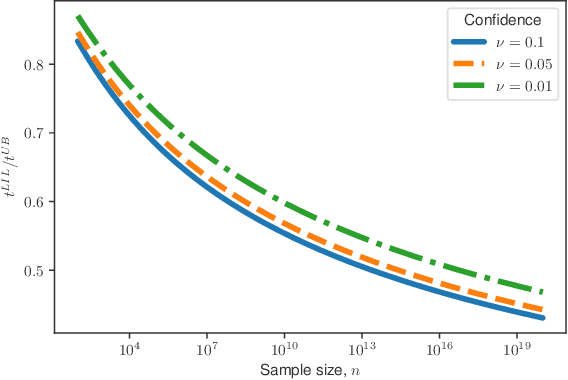
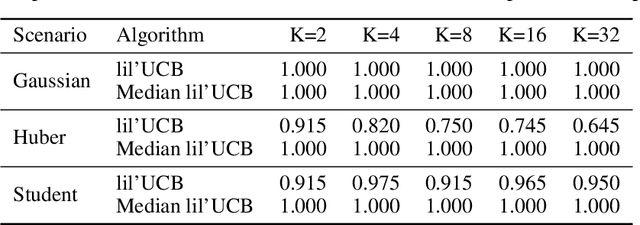
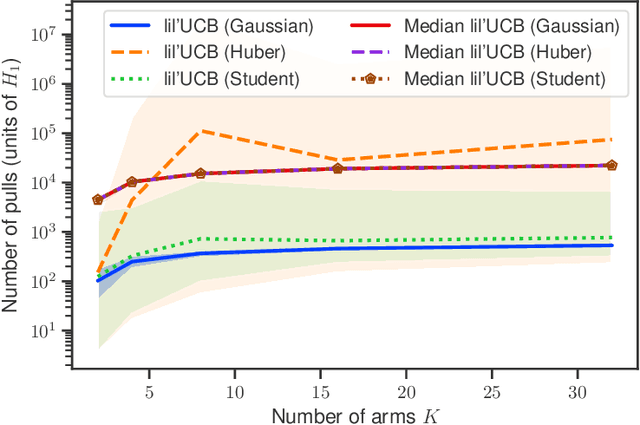
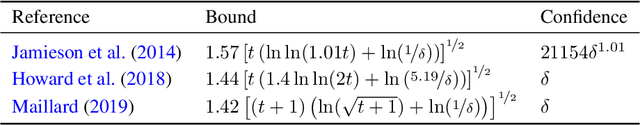
In this paper, we provide tight deviation bounds for M-estimators, which are valid with a prescribed probability for every sample size. M-estimators are ubiquitous in machine learning and statistical learning theory. They are used both for defining prediction strategies and for evaluating their precision. Our deviation bounds can be seen as a non-asymptotic version of the law of iterated logarithm. They are established under general assumptions such as Lipschitz continuity of the loss function and (local) curvature of the population risk. These conditions are satisfied for most examples used in machine learning, including those that are known to be robust to outliers and to heavy tailed distributions. To further highlight the scope of applicability of the obtained results, a new algorithm, with provably optimal theoretical guarantees, for the best arm identification in a stochastic multi-arm bandit setting is presented. Numerical experiments illustrating the validity of the algorithm are reported.

Minimax rates in outlier-robust estimation of discrete models

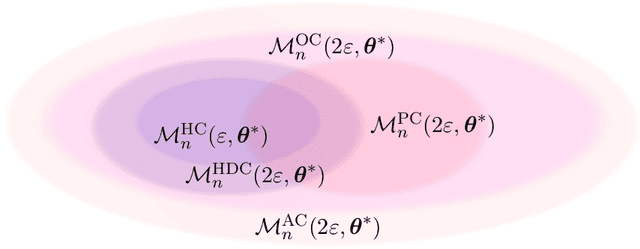
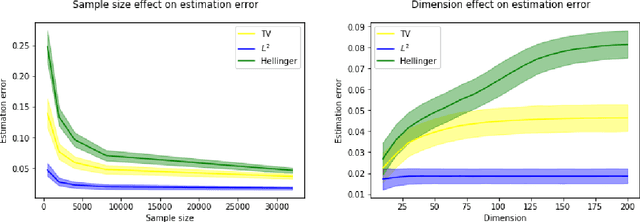
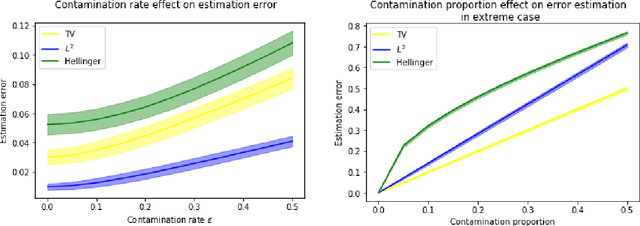
We consider the problem of estimating the probability distribution of a discrete random variable in the setting where the observations are corrupted by outliers. Assuming that the discrete variable takes k values, the unknown parameter p is a k-dimensional vector belonging to the probability simplex. We first describe various settings of contamination and discuss the relation between these settings. We then establish minimax rates when the quality of estimation is measured by the total-variation distance, the Hellinger distance, or the L2-distance between two probability measures. Our analysis reveals that the minimax rates associated to these three distances are all different, but they are all attained by the maximum likelihood estimator. Note that the latter is efficiently computable even when the dimension is large. Some numerical experiments illustrating our theoretical findings are reported.

On sampling from a log-concave density using kinetic Langevin diffusions

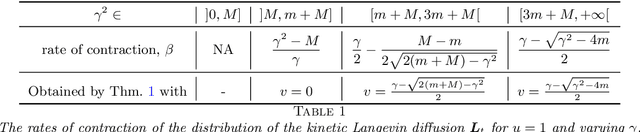
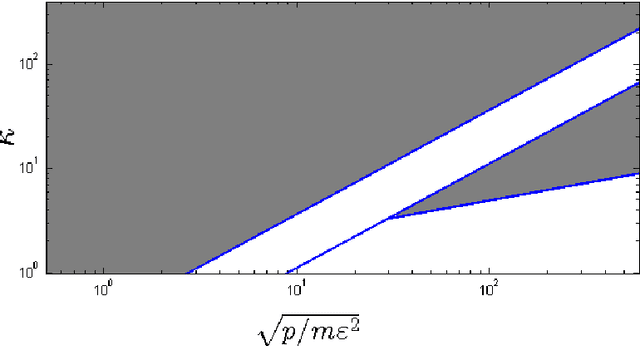
Langevin diffusion processes and their discretizations are often used for sampling from a target density. The most convenient framework for assessing the quality of such a sampling scheme corresponds to smooth and strongly log-concave densities defined on $\mathbb R^p$. The present work focuses on this framework and studies the behavior of Monte Carlo algorithms based on discretizations of the kinetic Langevin diffusion. We first prove the geometric mixing property of the kinetic Langevin diffusion with a mixing rate that is, in the overdamped regime, optimal in terms of its dependence on the condition number. We then use this result for obtaining improved guarantees of sampling using the kinetic Langevin Monte Carlo method, when the quality of sampling is measured by the Wasserstein distance. We also consider the situation where the Hessian of the log-density of the target distribution is Lipschitz-continuous. In this case, we introduce a new discretization of the kinetic Langevin diffusion and prove that this leads to a substantial improvement of the upper bound on the sampling error measured in Wasserstein distance.

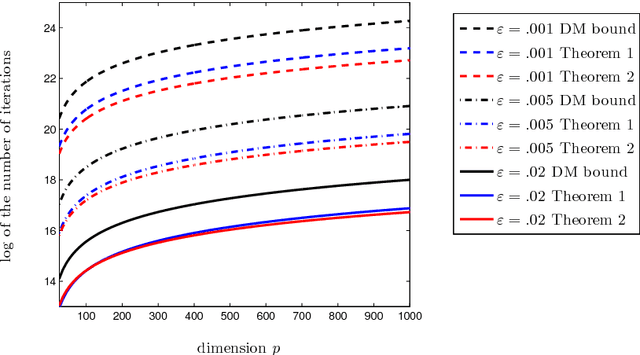
User-friendly guarantees for the Langevin Monte Carlo with inaccurate gradient

In this paper, we study the problem of sampling from a given probability density function that is known to be smooth and strongly log-concave. We analyze several methods of approximate sampling based on discretizations of the (highly overdamped) Langevin diffusion and establish guarantees on its error measured in the Wasserstein-2 distance. Our guarantees improve or extend the state-of-the-art results in three directions. First, we provide an upper bound on the error of the first-order Langevin Monte Carlo (LMC) algorithm with optimized varying step-size. This result has the advantage of being horizon free (we do not need to know in advance the target precision) and to improve by a logarithmic factor the corresponding result for the constant step-size. Second, we study the case where accurate evaluations of the gradient of the log-density are unavailable, but one can have access to approximations of the aforementioned gradient. In such a situation, we consider both deterministic and stochastic approximations of the gradient and provide an upper bound on the sampling error of the first-order LMC that quantifies the impact of the gradient evaluation inaccuracies. Third, we establish upper bounds for two versions of the second-order LMC, which leverage the Hessian of the log-density. We nonasymptotic guarantees on the sampling error of these second-order LMCs. These guarantees reveal that the second-order LMC algorithms improve on the first-order LMC in ill-conditioned settings.

Theoretical guarantees for approximate sampling from smooth and log-concave densities

Sampling from various kinds of distributions is an issue of paramount importance in statistics since it is often the key ingredient for constructing estimators, test procedures or confidence intervals. In many situations, the exact sampling from a given distribution is impossible or computationally expensive and, therefore, one needs to resort to approximate sampling strategies. However, there is no well-developed theory providing meaningful nonasymptotic guarantees for the approximate sampling procedures, especially in the high-dimensional problems. This paper makes some progress in this direction by considering the problem of sampling from a distribution having a smooth and log-concave density defined on \(\RR^p\), for some integer \(p>0\). We establish nonasymptotic bounds for the error of approximating the target distribution by the one obtained by the Langevin Monte Carlo method and its variants. We illustrate the effectiveness of the established guarantees with various experiments. Underlying our analysis are insights from the theory of continuous-time diffusion processes, which may be of interest beyond the framework of log-concave densities considered in the present work.