An example of prediction which complies with Demographic Parity and equalizes group-wise risks in the context of regression
Paper and Code
Nov 13, 2020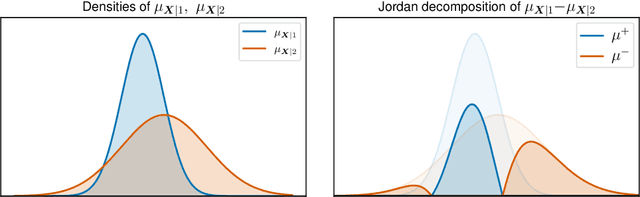
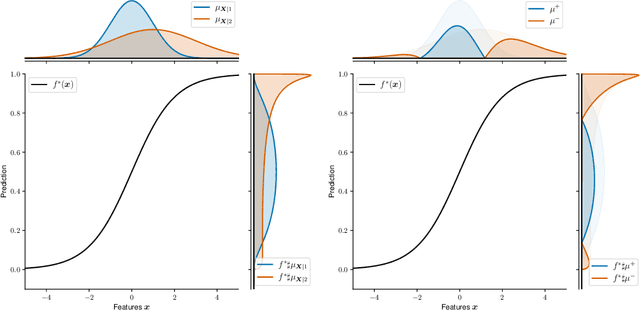
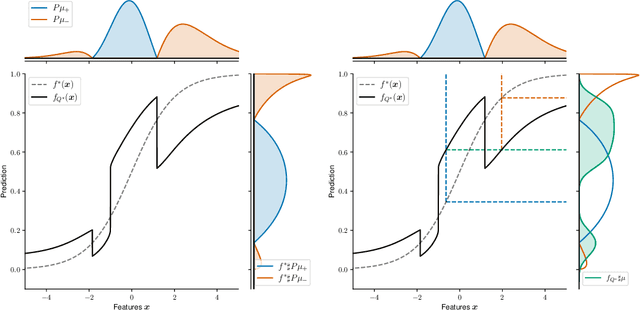
Let $(X, S, Y) \in \mathbb{R}^p \times \{1, 2\} \times \mathbb{R}$ be a triplet following some joint distribution $\mathbb{P}$ with feature vector $X$, sensitive attribute $S$ , and target variable $Y$. The Bayes optimal prediction $f^*$ which does not produce Disparate Treatment is defined as $f^*(x) = \mathbb{E}[Y | X = x]$. We provide a non-trivial example of a prediction $x \to f(x)$ which satisfies two common group-fairness notions: Demographic Parity \begin{align} (f(X) | S = 1) &\stackrel{d}{=} (f(X) | S = 2) \end{align} and Equal Group-Wise Risks \begin{align} \mathbb{E}[(f^*(X) - f(X))^2 | S = 1] = \mathbb{E}[(f^*(X) - f(X))^2 | S = 2]. \end{align} To the best of our knowledge this is the first explicit construction of a non-constant predictor satisfying the above. We discuss several implications of this result on better understanding of mathematical notions of algorithmic fairness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge