SALUDA: Surface-based Automotive Lidar Unsupervised Domain Adaptation

Learning models on one labeled dataset that generalize well on another domain is a difficult task, as several shifts might happen between the data domains. This is notably the case for lidar data, for which models can exhibit large performance discrepancies due for instance to different lidar patterns or changes in acquisition conditions. This paper addresses the corresponding Unsupervised Domain Adaptation (UDA) task for semantic segmentation. To mitigate this problem, we introduce an unsupervised auxiliary task of learning an implicit underlying surface representation simultaneously on source and target data. As both domains share the same latent representation, the model is forced to accommodate discrepancies between the two sources of data. This novel strategy differs from classical minimization of statistical divergences or lidar-specific state-of-the-art domain adaptation techniques. Our experiments demonstrate that our method achieves a better performance than the current state of the art in synthetic-to-real and real-to-real scenarios.

Sliced-Wasserstein on Symmetric Positive Definite Matrices for M/EEG Signals

When dealing with electro or magnetoencephalography records, many supervised prediction tasks are solved by working with covariance matrices to summarize the signals. Learning with these matrices requires using Riemanian geometry to account for their structure. In this paper, we propose a new method to deal with distributions of covariance matrices and demonstrate its computational efficiency on M/EEG multivariate time series. More specifically, we define a Sliced-Wasserstein distance between measures of symmetric positive definite matrices that comes with strong theoretical guarantees. Then, we take advantage of its properties and kernel methods to apply this distance to brain-age prediction from MEG data and compare it to state-of-the-art algorithms based on Riemannian geometry. Finally, we show that it is an efficient surrogate to the Wasserstein distance in domain adaptation for Brain Computer Interface applications.

Hyperbolic Sliced-Wasserstein via Geodesic and Horospherical Projections

It has been shown beneficial for many types of data which present an underlying hierarchical structure to be embedded in hyperbolic spaces. Consequently, many tools of machine learning were extended to such spaces, but only few discrepancies to compare probability distributions defined over those spaces exist. Among the possible candidates, optimal transport distances are well defined on such Riemannian manifolds and enjoy strong theoretical properties, but suffer from high computational cost. On Euclidean spaces, sliced-Wasserstein distances, which leverage a closed-form of the Wasserstein distance in one dimension, are more computationally efficient, but are not readily available on hyperbolic spaces. In this work, we propose to derive novel hyperbolic sliced-Wasserstein discrepancies. These constructions use projections on the underlying geodesics either along horospheres or geodesics. We study and compare them on different tasks where hyperbolic representations are relevant, such as sampling or image classification.

Turning Normalizing Flows into Monge Maps with Geodesic Gaussian Preserving Flows

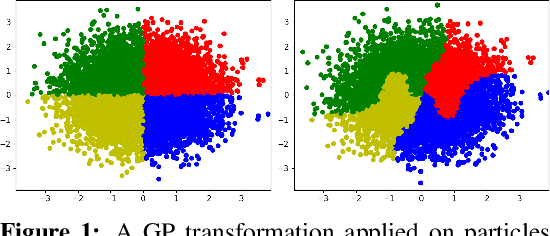
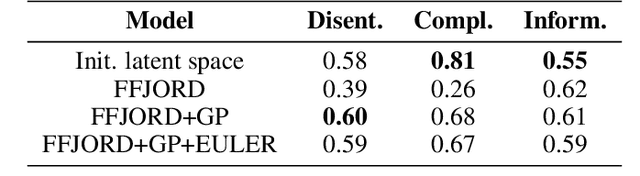
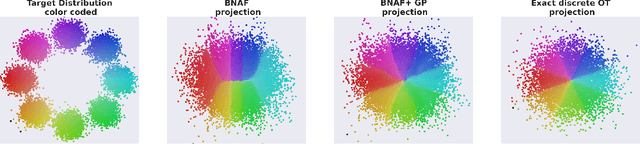
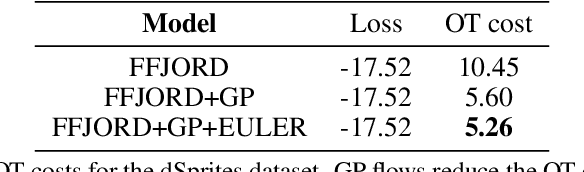
Normalizing Flows (NF) are powerful likelihood-based generative models that are able to trade off between expressivity and tractability to model complex densities. A now well established research avenue leverages optimal transport (OT) and looks for Monge maps, i.e. models with minimal effort between the source and target distributions. This paper introduces a method based on Brenier's polar factorization theorem to transform any trained NF into a more OT-efficient version without changing the final density. We do so by learning a rearrangement of the source (Gaussian) distribution that minimizes the OT cost between the source and the final density. We further constrain the path leading to the estimated Monge map to lie on a geodesic in the space of volume-preserving diffeomorphisms thanks to Euler's equations. The proposed method leads to smooth flows with reduced OT cost for several existing models without affecting the model performance.

Aligning individual brains with Fused Unbalanced Gromov-Wasserstein

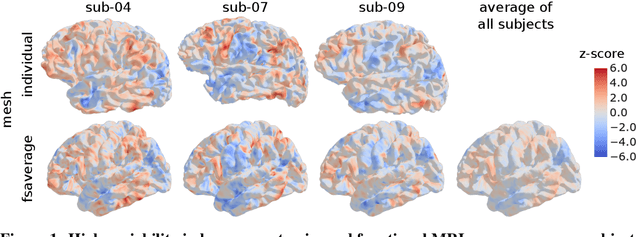
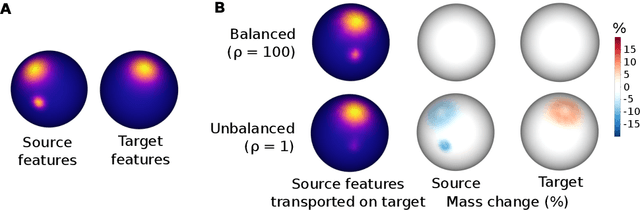
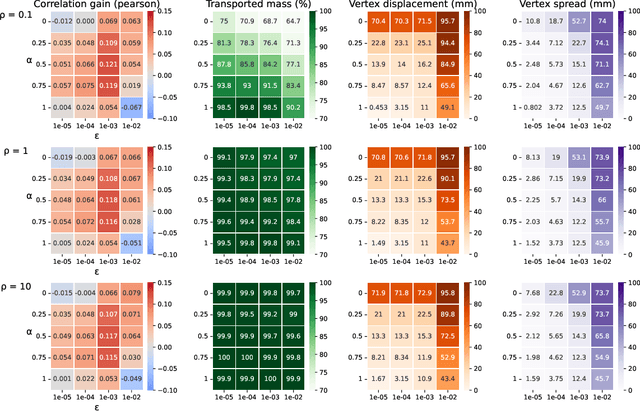
Individual brains vary in both anatomy and functional organization, even within a given species. Inter-individual variability is a major impediment when trying to draw generalizable conclusions from neuroimaging data collected on groups of subjects. Current co-registration procedures rely on limited data, and thus lead to very coarse inter-subject alignments. In this work, we present a novel method for inter-subject alignment based on Optimal Transport, denoted as Fused Unbalanced Gromov Wasserstein (FUGW). The method aligns cortical surfaces based on the similarity of their functional signatures in response to a variety of stimulation settings, while penalizing large deformations of individual topographic organization. We demonstrate that FUGW is well-suited for whole-brain landmark-free alignment. The unbalanced feature allows to deal with the fact that functional areas vary in size across subjects. Our results show that FUGW alignment significantly increases between-subject correlation of activity for independent functional data, and leads to more precise mapping at the group level.

Spherical Sliced-Wasserstein

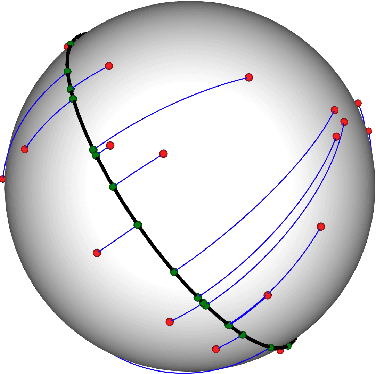
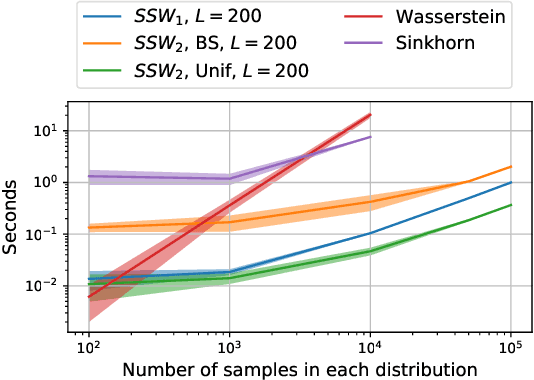
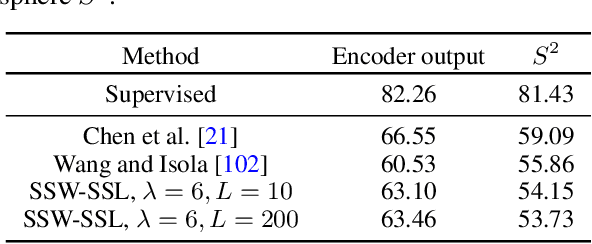
Many variants of the Wasserstein distance have been introduced to reduce its original computational burden. In particular the Sliced-Wasserstein distance (SW), which leverages one-dimensional projections for which a closed-form solution of the Wasserstein distance is available, has received a lot of interest. Yet, it is restricted to data living in Euclidean spaces, while the Wasserstein distance has been studied and used recently on manifolds. We focus more specifically on the sphere, for which we define a novel SW discrepancy, which we call spherical Sliced-Wasserstein, making a first step towards defining SW discrepancies on manifolds. Our construction is notably based on closed-form solutions of the Wasserstein distance on the circle, together with a new spherical Radon transform. Along with efficient algorithms and the corresponding implementations, we illustrate its properties in several machine learning use cases where spherical representations of data are at stake: density estimation on the sphere, variational inference or hyperspherical auto-encoders.

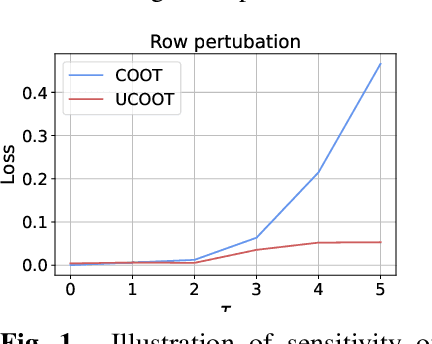
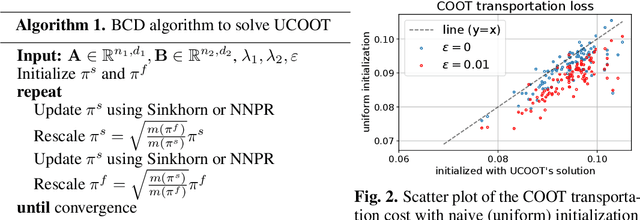
Unbalanced CO-Optimal Transport

Optimal transport (OT) compares probability distributions by computing a meaningful alignment between their samples. CO-optimal transport (COOT) takes this comparison further by inferring an alignment between features as well. While this approach leads to better alignments and generalizes both OT and Gromov-Wasserstein distances, we provide a theoretical result showing that it is sensitive to outliers that are omnipresent in real-world data. This prompts us to propose unbalanced COOT for which we provably show its robustness to noise in the compared datasets. To the best of our knowledge, this is the first such result for OT methods in incomparable spaces. With this result in hand, we provide empirical evidence of this robustness for the challenging tasks of heterogeneous domain adaptation with and without varying proportions of classes and simultaneous alignment of samples and features across single-cell measurements.

Template based Graph Neural Network with Optimal Transport Distances

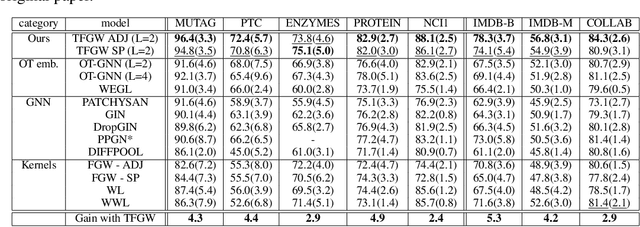
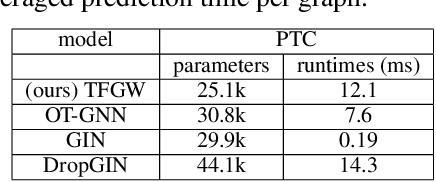
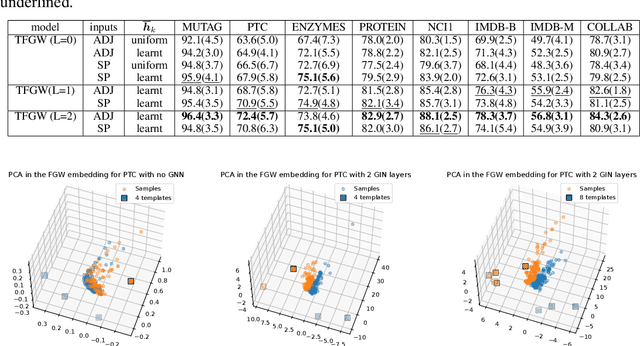
Current Graph Neural Networks (GNN) architectures generally rely on two important components: node features embedding through message passing, and aggregation with a specialized form of pooling. The structural (or topological) information is implicitly taken into account in these two steps. We propose in this work a novel point of view, which places distances to some learnable graph templates at the core of the graph representation. This distance embedding is constructed thanks to an optimal transport distance: the Fused Gromov-Wasserstein (FGW) distance, which encodes simultaneously feature and structure dissimilarities by solving a soft graph-matching problem. We postulate that the vector of FGW distances to a set of template graphs has a strong discriminative power, which is then fed to a non-linear classifier for final predictions. Distance embedding can be seen as a new layer, and can leverage on existing message passing techniques to promote sensible feature representations. Interestingly enough, in our work the optimal set of template graphs is also learnt in an end-to-end fashion by differentiating through this layer. After describing the corresponding learning procedure, we empirically validate our claim on several synthetic and real life graph classification datasets, where our method is competitive or surpasses kernel and GNN state-of-the-art approaches. We complete our experiments by an ablation study and a sensitivity analysis to parameters.

Metric Learning-enhanced Optimal Transport for Biochemical Regression Domain Adaptation

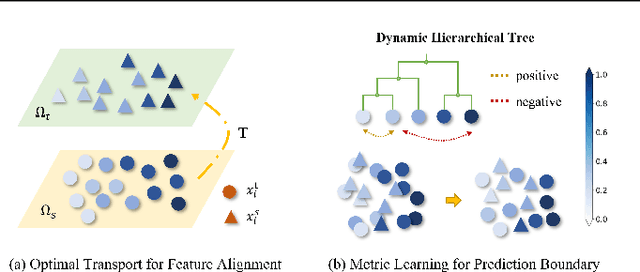
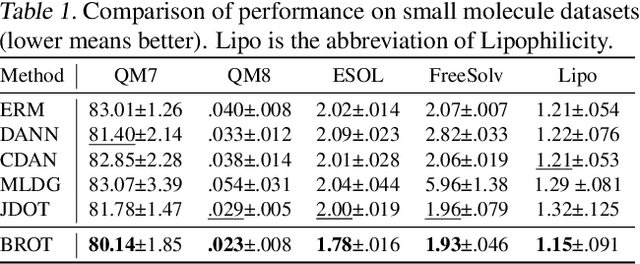
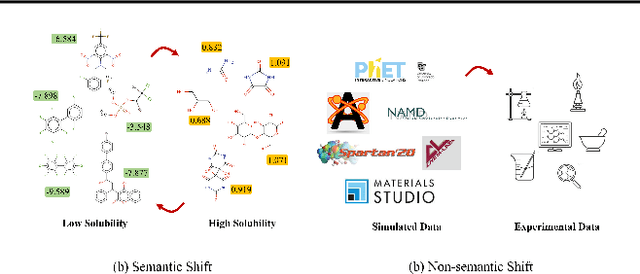
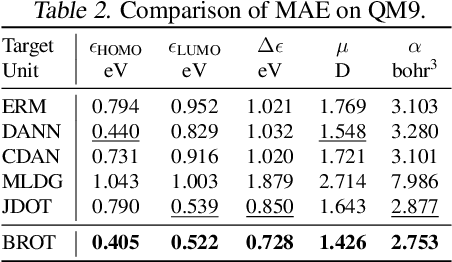
Generalizing knowledge beyond source domains is a crucial prerequisite for many biomedical applications such as drug design and molecular property prediction. To meet this challenge, researchers have used optimal transport (OT) to perform representation alignment between the source and target domains. Yet existing OT algorithms are mainly designed for classification tasks. Accordingly, we consider regression tasks in the unsupervised and semi-supervised settings in this paper. To exploit continuous labels, we propose novel metrics to measure domain distances and introduce a posterior variance regularizer on the transport plan. Further, while computationally appealing, OT suffers from ambiguous decision boundaries and biased local data distributions brought by the mini-batch training. To address those issues, we propose to couple OT with metric learning to yield more robust boundaries and reduce bias. Specifically, we present a dynamic hierarchical triplet loss to describe the global data distribution, where the cluster centroids are progressively adjusted among consecutive iterations. We evaluate our method on both unsupervised and semi-supervised learning tasks in biochemistry. Experiments show the proposed method significantly outperforms state-of-the-art baselines across various benchmark datasets of small molecules and material crystals.

Sliced-Wasserstein Gradient Flows

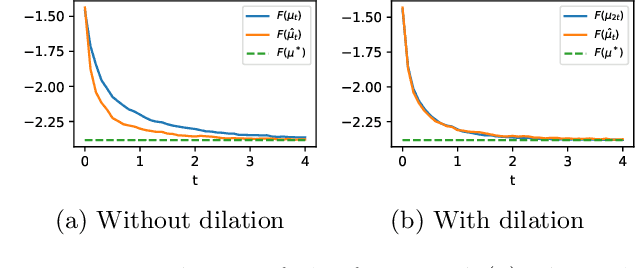
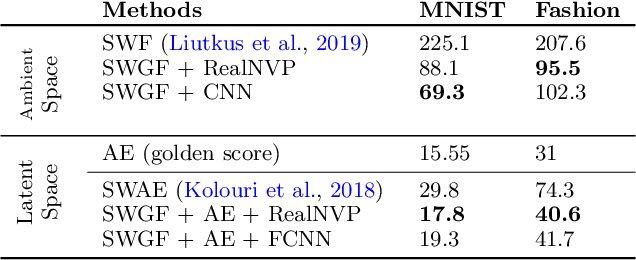
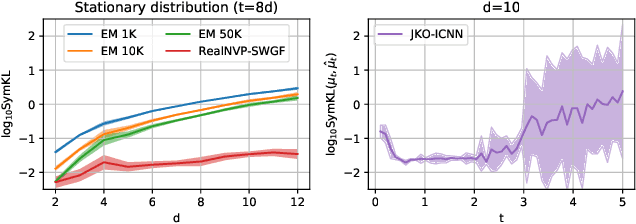
Minimizing functionals in the space of probability distributions can be done with Wasserstein gradient flows. To solve them numerically, a possible approach is to rely on the Jordan-Kinderlehrer-Otto (JKO) scheme which is analogous to the proximal scheme in Euclidean spaces. However, this bilevel optimization problem is known for its computational challenges, especially in high dimension. To alleviate it, very recent works propose to approximate the JKO scheme leveraging Brenier's theorem, and using gradients of Input Convex Neural Networks to parameterize the density (JKO-ICNN). However, this method comes with a high computational cost and stability issues. Instead, this work proposes to use gradient flows in the space of probability measures endowed with the sliced-Wasserstein (SW) distance. We argue that this method is more flexible than JKO-ICNN, since SW enjoys a closed-form differentiable approximation. Thus, the density at each step can be parameterized by any generative model which alleviates the computational burden and makes it tractable in higher dimensions. Interestingly, we also show empirically that these gradient flows are strongly related to the usual Wasserstein gradient flows, and that they can be used to minimize efficiently diverse machine learning functionals.