Online Linear Regression with Paid Stochastic Features

We study an online linear regression setting in which the observed feature vectors are corrupted by noise and the learner can pay to reduce the noise level. In practice, this may happen for several reasons: for example, because features can be measured more accurately using more expensive equipment, or because data providers can be incentivized to release less private features. Assuming feature vectors are drawn i.i.d. from a fixed but unknown distribution, we measure the learner's regret against the linear predictor minimizing a notion of loss that combines the prediction error and payment. When the mapping between payments and noise covariance is known, we prove that the rate $\sqrt{T}$ is optimal for regret if logarithmic factors are ignored. When the noise covariance is unknown, we show that the optimal regret rate becomes of order $T^{2/3}$ (ignoring log factors). Our analysis leverages matrix martingale concentration, showing that the empirical loss uniformly converges to the expected one for all payments and linear predictors.

Instance-Dependent Regret Bounds for Nonstochastic Linear Partial Monitoring

In contrast to the classic formulation of partial monitoring, linear partial monitoring can model infinite outcome spaces, while imposing a linear structure on both the losses and the observations. This setting can be viewed as a generalization of linear bandits where loss and feedback are decoupled in a flexible manner. In this work, we address a nonstochastic (adversarial), finite-actions version of the problem through a simple instance of the exploration-by-optimization method that is amenable to efficient implementation. We derive regret bounds that depend on the game structure in a more transparent manner than previous theoretical guarantees for this paradigm. Our bounds feature instance-specific quantities that reflect the degree of alignment between observations and losses, and resemble known guarantees in the stochastic setting. Notably, they achieve the standard $\sqrt{T}$ rate in easy (locally observable) games and $T^{2/3}$ in hard (globally observable) games, where $T$ is the time horizon. We instantiate these bounds in a selection of old and new partial information settings subsumed by this model, and illustrate that the achieved dependence on the game structure can be tight in interesting cases.

Of Dice and Games: A Theory of Generalized Boosting

Cost-sensitive loss functions are crucial in many real-world prediction problems, where different types of errors are penalized differently; for example, in medical diagnosis, a false negative prediction can lead to worse consequences than a false positive prediction. However, traditional PAC learning theory has mostly focused on the symmetric 0-1 loss, leaving cost-sensitive losses largely unaddressed. In this work, we extend the celebrated theory of boosting to incorporate both cost-sensitive and multi-objective losses. Cost-sensitive losses assign costs to the entries of a confusion matrix, and are used to control the sum of prediction errors accounting for the cost of each error type. Multi-objective losses, on the other hand, simultaneously track multiple cost-sensitive losses, and are useful when the goal is to satisfy several criteria at once (e.g., minimizing false positives while keeping false negatives below a critical threshold). We develop a comprehensive theory of cost-sensitive and multi-objective boosting, providing a taxonomy of weak learning guarantees that distinguishes which guarantees are trivial (i.e., can always be achieved), which ones are boostable (i.e., imply strong learning), and which ones are intermediate, implying non-trivial yet not arbitrarily accurate learning. For binary classification, we establish a dichotomy: a weak learning guarantee is either trivial or boostable. In the multiclass setting, we describe a more intricate landscape of intermediate weak learning guarantees. Our characterization relies on a geometric interpretation of boosting, revealing a surprising equivalence between cost-sensitive and multi-objective losses.

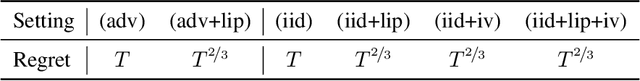
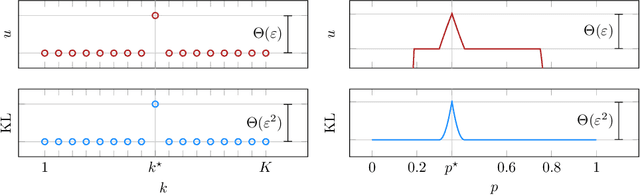
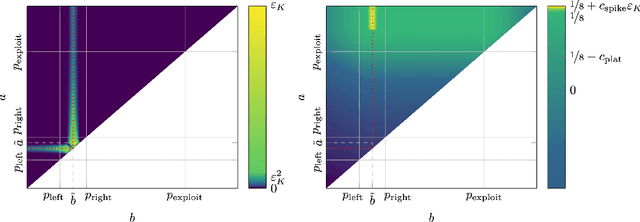
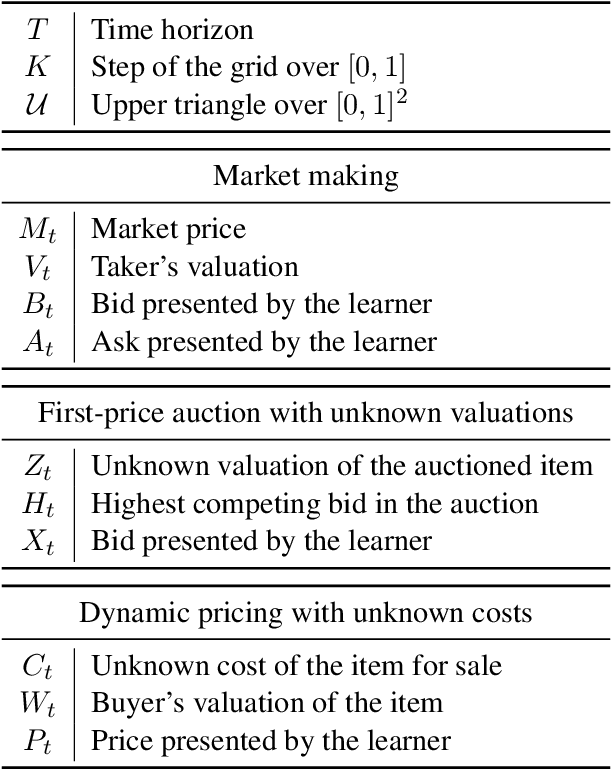
Market Making without Regret

We consider a sequential decision-making setting where, at every round $t$, a market maker posts a bid price $B_t$ and an ask price $A_t$ to an incoming trader (the taker) with a private valuation for one unit of some asset. If the trader's valuation is lower than the bid price, or higher than the ask price, then a trade (sell or buy) occurs. If a trade happens at round $t$, then letting $M_t$ be the market price (observed only at the end of round $t$), the maker's utility is $M_t - B_t$ if the maker bought the asset, and $A_t - M_t$ if they sold it. We characterize the maker's regret with respect to the best fixed choice of bid and ask pairs under a variety of assumptions (adversarial, i.i.d., and their variants) on the sequence of market prices and valuations. Our upper bound analysis unveils an intriguing connection relating market making to first-price auctions and dynamic pricing. Our main technical contribution is a lower bound for the i.i.d. case with Lipschitz distributions and independence between prices and valuations. The difficulty in the analysis stems from the unique structure of the reward and feedback functions, allowing an algorithm to acquire information by graduating the "cost of exploration" in an arbitrary way.

Improved Regret Bounds for Bandits with Expert Advice

In this research note, we revisit the bandits with expert advice problem. Under a restricted feedback model, we prove a lower bound of order $\sqrt{K T \ln(N/K)}$ for the worst-case regret, where $K$ is the number of actions, $N>K$ the number of experts, and $T$ the time horizon. This matches a previously known upper bound of the same order and improves upon the best available lower bound of $\sqrt{K T (\ln N) / (\ln K)}$. For the standard feedback model, we prove a new instance-based upper bound that depends on the agreement between the experts and provides a logarithmic improvement compared to prior results.

A Theory of Interpretable Approximations

Can a deep neural network be approximated by a small decision tree based on simple features? This question and its variants are behind the growing demand for machine learning models that are *interpretable* by humans. In this work we study such questions by introducing *interpretable approximations*, a notion that captures the idea of approximating a target concept $c$ by a small aggregation of concepts from some base class $\mathcal{H}$. In particular, we consider the approximation of a binary concept $c$ by decision trees based on a simple class $\mathcal{H}$ (e.g., of bounded VC dimension), and use the tree depth as a measure of complexity. Our primary contribution is the following remarkable trichotomy. For any given pair of $\mathcal{H}$ and $c$, exactly one of these cases holds: (i) $c$ cannot be approximated by $\mathcal{H}$ with arbitrary accuracy; (ii) $c$ can be approximated by $\mathcal{H}$ with arbitrary accuracy, but there exists no universal rate that bounds the complexity of the approximations as a function of the accuracy; or (iii) there exists a constant $\kappa$ that depends only on $\mathcal{H}$ and $c$ such that, for *any* data distribution and *any* desired accuracy level, $c$ can be approximated by $\mathcal{H}$ with a complexity not exceeding $\kappa$. This taxonomy stands in stark contrast to the landscape of supervised classification, which offers a complex array of distribution-free and universally learnable scenarios. We show that, in the case of interpretable approximations, even a slightly nontrivial a-priori guarantee on the complexity of approximations implies approximations with constant (distribution-free and accuracy-free) complexity. We extend our trichotomy to classes $\mathcal{H}$ of unbounded VC dimension and give characterizations of interpretability based on the algebra generated by $\mathcal{H}$.

Sparsity-Agnostic Linear Bandits with Adaptive Adversaries

We study stochastic linear bandits where, in each round, the learner receives a set of actions (i.e., feature vectors), from which it chooses an element and obtains a stochastic reward. The expected reward is a fixed but unknown linear function of the chosen action. We study sparse regret bounds, that depend on the number $S$ of non-zero coefficients in the linear reward function. Previous works focused on the case where $S$ is known, or the action sets satisfy additional assumptions. In this work, we obtain the first sparse regret bounds that hold when $S$ is unknown and the action sets are adversarially generated. Our techniques combine online to confidence set conversions with a novel randomized model selection approach over a hierarchy of nested confidence sets. When $S$ is known, our analysis recovers state-of-the-art bounds for adversarial action sets. We also show that a variant of our approach, using Exp3 to dynamically select the confidence sets, can be used to improve the empirical performance of stochastic linear bandits while enjoying a regret bound with optimal dependence on the time horizon.

Fair Online Bilateral Trade

In online bilateral trade, a platform posts prices to incoming pairs of buyers and sellers that have private valuations for a certain good. If the price is lower than the buyers' valuation and higher than the sellers' valuation, then a trade takes place. Previous work focused on the platform perspective, with the goal of setting prices maximizing the gain from trade (the sum of sellers' and buyers' utilities). Gain from trade is, however, potentially unfair to traders, as they may receive highly uneven shares of the total utility. In this work we enforce fairness by rewarding the platform with the fair gain from trade, defined as the minimum between sellers' and buyers' utilities. After showing that any no-regret learning algorithm designed to maximize the sum of the utilities may fail badly with fair gain from trade, we present our main contribution: a complete characterization of the regret regimes for fair gain from trade when, after each interaction, the platform only learns whether each trader accepted the current price. Specifically, we prove the following regret bounds: $\Theta(\ln T)$ in the deterministic setting, $\Omega(T)$ in the stochastic setting, and $\tilde{\Theta}(T^{2/3})$ in the stochastic setting when sellers' and buyers' valuations are independent of each other. We conclude by providing tight regret bounds when, after each interaction, the platform is allowed to observe the true traders' valuations.

Information Capacity Regret Bounds for Bandits with Mediator Feedback

This work addresses the mediator feedback problem, a bandit game where the decision set consists of a number of policies, each associated with a probability distribution over a common space of outcomes. Upon choosing a policy, the learner observes an outcome sampled from its distribution and incurs the loss assigned to this outcome in the present round. We introduce the policy set capacity as an information-theoretic measure for the complexity of the policy set. Adopting the classical EXP4 algorithm, we provide new regret bounds depending on the policy set capacity in both the adversarial and the stochastic settings. For a selection of policy set families, we prove nearly-matching lower bounds, scaling similarly with the capacity. We also consider the case when the policies' distributions can vary between rounds, thus addressing the related bandits with expert advice problem, which we improve upon its prior results. Additionally, we prove a lower bound showing that exploiting the similarity between the policies is not possible in general under linear bandit feedback. Finally, for a full-information variant, we provide a regret bound scaling with the information radius of the policy set.

Best-of-Both-Worlds Algorithms for Linear Contextual Bandits

We study best-of-both-worlds algorithms for $K$-armed linear contextual bandits. Our algorithms deliver near-optimal regret bounds in both the adversarial and stochastic regimes, without prior knowledge about the environment. In the stochastic regime, we achieve the polylogarithmic rate $\frac{(dK)^2\mathrm{poly}\log(dKT)}{\Delta_{\min}}$, where $\Delta_{\min}$ is the minimum suboptimality gap over the $d$-dimensional context space. In the adversarial regime, we obtain either the first-order $\widetilde{O}(dK\sqrt{L^*})$ bound, or the second-order $\widetilde{O}(dK\sqrt{\Lambda^*})$ bound, where $L^*$ is the cumulative loss of the best action and $\Lambda^*$ is a notion of the cumulative second moment for the losses incurred by the algorithm. Moreover, we develop an algorithm based on FTRL with Shannon entropy regularizer that does not require the knowledge of the inverse of the covariance matrix, and achieves a polylogarithmic regret in the stochastic regime while obtaining $\widetilde{O}\big(dK\sqrt{T}\big)$ regret bounds in the adversarial regime.