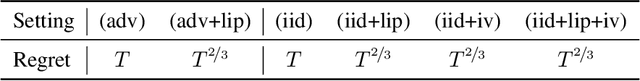
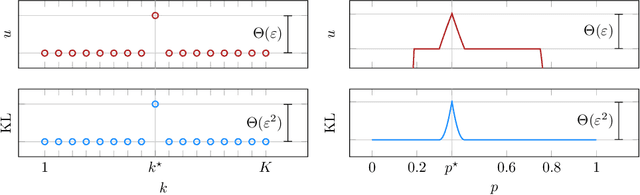
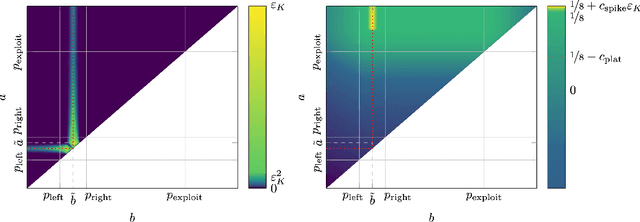
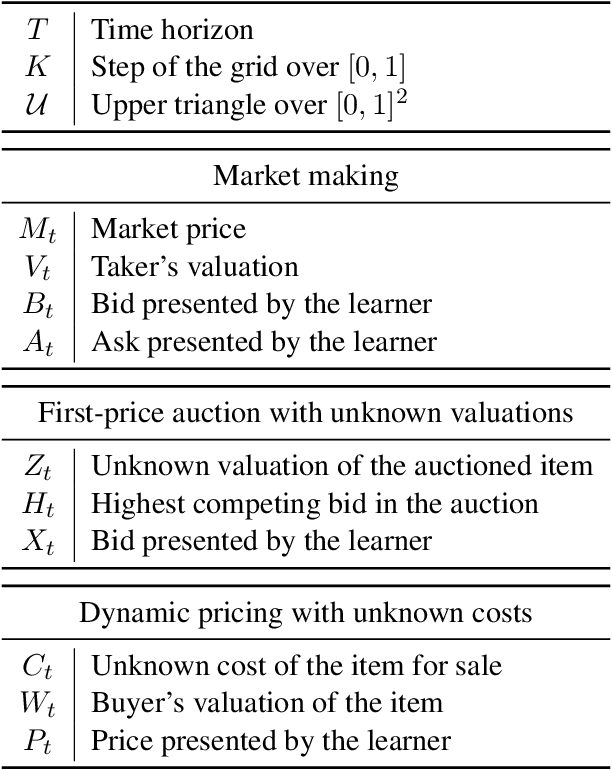
Market Making without Regret

We consider a sequential decision-making setting where, at every round $t$, a market maker posts a bid price $B_t$ and an ask price $A_t$ to an incoming trader (the taker) with a private valuation for one unit of some asset. If the trader's valuation is lower than the bid price, or higher than the ask price, then a trade (sell or buy) occurs. If a trade happens at round $t$, then letting $M_t$ be the market price (observed only at the end of round $t$), the maker's utility is $M_t - B_t$ if the maker bought the asset, and $A_t - M_t$ if they sold it. We characterize the maker's regret with respect to the best fixed choice of bid and ask pairs under a variety of assumptions (adversarial, i.i.d., and their variants) on the sequence of market prices and valuations. Our upper bound analysis unveils an intriguing connection relating market making to first-price auctions and dynamic pricing. Our main technical contribution is a lower bound for the i.i.d. case with Lipschitz distributions and independence between prices and valuations. The difficulty in the analysis stems from the unique structure of the reward and feedback functions, allowing an algorithm to acquire information by graduating the "cost of exploration" in an arbitrary way.

Fair Online Bilateral Trade

In online bilateral trade, a platform posts prices to incoming pairs of buyers and sellers that have private valuations for a certain good. If the price is lower than the buyers' valuation and higher than the sellers' valuation, then a trade takes place. Previous work focused on the platform perspective, with the goal of setting prices maximizing the gain from trade (the sum of sellers' and buyers' utilities). Gain from trade is, however, potentially unfair to traders, as they may receive highly uneven shares of the total utility. In this work we enforce fairness by rewarding the platform with the fair gain from trade, defined as the minimum between sellers' and buyers' utilities. After showing that any no-regret learning algorithm designed to maximize the sum of the utilities may fail badly with fair gain from trade, we present our main contribution: a complete characterization of the regret regimes for fair gain from trade when, after each interaction, the platform only learns whether each trader accepted the current price. Specifically, we prove the following regret bounds: $\Theta(\ln T)$ in the deterministic setting, $\Omega(T)$ in the stochastic setting, and $\tilde{\Theta}(T^{2/3})$ in the stochastic setting when sellers' and buyers' valuations are independent of each other. We conclude by providing tight regret bounds when, after each interaction, the platform is allowed to observe the true traders' valuations.

Trading Volume Maximization with Online Learning

We explore brokerage between traders in an online learning framework. At any round $t$, two traders meet to exchange an asset, provided the exchange is mutually beneficial. The broker proposes a trading price, and each trader tries to sell their asset or buy the asset from the other party, depending on whether the price is higher or lower than their private valuations. A trade happens if one trader is willing to sell and the other is willing to buy at the proposed price. Previous work provided guidance to a broker aiming at enhancing traders' total earnings by maximizing the gain from trade, defined as the sum of the traders' net utilities after each interaction. In contrast, we investigate how the broker should behave to maximize the trading volume, i.e., the total number of trades. We model the traders' valuations as an i.i.d. process with an unknown distribution. If the traders' valuations are revealed after each interaction (full-feedback), and the traders' valuations cumulative distribution function (cdf) is continuous, we provide an algorithm achieving logarithmic regret and show its optimality up to constant factors. If only their willingness to sell or buy at the proposed price is revealed after each interaction ($2$-bit feedback), we provide an algorithm achieving poly-logarithmic regret when the traders' valuations cdf is Lipschitz and show that this rate is near-optimal. We complement our results by analyzing the implications of dropping the regularity assumptions on the unknown traders' valuations cdf. If we drop the continuous cdf assumption, the regret rate degrades to $\Theta(\sqrt{T})$ in the full-feedback case, where $T$ is the time horizon. If we drop the Lipschitz cdf assumption, learning becomes impossible in the $2$-bit feedback case.

An Online Learning Theory of Brokerage

We investigate brokerage between traders from an online learning perspective. At any round $t$, two traders arrive with their private valuations, and the broker proposes a trading price. Unlike other bilateral trade problems already studied in the online learning literature, we focus on the case where there are no designated buyer and seller roles: each trader will attempt to either buy or sell depending on the current price of the good. We assume the agents' valuations are drawn i.i.d. from a fixed but unknown distribution. If the distribution admits a density bounded by some constant $M$, then, for any time horizon $T$: $\bullet$ If the agents' valuations are revealed after each interaction, we provide an algorithm achieving regret $M \log T$ and show this rate is optimal, up to constant factors. $\bullet$ If only their willingness to sell or buy at the proposed price is revealed after each interaction, we provide an algorithm achieving regret $\sqrt{M T}$ and show this rate is optimal, up to constant factors. Finally, if we drop the bounded density assumption, we show that the optimal rate degrades to $\sqrt{T}$ in the first case, and the problem becomes unlearnable in the second.

The Role of Transparency in Repeated First-Price Auctions with Unknown Valuations

We study the problem of regret minimization for a single bidder in a sequence of first-price auctions where the bidder knows the item's value only if the auction is won. Our main contribution is a complete characterization, up to logarithmic factors, of the minimax regret in terms of the auction's transparency, which regulates the amount of information on competing bids disclosed by the auctioneer at the end of each auction. Our results hold under different assumptions (stochastic, adversarial, and their smoothed variants) on the environment generating the bidder's valuations and competing bids. These minimax rates reveal how the interplay between transparency and the nature of the environment affects how fast one can learn to bid optimally in first-price auctions.

On the Minimax Regret for Online Learning with Feedback Graphs

In this work, we improve on the upper and lower bounds for the regret of online learning with strongly observable undirected feedback graphs. The best known upper bound for this problem is $\mathcal{O}\bigl(\sqrt{\alpha T\ln K}\bigr)$, where $K$ is the number of actions, $\alpha$ is the independence number of the graph, and $T$ is the time horizon. The $\sqrt{\ln K}$ factor is known to be necessary when $\alpha = 1$ (the experts case). On the other hand, when $\alpha = K$ (the bandits case), the minimax rate is known to be $\Theta\bigl(\sqrt{KT}\bigr)$, and a lower bound $\Omega\bigl(\sqrt{\alpha T}\bigr)$ is known to hold for any $\alpha$. Our improved upper bound $\mathcal{O}\bigl(\sqrt{\alpha T(1+\ln(K/\alpha))}\bigr)$ holds for any $\alpha$ and matches the lower bounds for bandits and experts, while interpolating intermediate cases. To prove this result, we use FTRL with $q$-Tsallis entropy for a carefully chosen value of $q \in [1/2, 1)$ that varies with $\alpha$. The analysis of this algorithm requires a new bound on the variance term in the regret. We also show how to extend our techniques to time-varying graphs, without requiring prior knowledge of their independence numbers. Our upper bound is complemented by an improved $\Omega\bigl(\sqrt{\alpha T(\ln K)/(\ln\alpha)}\bigr)$ lower bound for all $\alpha > 1$, whose analysis relies on a novel reduction to multitask learning. This shows that a logarithmic factor is necessary as soon as $\alpha < K$.

Repeated Bilateral Trade Against a Smoothed Adversary

We study repeated bilateral trade where an adaptive $\sigma$-smooth adversary generates the valuations of sellers and buyers. We provide a complete characterization of the regret regimes for fixed-price mechanisms under different feedback models in the two cases where the learner can post either the same or different prices to buyers and sellers. We begin by showing that the minimax regret after $T$ rounds is of order $\sqrt{T}$ in the full-feedback scenario. Under partial feedback, any algorithm that has to post the same price to buyers and sellers suffers worst-case linear regret. However, when the learner can post two different prices at each round, we design an algorithm enjoying regret of order $T^{3/4}$ ignoring log factors. We prove that this rate is optimal by presenting a surprising $T^{3/4}$ lower bound, which is the main technical contribution of the paper.

Regret Analysis of Dyadic Search

We analyze the cumulative regret of the Dyadic Search algorithm of Bachoc et al. [2022].

A Near-Optimal Algorithm for Univariate Zeroth-Order Budget Convex Optimization

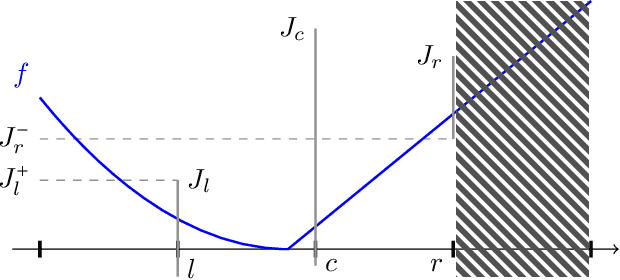
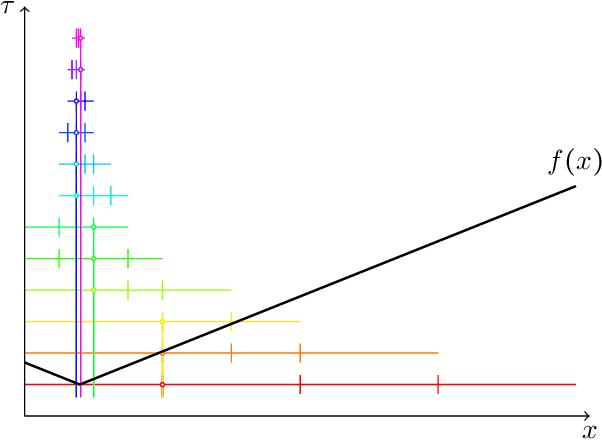
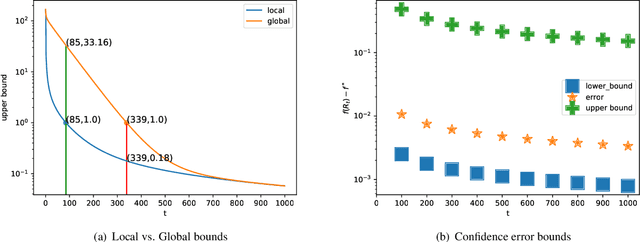
This paper studies a natural generalization of the problem of minimizing a univariate convex function $f$ by querying its values sequentially. At each time-step $t$, the optimizer can invest a budget $b_t$ in a query point $X_t$ of their choice to obtain a fuzzy evaluation of $f$ at $X_t$ whose accuracy depends on the amount of budget invested in $X_t$ across times. This setting is motivated by the minimization of objectives whose values can only be determined approximately through lengthy or expensive computations. We design an any-time parameter-free algorithm called Dyadic Search, for which we prove near-optimal optimization error guarantees. As a byproduct of our analysis, we show that the classical dependence on the global Lipschitz constant in the error bounds is an artifact of the granularity of the budget. Finally, we illustrate our theoretical findings with numerical simulations.

Online Learning in Supply-Chain Games

We study a repeated game between a supplier and a retailer who want to maximize their respective profits without full knowledge of the problem parameters. After characterizing the uniqueness of the Stackelberg equilibrium of the stage game with complete information, we show that even with partial knowledge of the joint distribution of demand and production costs, natural learning dynamics guarantee convergence of the joint strategy profile of supplier and retailer to the Stackelberg equilibrium of the stage game. We also prove finite-time bounds on the supplier's regret and asymptotic bounds on the retailer's regret, where the specific rates depend on the type of knowledge preliminarily available to the players. In the special case when the supplier is not strategic (vertical integration), we prove optimal finite-time regret bounds on the retailer's regret (or, equivalently, the social welfare) when costs and demand are adversarially generated and the demand is censored.