Mostafa Rahmani
Enhancing Open RAN Digital Twin Through Power Consumption Measurement
Jul 01, 2025Abstract:The increasing demand for high-speed, ultra-reliable and low-latency communications in 5G and beyond networks has led to a significant increase in power consumption, particularly within the Radio Access Network (RAN). This growing energy demand raises operational and sustainability challenges for mobile network operators, requiring novel solutions to enhance energy efficiency while maintaining Quality of Service (QoS). 5G networks are evolving towards disaggregated, programmable, and intelligent architectures, with Open Radio Access Network (O-RAN) spearheaded by the O-RAN Alliance, enabling greater flexibility, interoperability, and cost-effectiveness. However, this disaggregated approach introduces new complexities, especially in terms of power consumption across different network components, including Open Radio Units (RUs), Open Distributed Units (DUs) and Open Central Units (CUs). Understanding the power efficiency of different O-RAN functional splits is crucial for optimising energy consumption and network sustainability. In this paper, we present a comprehensive measurement study of power consumption in RUs, DUs and CUs under varying network loads, specifically analysing the impact of Physical resource block (PRB) utilisation in Split 8 and Split 7.2b. The measurements were conducted on both software-defined radio (SDR)-based RUs and commercial indoor and outdoor RU, as well as their corresponding DU and CU. By evaluating real-world hardware deployments under different operational conditions, this study provides empirical insights into the power efficiency of various O-RAN configurations. The results highlight that power consumption does not scale significantly with network load, suggesting that a large portion of energy consumption remains constant regardless of traffic demand.
Pilot and Data Power Control for Uplink Cell-free massive MIMO
Feb 26, 2025Abstract:This paper introduces a novel iterative algorithm for optimizing pilot and data power control (PC) in cell-free massive multiple-input multiple-output (CF-mMIMO) systems, aiming to enhance system performance under real-time channel conditions. The approach begins by deriving the signal-to-interference-plus-noise ratio (SINR) using a matched filtering receiver and formulating a min-max optimization problem to minimize the normalized mean square error (NMSE). Utilizing McCormick relaxation, the algorithm adjusts pilot power dynamically, ensuring efficient channel estimation. A subsequent max-min optimization problem allocates data power, balancing fairness and efficiency. The iterative process refines pilot and data power allocations based on updated channel state information (CSI) and NMSE results, optimizing spectral efficiency. By leveraging geometric programming (GP) for data power allocation, the proposed method achieves a robust trade-off between simplicity and performance, significantly improving system capacity and fairness. The simulation results demonstrate that dynamic adjustment of both pilot and data PC substantially enhances overall spectral efficiency and fairness, outperforming the existing schemes in the literature.
DeBaTeR: Denoising Bipartite Temporal Graph for Recommendation
Nov 14, 2024



Abstract:Due to the difficulty of acquiring large-scale explicit user feedback, implicit feedback (e.g., clicks or other interactions) is widely applied as an alternative source of data, where user-item interactions can be modeled as a bipartite graph. Due to the noisy and biased nature of implicit real-world user-item interactions, identifying and rectifying noisy interactions are vital to enhance model performance and robustness. Previous works on purifying user-item interactions in collaborative filtering mainly focus on mining the correlation between user/item embeddings and noisy interactions, neglecting the benefit of temporal patterns in determining noisy interactions. Time information, while enhancing the model utility, also bears its natural advantage in helping to determine noisy edges, e.g., if someone usually watches horror movies at night and talk shows in the morning, a record of watching a horror movie in the morning is more likely to be noisy interaction. Armed with this observation, we introduce a simple yet effective mechanism for generating time-aware user/item embeddings and propose two strategies for denoising bipartite temporal graph in recommender systems (DeBaTeR): the first is through reweighting the adjacency matrix (DeBaTeR-A), where a reliability score is defined to reweight the edges through both soft assignment and hard assignment; the second is through reweighting the loss function (DeBaTeR-L), where weights are generated to reweight user-item samples in the losses. Extensive experiments have been conducted to demonstrate the efficacy of our methods and illustrate how time information indeed helps identifying noisy edges.
Automated Data Denoising for Recommendation
May 26, 2023Abstract:In real-world scenarios, most platforms collect both large-scale, naturally noisy implicit feedback and small-scale yet highly relevant explicit feedback. Due to the issue of data sparsity, implicit feedback is often the default choice for training recommender systems (RS), however, such data could be very noisy due to the randomness and diversity of user behaviors. For instance, a large portion of clicks may not reflect true user preferences and many purchases may result in negative reviews or returns. Fortunately, by utilizing the strengths of both types of feedback to compensate for the weaknesses of the other, we can mitigate the above issue at almost no cost. In this work, we propose an Automated Data Denoising framework, \textbf{\textit{AutoDenoise}}, for recommendation, which uses a small number of explicit data as validation set to guide the recommender training. Inspired by the generalized definition of curriculum learning (CL), AutoDenoise learns to automatically and dynamically assign the most appropriate (discrete or continuous) weights to each implicit data sample along the training process under the guidance of the validation performance. Specifically, we use a delicately designed controller network to generate the weights, combine the weights with the loss of each input data to train the recommender system, and optimize the controller with reinforcement learning to maximize the expected accuracy of the trained RS on the noise-free validation set. Thorough experiments indicate that AutoDenoise is able to boost the performance of the state-of-the-art recommendation algorithms on several public benchmark datasets.
Robust Projection based Anomaly Extraction (RPE) in Univariate Time-Series
May 31, 2022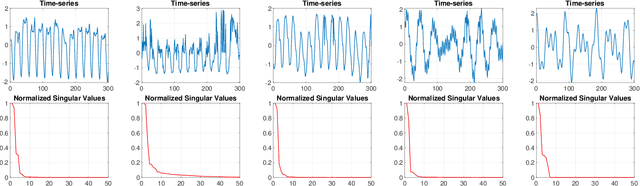

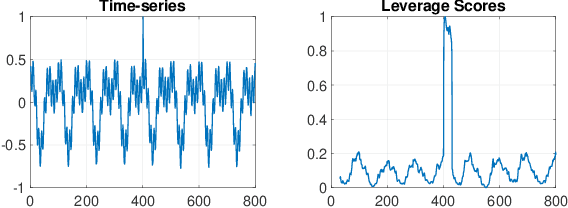

Abstract:This paper presents a novel, closed-form, and data/computation efficient online anomaly detection algorithm for time-series data. The proposed method, dubbed RPE, is a window-based method and in sharp contrast to the existing window-based methods, it is robust to the presence of anomalies in its window and it can distinguish the anomalies in time-stamp level. RPE leverages the linear structure of the trajectory matrix of the time-series and employs a robust projection step which makes the algorithm able to handle the presence of multiple arbitrarily large anomalies in its window. A closed-form/non-iterative algorithm for the robust projection step is provided and it is proved that it can identify the corrupted time-stamps. RPE is a great candidate for the applications where a large training data is not available which is the common scenario in the area of time-series. An extensive set of numerical experiments show that RPE can outperform the existing approaches with a notable margin.
Provable Clustering of a Union of Linear Manifolds Using Optimal Directions
Jan 08, 2022
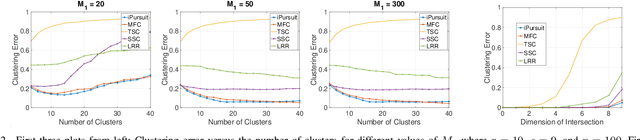
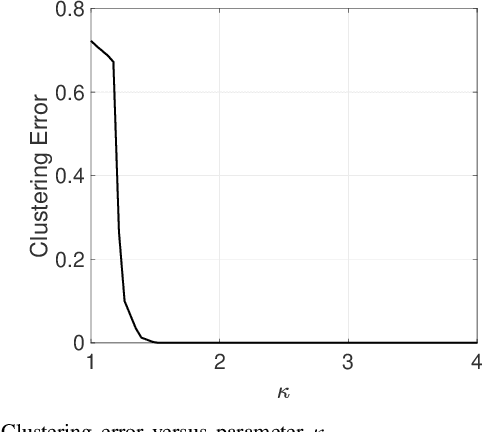
Abstract:This paper focuses on the Matrix Factorization based Clustering (MFC) method which is one of the few closed form algorithms for the subspace clustering problem. Despite being simple, closed-form, and computation-efficient, MFC can outperform the other sophisticated subspace clustering methods in many challenging scenarios. We reveal the connection between MFC and the Innovation Pursuit (iPursuit) algorithm which was shown to be able to outperform the other spectral clustering based methods with a notable margin especially when the span of clusters are close. A novel theoretical study is presented which sheds light on the key performance factors of both algorithms (MFC/iPursuit) and it is shown that both algorithms can be robust to notable intersections between the span of clusters. Importantly, in contrast to the theoretical guarantees of other algorithms which emphasized on the distance between the subspaces as the key performance factor and without making the innovation assumption, it is shown that the performance of MFC/iPursuit mainly depends on the distance between the innovative components of the clusters.
Non-Local Feature Aggregation on Graphs via Latent Fixed Data Structures
Aug 16, 2021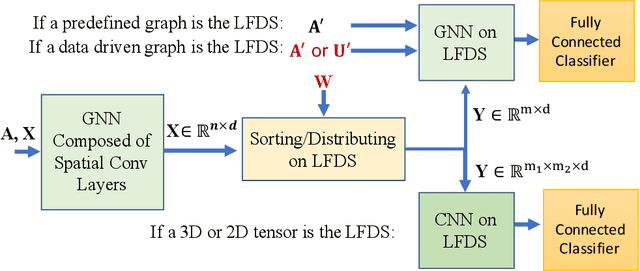
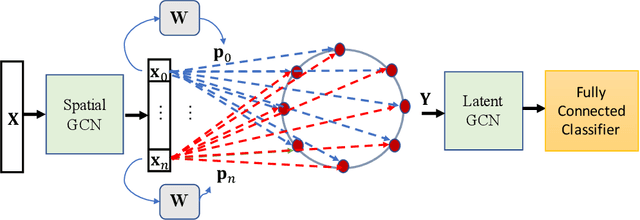
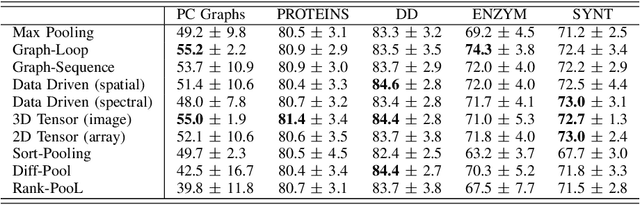
Abstract:In contrast to image/text data whose order can be used to perform non-local feature aggregation in a straightforward way using the pooling layers, graphs lack the tensor representation and mostly the element-wise max/mean function is utilized to aggregate the locally extracted feature vectors. In this paper, we present a novel approach for global feature aggregation in Graph Neural Networks (GNNs) which utilizes a Latent Fixed Data Structure (LFDS) to aggregate the extracted feature vectors. The locally extracted feature vectors are sorted/distributed on the LFDS and a latent neural network (CNN/GNN) is utilized to perform feature aggregation on the LFDS. The proposed approach is used to design several novel global feature aggregation methods based on the choice of the LFDS. We introduce multiple LFDSs including loop, 3D tensor (image), sequence, data driven graphs and an algorithm which sorts/distributes the extracted local feature vectors on the LFDS. While the computational complexity of the proposed methods are linear with the order of input graphs, they achieve competitive or better results.
Provable Data Clustering via Innovation Search
Aug 16, 2021
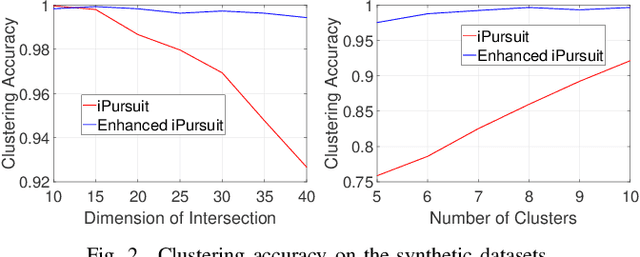

Abstract:This paper studies the subspace clustering problem in which data points collected from high-dimensional ambient space lie in a union of linear subspaces. Subspace clustering becomes challenging when the dimension of intersection between subspaces is large and most of the self-representation based methods are sensitive to the intersection between the span of clusters. In sharp contrast to the self-representation based methods, a recently proposed clustering method termed Innovation Pursuit, computed a set of optimal directions (directions of innovation) to build the adjacency matrix. This paper focuses on the Innovation Pursuit Algorithm to shed light on its impressive performance when the subspaces are heavily intersected. It is shown that in contrast to most of the existing methods which require the subspaces to be sufficiently incoherent with each other, Innovation Pursuit only requires the innovative components of the subspaces to be sufficiently incoherent with each other. These new sufficient conditions allow the clusters to be strongly close to each other. Motivated by the presented theoretical analysis, a simple yet effective projection based technique is proposed which we show with both numerical and theoretical results that it can boost the performance of Innovation Pursuit.
Closed-Form, Provable, and Robust PCA via Leverage Statistics and Innovation Search
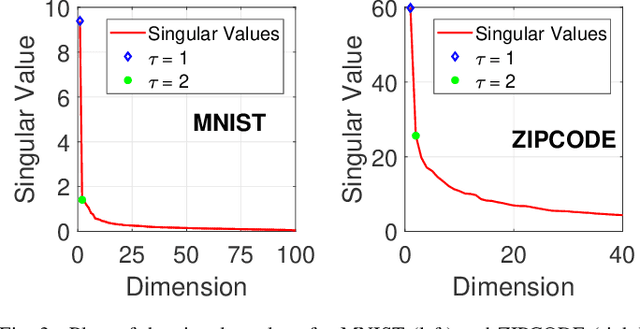
Jun 23, 2021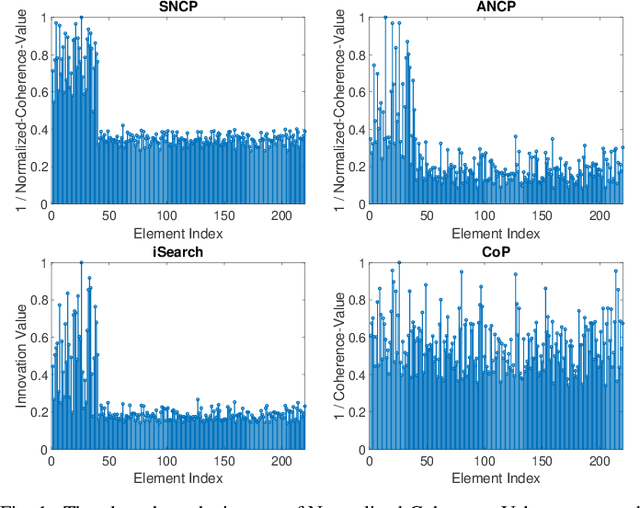
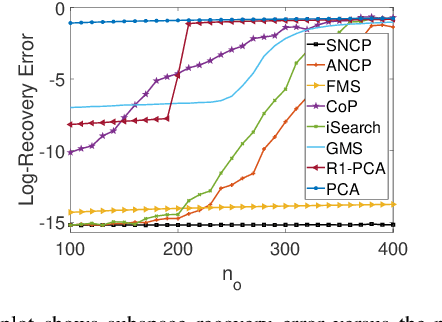
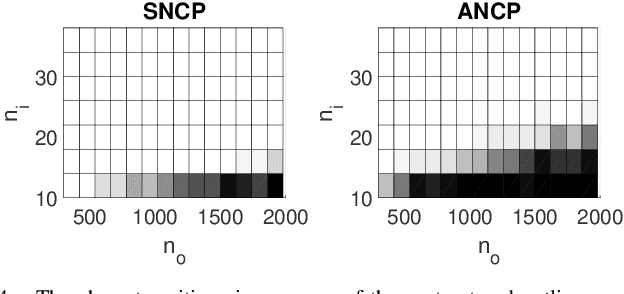
Abstract:The idea of Innovation Search, which was initially proposed for data clustering, was recently used for outlier detection. In the application of Innovation Search for outlier detection, the directions of innovation were utilized to measure the innovation of the data points. We study the Innovation Values computed by the Innovation Search algorithm under a quadratic cost function and it is proved that Innovation Values with the new cost function are equivalent to Leverage Scores. This interesting connection is utilized to establish several theoretical guarantees for a Leverage Score based robust PCA method and to design a new robust PCA method. The theoretical results include performance guarantees with different models for the distribution of outliers and the distribution of inliers. In addition, we demonstrate the robustness of the algorithms against the presence of noise. The numerical and theoretical studies indicate that while the presented approach is fast and closed-form, it can outperform most of the existing algorithms.
Outlier Detection and Data Clustering via Innovation Search
Dec 30, 2019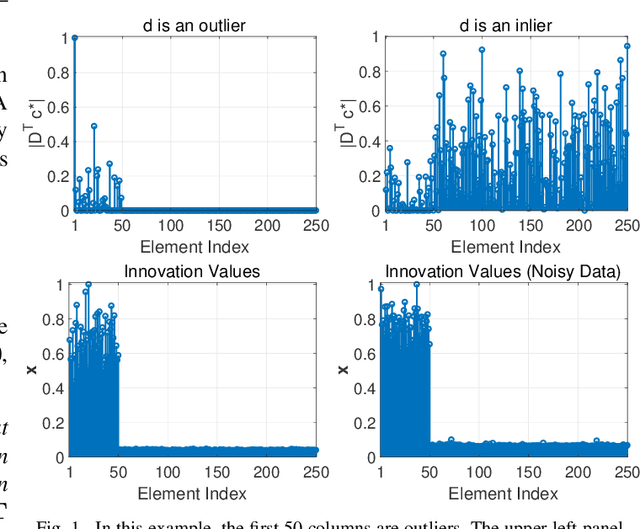
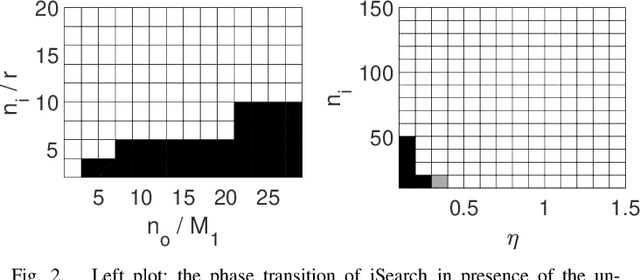
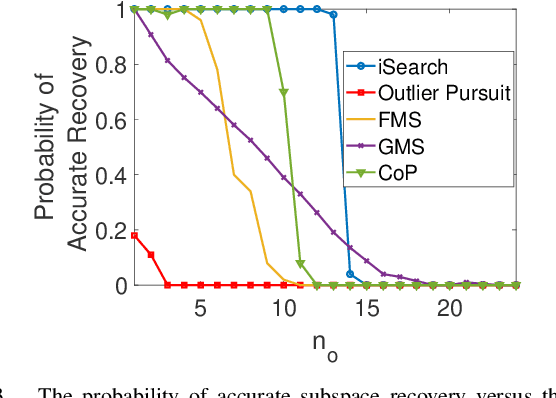
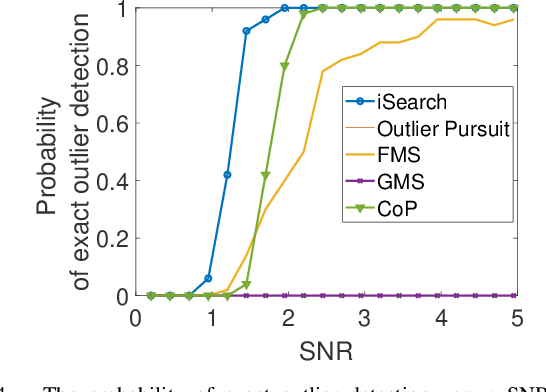
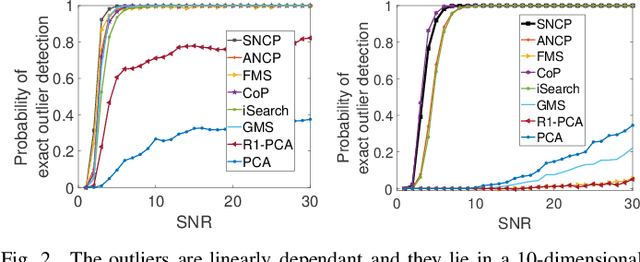
Abstract:The idea of Innovation Search was proposed as a data clustering method in which the directions of innovation were utilized to compute the adjacency matrix and it was shown that Innovation Pursuit can notably outperform the self representation based subspace clustering methods. In this paper, we present a new discovery that the directions of innovation can be used to design a provable and strong robust (to outlier) PCA method. The proposed approach, dubbed iSearch, uses the direction search optimization problem to compute an optimal direction corresponding to each data point. iSearch utilizes the directions of innovation to measure the innovation of the data points and it identifies the outliers as the most innovative data points. Analytical performance guarantees are derived for the proposed robust PCA method under different models for the distribution of the outliers including randomly distributed outliers, clustered outliers, and linearly dependent outliers. In addition, we study the problem of outlier detection in a union of subspaces and it is shown that iSearch provably recovers the span of the inliers when the inliers lie in a union of subspaces. Moreover, we present theoretical studies which show that the proposed measure of innovation remains stable in the presence of noise and the performance of iSearch is robust to noisy data. In the challenging scenarios in which the outliers are close to each other or they are close to the span of the inliers, iSearch is shown to remarkably outperform most of the existing methods. The presented method shows that the directions of innovation are useful representation of the data which can be used to perform both data clustering and outlier detection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge