Depth Separation with Multilayer Mean-Field Networks

Depth separation -- why a deeper network is more powerful than a shallower one -- has been a major problem in deep learning theory. Previous results often focus on representation power. For example, arXiv:1904.06984 constructed a function that is easy to approximate using a 3-layer network but not approximable by any 2-layer network. In this paper, we show that this separation is in fact algorithmic: one can learn the function constructed by arXiv:1904.06984 using an overparameterized network with polynomially many neurons efficiently. Our result relies on a new way of extending the mean-field limit to multilayer networks, and a decomposition of loss that factors out the error introduced by the discretization of infinite-width mean-field networks.

A Policy Gradient Framework for Stochastic Optimal Control Problems with Global Convergence Guarantee

In this work, we consider the stochastic optimal control problem in continuous time and a policy gradient method to solve it. In particular, we study the gradient flow for the control, viewed as a continuous time limit of the policy gradient. We prove the global convergence of the gradient flow and establish a convergence rate under some regularity assumptions. The main novelty in the analysis is the notion of local optimal control function, which is introduced to compare the local optimality of the iterate.

Implicit Regularization Leads to Benign Overfitting for Sparse Linear Regression

In deep learning, often the training process finds an interpolator (a solution with 0 training loss), but the test loss is still low. This phenomenon, known as benign overfitting, is a major mystery that received a lot of recent attention. One common mechanism for benign overfitting is implicit regularization, where the training process leads to additional properties for the interpolator, often characterized by minimizing certain norms. However, even for a simple sparse linear regression problem $y = \beta^{*\top} x +\xi$ with sparse $\beta^*$, neither minimum $\ell_1$ or $\ell_2$ norm interpolator gives the optimal test loss. In this work, we give a different parametrization of the model which leads to a new implicit regularization effect that combines the benefit of $\ell_1$ and $\ell_2$ interpolators. We show that training our new model via gradient descent leads to an interpolator with near-optimal test loss. Our result is based on careful analysis of the training dynamics and provides another example of implicit regularization effect that goes beyond norm minimization.

A Neural Network Warm-Start Approach for the Inverse Acoustic Obstacle Scattering Problem

We consider the inverse acoustic obstacle problem for sound-soft star-shaped obstacles in two dimensions wherein the boundary of the obstacle is determined from measurements of the scattered field at a collection of receivers outside the object. One of the standard approaches for solving this problem is to reformulate it as an optimization problem: finding the boundary of the domain that minimizes the $L^2$ distance between computed values of the scattered field and the given measurement data. The optimization problem is computationally challenging since the local set of convexity shrinks with increasing frequency and results in an increasing number of local minima in the vicinity of the true solution. In many practical experimental settings, low frequency measurements are unavailable due to limitations of the experimental setup or the sensors used for measurement. Thus, obtaining a good initial guess for the optimization problem plays a vital role in this environment. We present a neural network warm-start approach for solving the inverse scattering problem, where an initial guess for the optimization problem is obtained using a trained neural network. We demonstrate the effectiveness of our method with several numerical examples. For high frequency problems, this approach outperforms traditional iterative methods such as Gauss-Newton initialized without any prior (i.e., initialized using a unit circle), or initialized using the solution of a direct method such as the linear sampling method. The algorithm remains robust to noise in the scattered field measurements and also converges to the true solution for limited aperture data. However, the number of training samples required to train the neural network scales exponentially in frequency and the complexity of the obstacles considered. We conclude with a discussion of this phenomenon and potential directions for future research.

Understanding Edge-of-Stability Training Dynamics with a Minimalist Example

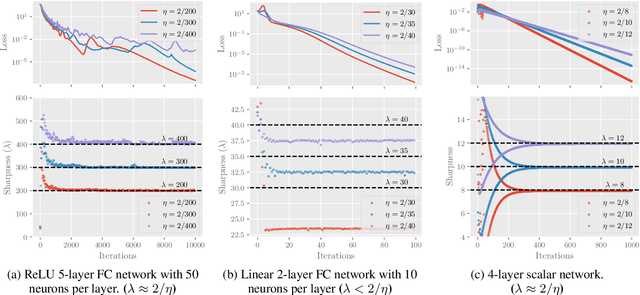
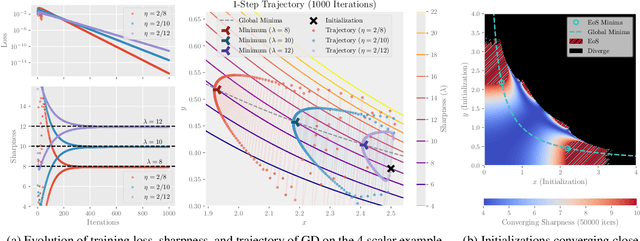
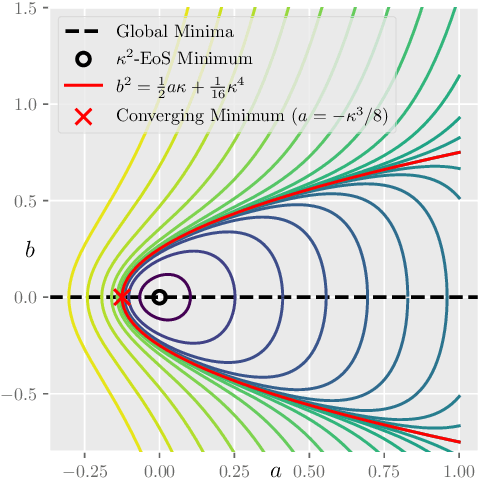
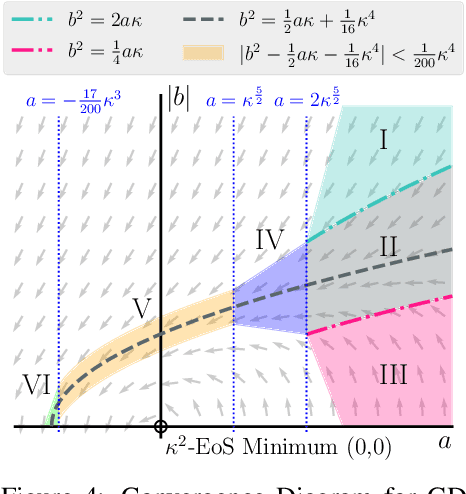
Recently, researchers observed that gradient descent for deep neural networks operates in an ``edge-of-stability'' (EoS) regime: the sharpness (maximum eigenvalue of the Hessian) is often larger than stability threshold 2/$\eta$ (where $\eta$ is the step size). Despite this, the loss oscillates and converges in the long run, and the sharpness at the end is just slightly below $2/\eta$. While many other well-understood nonconvex objectives such as matrix factorization or two-layer networks can also converge despite large sharpness, there is often a larger gap between sharpness of the endpoint and $2/\eta$. In this paper, we study EoS phenomenon by constructing a simple function that has the same behavior. We give rigorous analysis for its training dynamics in a large local region and explain why the final converging point has sharpness close to $2/\eta$. Globally we observe that the training dynamics for our example has an interesting bifurcating behavior, which was also observed in the training of neural nets.

Plateau in Monotonic Linear Interpolation -- A "Biased" View of Loss Landscape for Deep Networks

Monotonic linear interpolation (MLI) - on the line connecting a random initialization with the minimizer it converges to, the loss and accuracy are monotonic - is a phenomenon that is commonly observed in the training of neural networks. Such a phenomenon may seem to suggest that optimization of neural networks is easy. In this paper, we show that the MLI property is not necessarily related to the hardness of optimization problems, and empirical observations on MLI for deep neural networks depend heavily on biases. In particular, we show that interpolating both weights and biases linearly leads to very different influences on the final output, and when different classes have different last-layer biases on a deep network, there will be a long plateau in both the loss and accuracy interpolation (which existing theory of MLI cannot explain). We also show how the last-layer biases for different classes can be different even on a perfectly balanced dataset using a simple model. Empirically we demonstrate that similar intuitions hold on practical networks and realistic datasets.

On Trace of PGD-Like Adversarial Attacks

Adversarial attacks pose safety and security concerns for deep learning applications. Yet largely imperceptible, a strong PGD-like attack may leave strong trace in the adversarial example. Since attack triggers the local linearity of a network, we speculate network behaves in different extents of linearity for benign examples and adversarial examples. Thus, we construct Adversarial Response Characteristics (ARC) features to reflect the model's gradient consistency around the input to indicate the extent of linearity. Under certain conditions, it shows a gradually varying pattern from benign example to adversarial example, as the later leads to Sequel Attack Effect (SAE). ARC feature can be used for informed attack detection (perturbation magnitude is known) with binary classifier, or uninformed attack detection (perturbation magnitude is unknown) with ordinal regression. Due to the uniqueness of SAE to PGD-like attacks, ARC is also capable of inferring other attack details such as loss function, or the ground-truth label as a post-processing defense. Qualitative and quantitative evaluations manifest the effectiveness of ARC feature on CIFAR-10 w/ ResNet-18 and ImageNet w/ ResNet-152 and SwinT-B-IN1K with considerable generalization among PGD-like attacks despite domain shift. Our method is intuitive, light-weighted, non-intrusive, and data-undemanding.

Enhancing Adversarial Robustness for Deep Metric Learning

Owing to security implications of adversarial vulnerability, adversarial robustness of deep metric learning models has to be improved. In order to avoid model collapse due to excessively hard examples, the existing defenses dismiss the min-max adversarial training, but instead learn from a weak adversary inefficiently. Conversely, we propose Hardness Manipulation to efficiently perturb the training triplet till a specified level of hardness for adversarial training, according to a harder benign triplet or a pseudo-hardness function. It is flexible since regular training and min-max adversarial training are its boundary cases. Besides, Gradual Adversary, a family of pseudo-hardness functions is proposed to gradually increase the specified hardness level during training for a better balance between performance and robustness. Additionally, an Intra-Class Structure loss term among benign and adversarial examples further improves model robustness and efficiency. Comprehensive experimental results suggest that the proposed method, although simple in its form, overwhelmingly outperforms the state-of-the-art defenses in terms of robustness, training efficiency, as well as performance on benign examples.

Single Time-scale Actor-critic Method to Solve the Linear Quadratic Regulator with Convergence Guarantees

We propose a single time-scale actor-critic algorithm to solve the linear quadratic regulator (LQR) problem. A least squares temporal difference (LSTD) method is applied to the critic and a natural policy gradient method is used for the actor. We give a proof of convergence with sample complexity $\mO(\ve^{-1} \log(\ve^{-1})^2)$. The method in the proof is applicable to general single time-scale bilevel optimization problem. We also numerically validate our theoretical results on the convergence.

Understanding Deflation Process in Over-parametrized Tensor Decomposition

In this paper we study the training dynamics for gradient flow on over-parametrized tensor decomposition problems. Empirically, such training process often first fits larger components and then discovers smaller components, which is similar to a tensor deflation process that is commonly used in tensor decomposition algorithms. We prove that for orthogonally decomposable tensor, a slightly modified version of gradient flow would follow a tensor deflation process and recover all the tensor components. Our proof suggests that for orthogonal tensors, gradient flow dynamics works similarly as greedy low-rank learning in the matrix setting, which is a first step towards understanding the implicit regularization effect of over-parametrized models for low-rank tensors.