A Neural Network Warm-Start Approach for the Inverse Acoustic Obstacle Scattering Problem

We consider the inverse acoustic obstacle problem for sound-soft star-shaped obstacles in two dimensions wherein the boundary of the obstacle is determined from measurements of the scattered field at a collection of receivers outside the object. One of the standard approaches for solving this problem is to reformulate it as an optimization problem: finding the boundary of the domain that minimizes the $L^2$ distance between computed values of the scattered field and the given measurement data. The optimization problem is computationally challenging since the local set of convexity shrinks with increasing frequency and results in an increasing number of local minima in the vicinity of the true solution. In many practical experimental settings, low frequency measurements are unavailable due to limitations of the experimental setup or the sensors used for measurement. Thus, obtaining a good initial guess for the optimization problem plays a vital role in this environment. We present a neural network warm-start approach for solving the inverse scattering problem, where an initial guess for the optimization problem is obtained using a trained neural network. We demonstrate the effectiveness of our method with several numerical examples. For high frequency problems, this approach outperforms traditional iterative methods such as Gauss-Newton initialized without any prior (i.e., initialized using a unit circle), or initialized using the solution of a direct method such as the linear sampling method. The algorithm remains robust to noise in the scattered field measurements and also converges to the true solution for limited aperture data. However, the number of training samples required to train the neural network scales exponentially in frequency and the complexity of the obstacles considered. We conclude with a discussion of this phenomenon and potential directions for future research.

Efficient Algorithms for t-distributed Stochastic Neighborhood Embedding

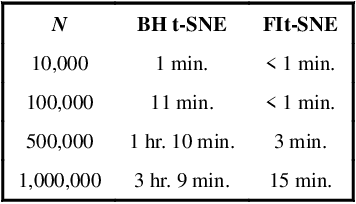
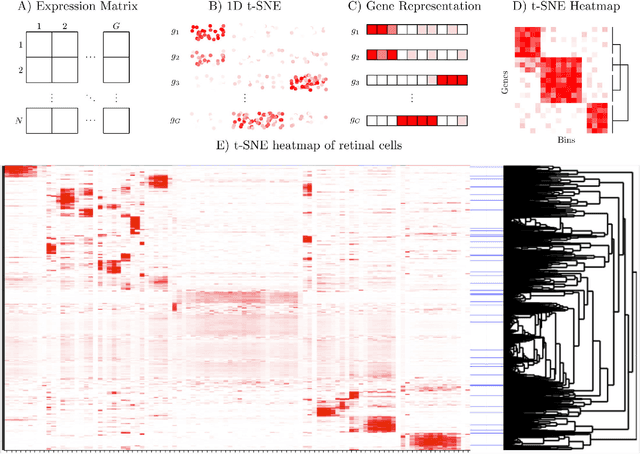
t-distributed Stochastic Neighborhood Embedding (t-SNE) is a method for dimensionality reduction and visualization that has become widely popular in recent years. Efficient implementations of t-SNE are available, but they scale poorly to datasets with hundreds of thousands to millions of high dimensional data-points. We present Fast Fourier Transform-accelerated Interpolation-based t-SNE (FIt-SNE), which dramatically accelerates the computation of t-SNE. The most time-consuming step of t-SNE is a convolution that we accelerate by interpolating onto an equispaced grid and subsequently using the fast Fourier transform to perform the convolution. We also optimize the computation of input similarities in high dimensions using multi-threaded approximate nearest neighbors. We further present a modification to t-SNE called "late exaggeration," which allows for easier identification of clusters in t-SNE embeddings. Finally, for datasets that cannot be loaded into the memory, we present out-of-core randomized principal component analysis (oocPCA), so that the top principal components of a dataset can be computed without ever fully loading the matrix, hence allowing for t-SNE of large datasets to be computed on resource-limited machines.

On the Diffusion Geometry of Graph Laplacians and Applications

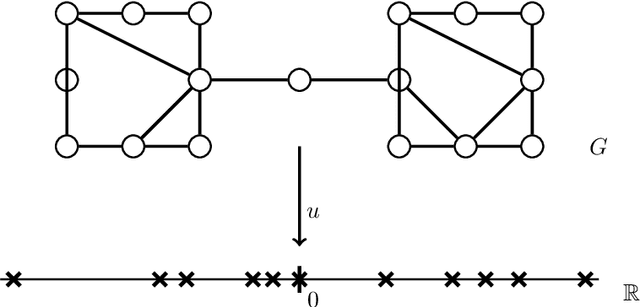
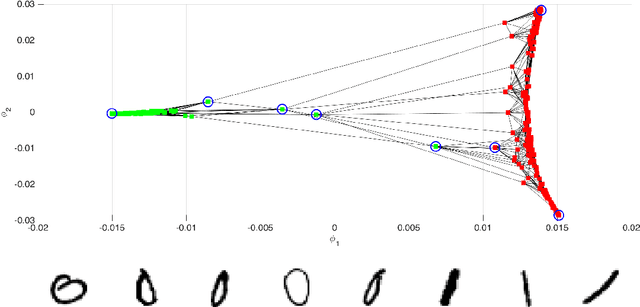
We study directed, weighted graphs $G=(V,E)$ and consider the (not necessarily symmetric) averaging operator $$ (\mathcal{L}u)(i) = -\sum_{j \sim_{} i}{p_{ij} (u(j) - u(i))},$$ where $p_{ij}$ are normalized edge weights. Given a vertex $i \in V$, we define the diffusion distance to a set $B \subset V$ as the smallest number of steps $d_{B}(i) \in \mathbb{N}$ required for half of all random walks started in $i$ and moving randomly with respect to the weights $p_{ij}$ to visit $B$ within $d_{B}(i)$ steps. Our main result is that the eigenfunctions interact nicely with this notion of distance. In particular, if $u$ satisfies $\mathcal{L}u = \lambda u$ on $V$ and $$ B = \left\{ i \in V: - \varepsilon \leq u(i) \leq \varepsilon \right\} \neq \emptyset,$$ then, for all $i \in V$, $$ d_{B}(i) \log{\left( \frac{1}{|1-\lambda|} \right) } \geq \log{\left( \frac{ |u(i)| }{\|u\|_{L^{\infty}}} \right)} - \log{\left(\frac{1}{2} + \varepsilon\right)}.$$ $d_B(i)$ is a remarkably good approximation of $|u|$ in the sense of having very high correlation. The result implies that the classical one-dimensional spectral embedding preserves particular aspects of geometry in the presence of clustered data. We also give a continuous variant of the result which has a connection to the hot spots conjecture.