Out-of-Sample Embedding with Proximity Data: Projection versus Restricted Reconstruction

The problem of using proximity (similarity or dissimilarity) data for the purpose of "adding a point to a vector diagram" was first studied by J.C. Gower in 1968. Since then, a number of methods -- mostly kernel methods -- have been proposed for solving what has come to be called the problem of *out-of-sample embedding*. We survey the various kernel methods that we have encountered and show that each can be derived from one or the other of two competing strategies: *projection* or *restricted reconstruction*. Projection can be analogized to a well-known formula for adding a point to a principal component analysis. Restricted reconstruction poses a different challenge: how to best approximate redoing the entire multivariate analysis while holding fixed the vector diagram that was previously obtained. This strategy results in a nonlinear optimization problem that can be simplified to a unidimensional search. Various circumstances may warrant either projection or restricted reconstruction.

Consistent estimation of generative model representations in the data kernel perspective space

Generative models, such as large language models and text-to-image diffusion models, produce relevant information when presented a query. Different models may produce different information when presented the same query. As the landscape of generative models evolves, it is important to develop techniques to study and analyze differences in model behaviour. In this paper we present novel theoretical results for embedding-based representations of generative models in the context of a set of queries. We establish sufficient conditions for the consistent estimation of the model embeddings in situations where the query set and the number of models grow.

Continuous Multidimensional Scaling

Multidimensional scaling (MDS) is the act of embedding proximity information about a set of $n$ objects in $d$-dimensional Euclidean space. As originally conceived by the psychometric community, MDS was concerned with embedding a fixed set of proximities associated with a fixed set of objects. Modern concerns, e.g., that arise in developing asymptotic theories for statistical inference on random graphs, more typically involve studying the limiting behavior of a sequence of proximities associated with an increasing set of objects. Standard results from the theory of point-to-set maps imply that, if $n$ is fixed and a sequence of proximities converges, then the limit of the embedded structures is the embedded structure of the limiting proximities. But what if $n$ increases? It then becomes necessary to reformulate MDS so that the entire sequence of embedding problems can be viewed as a sequence of optimization problems in a fixed space. We present such a reformulation and derive some consequences.

Semisupervised regression in latent structure networks on unknown manifolds

Random graphs are increasingly becoming objects of interest for modeling networks in a wide range of applications. Latent position random graph models posit that each node is associated with a latent position vector, and that these vectors follow some geometric structure in the latent space. In this paper, we consider random dot product graphs, in which an edge is formed between two nodes with probability given by the inner product of their respective latent positions. We assume that the latent position vectors lie on an unknown one-dimensional curve and are coupled with a response covariate via a regression model. Using the geometry of the underlying latent position vectors, we propose a manifold learning and graph embedding technique to predict the response variable on out-of-sample nodes, and we establish convergence guarantees for these responses. Our theoretical results are supported by simulations and an application to Drosophila brain data.

Popularity Adjusted Block Models are Generalized Random Dot Product Graphs

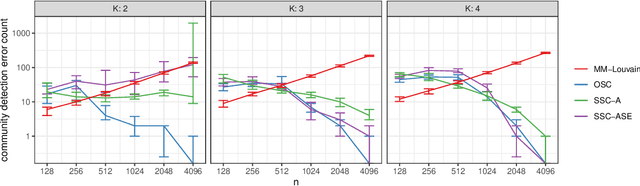
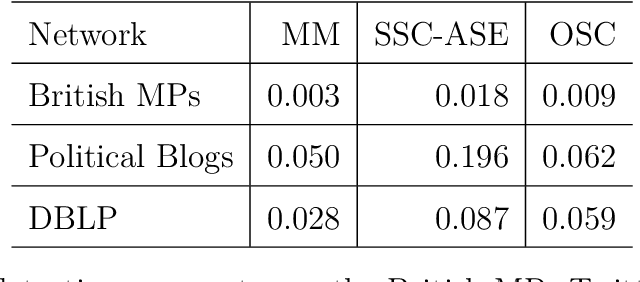
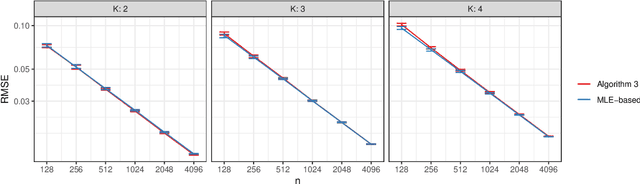
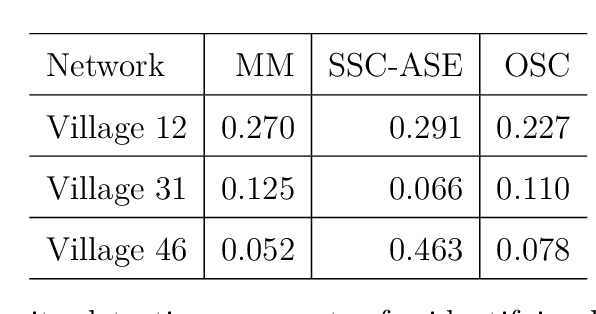
We connect two random graph models, the Popularity Adjusted Block Model (PABM) and the Generalized Random Dot Product Graph (GRDPG), by demonstrating that the PABM is a special case of the GRDPG in which communities correspond to mutually orthogonal subspaces of latent vectors. This insight allows us to construct new algorithms for community detection and parameter estimation for the PABM, as well as improve an existing algorithm that relies on Sparse Subspace Clustering. Using established asymptotic properties of Adjacency Spectral Embedding for the GRDPG, we derive asymptotic properties of these algorithms. In particular, we demonstrate that the absolute number of community detection errors tends to zero as the number of graph vertices tends to infinity. Simulation experiments illustrate these properties.

Rehabilitating Isomap: Euclidean Representation of Geodesic Structure

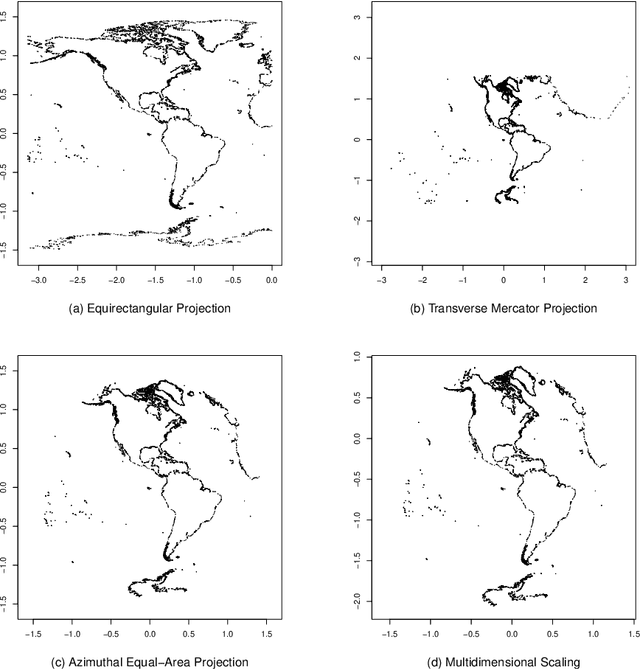
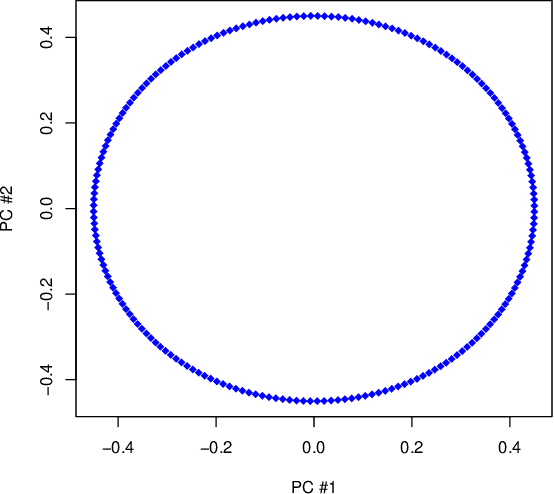
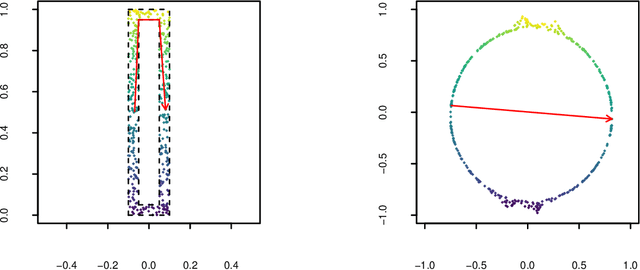
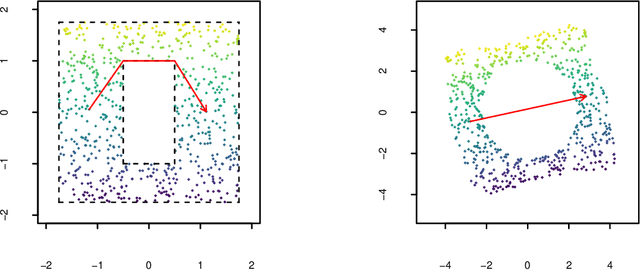
Manifold learning techniques for nonlinear dimension reduction assume that high-dimensional feature vectors lie on a low-dimensional manifold, then attempt to exploit manifold structure to obtain useful low-dimensional Euclidean representations of the data. Isomap, a seminal manifold learning technique, is an elegant synthesis of two simple ideas: the approximation of Riemannian distances with shortest path distances on a graph that localizes manifold structure, and the approximation of shortest path distances with Euclidean distances by multidimensional scaling. We revisit the rationale for Isomap, clarifying what Isomap does and what it does not. In particular, we explore the widespread perception that Isomap should only be used when the manifold is parametrized by a convex region of Euclidean space. We argue that this perception is based on an extremely narrow interpretation of manifold learning as parametrization recovery, and we submit that Isomap is better understood as constructing Euclidean representations of geodesic structure. We reconsider a well-known example that was previously interpreted as evidence of Isomap's limitations, and we re-examine the original analysis of Isomap's convergence properties, concluding that convexity is not required for shortest path distances to converge to Riemannian distances.

Learning 1-Dimensional Submanifolds for Subsequent Inference on Random Dot Product Graphs

A random dot product graph (RDPG) is a generative model for networks in which vertices correspond to positions in a latent Euclidean space and edge probabilities are determined by the dot products of the latent positions. We consider RDPGs for which the latent positions are randomly sampled from an unknown $1$-dimensional submanifold of the latent space. In principle, restricted inference, i.e., procedures that exploit the structure of the submanifold, should be more effective than unrestricted inference; however, it is not clear how to conduct restricted inference when the submanifold is unknown. We submit that techniques for manifold learning can be used to learn the unknown submanifold well enough to realize benefit from restricted inference. To illustrate, we test a hypothesis about the Fr\'{e}chet mean of a small community of vertices, using the complete set of vertices to infer latent structure. We propose test statistics that deploy the Isomap procedure for manifold learning, using shortest path distances on neighborhood graphs constructed from estimated latent positions to estimate arc lengths on the unknown $1$-dimensional submanifold. Unlike conventional applications of Isomap, the estimated latent positions do not lie on the submanifold of interest. We extend existing convergence results for Isomap to this setting and use them to demonstrate that, as the number of auxiliary vertices increases, the power of our test converges to the power of the corresponding test when the submanifold is known.

Fast Embedding for JOFC Using the Raw Stress Criterion

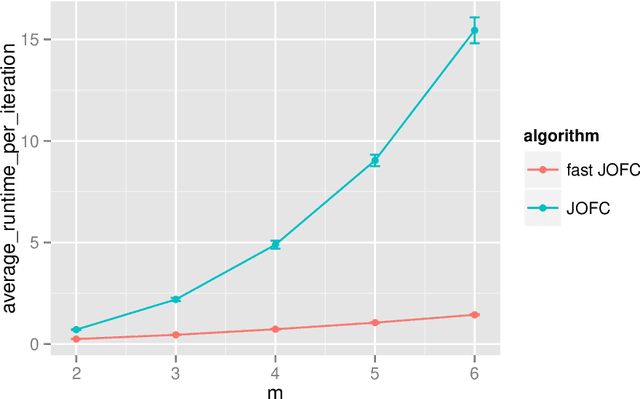
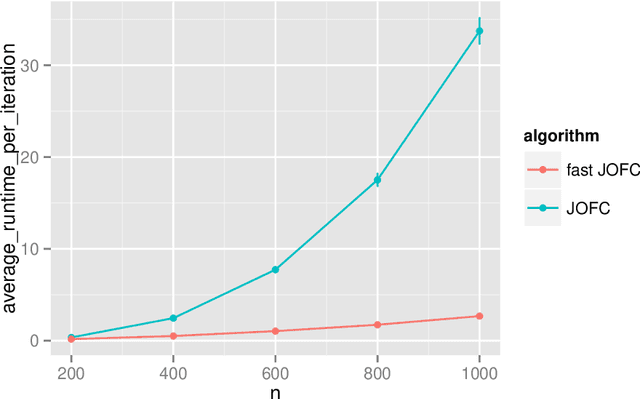
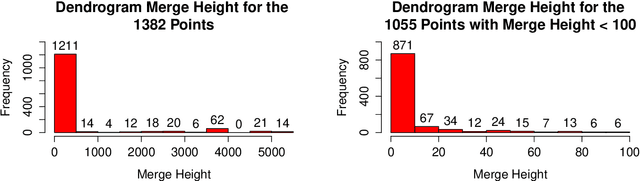
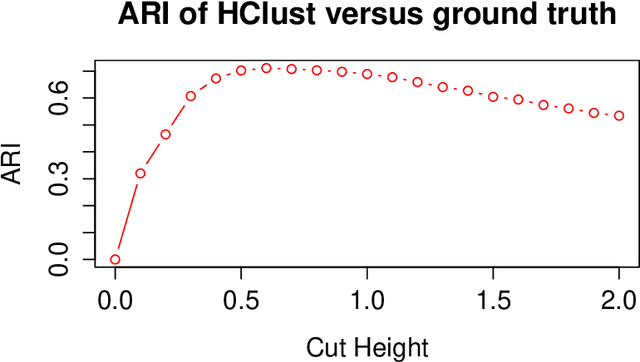
The Joint Optimization of Fidelity and Commensurability (JOFC) manifold matching methodology embeds an omnibus dissimilarity matrix consisting of multiple dissimilarities on the same set of objects. One approach to this embedding optimizes the preservation of fidelity to each individual dissimilarity matrix together with commensurability of each given observation across modalities via iterative majorization of a raw stress error criterion by successive Guttman transforms. In this paper, we exploit the special structure inherent to JOFC to exactly and efficiently compute the successive Guttman transforms, and as a result we are able to greatly speed up the JOFC procedure for both in-sample and out-of-sample embedding. We demonstrate the scalability of our implementation on both real and simulated data examples.

Nonparametric semi-supervised learning of class proportions

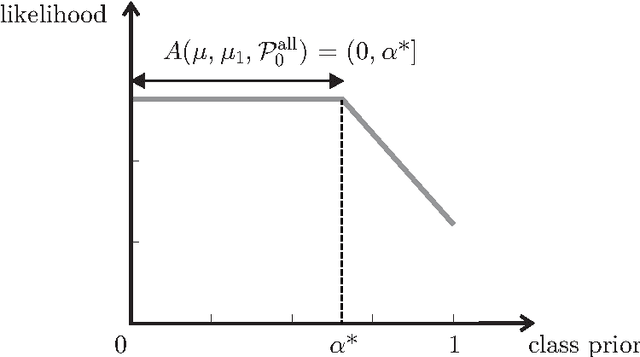
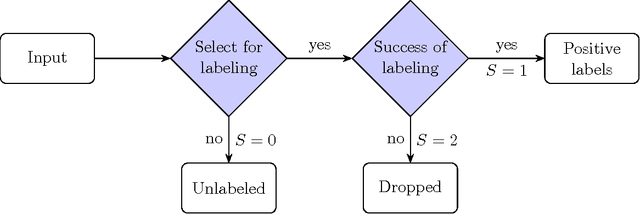
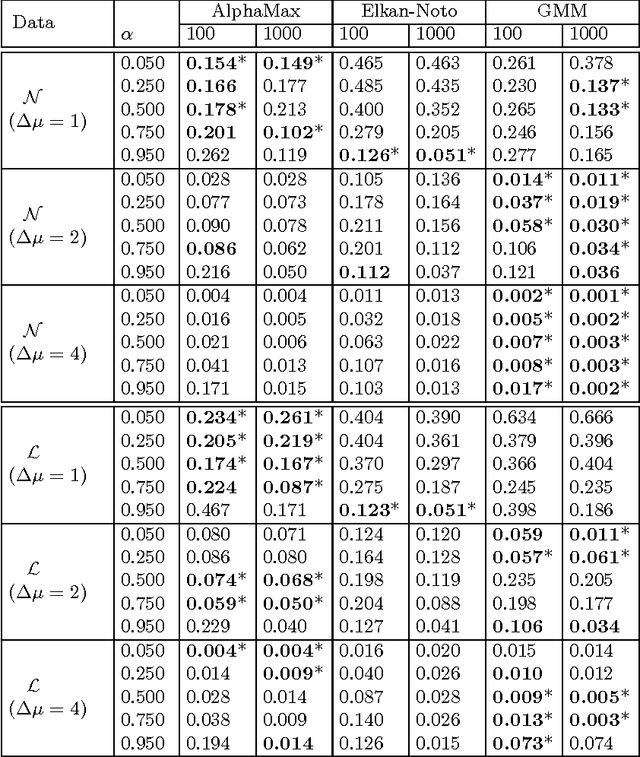
The problem of developing binary classifiers from positive and unlabeled data is often encountered in machine learning. A common requirement in this setting is to approximate posterior probabilities of positive and negative classes for a previously unseen data point. This problem can be decomposed into two steps: (i) the development of accurate predictors that discriminate between positive and unlabeled data, and (ii) the accurate estimation of the prior probabilities of positive and negative examples. In this work we primarily focus on the latter subproblem. We study nonparametric class prior estimation and formulate this problem as an estimation of mixing proportions in two-component mixture models, given a sample from one of the components and another sample from the mixture itself. We show that estimation of mixing proportions is generally ill-defined and propose a canonical form to obtain identifiability while maintaining the flexibility to model any distribution. We use insights from this theory to elucidate the optimization surface of the class priors and propose an algorithm for estimating them. To address the problems of high-dimensional density estimation, we provide practical transformations to low-dimensional spaces that preserve class priors. Finally, we demonstrate the efficacy of our method on univariate and multivariate data.