A Convex Relaxation Approach to Generalization Analysis for Parallel Positively Homogeneous Networks

We propose a general framework for deriving generalization bounds for parallel positively homogeneous neural networks--a class of neural networks whose input-output map decomposes as the sum of positively homogeneous maps. Examples of such networks include matrix factorization and sensing, single-layer multi-head attention mechanisms, tensor factorization, deep linear and ReLU networks, and more. Our general framework is based on linking the non-convex empirical risk minimization (ERM) problem to a closely related convex optimization problem over prediction functions, which provides a global, achievable lower-bound to the ERM problem. We exploit this convex lower-bound to perform generalization analysis in the convex space while controlling the discrepancy between the convex model and its non-convex counterpart. We apply our general framework to a wide variety of models ranging from low-rank matrix sensing, to structured matrix sensing, two-layer linear networks, two-layer ReLU networks, and single-layer multi-head attention mechanisms, achieving generalization bounds with a sample complexity that scales almost linearly with the network width.

ICL-TSVD: Bridging Theory and Practice in Continual Learning with Pre-trained Models

The goal of continual learning (CL) is to train a model that can solve multiple tasks presented sequentially. Recent CL approaches have achieved strong performance by leveraging large pre-trained models that generalize well to downstream tasks. However, such methods lack theoretical guarantees, making them prone to unexpected failures. Conversely, principled CL approaches often fail to achieve competitive performance. In this work, we bridge this gap between theory and practice by integrating an empirically strong approach (RanPAC) into a principled framework, Ideal Continual Learner (ICL), designed to prevent forgetting. Specifically, we lift pre-trained features into a higher dimensional space and formulate an over-parametrized minimum-norm least-squares problem. We find that the lifted features are highly ill-conditioned, potentially leading to large training errors (numerical instability) and increased generalization errors (double descent). We address these challenges by continually truncating the singular value decomposition (SVD) of the lifted features. Our approach, termed ICL-TSVD, is stable with respect to the choice of hyperparameters, can handle hundreds of tasks, and outperforms state-of-the-art CL methods on multiple datasets. Importantly, our method satisfies a recurrence relation throughout its continual learning process, which allows us to prove it maintains small training and generalization errors by appropriately truncating a fraction of SVD factors. This results in a stable continual learning method with strong empirical performance and theoretical guarantees.

Semisupervised regression in latent structure networks on unknown manifolds

Random graphs are increasingly becoming objects of interest for modeling networks in a wide range of applications. Latent position random graph models posit that each node is associated with a latent position vector, and that these vectors follow some geometric structure in the latent space. In this paper, we consider random dot product graphs, in which an edge is formed between two nodes with probability given by the inner product of their respective latent positions. We assume that the latent position vectors lie on an unknown one-dimensional curve and are coupled with a response covariate via a regression model. Using the geometry of the underlying latent position vectors, we propose a manifold learning and graph embedding technique to predict the response variable on out-of-sample nodes, and we establish convergence guarantees for these responses. Our theoretical results are supported by simulations and an application to Drosophila brain data.

Estimating Higher-Order Mixed Memberships via the $\ell_{2,\infty}$ Tensor Perturbation Bound

Higher-order multiway data is ubiquitous in machine learning and statistics and often exhibits community-like structures, where each component (node) along each different mode has a community membership associated with it. In this paper we propose the tensor mixed-membership blockmodel, a generalization of the tensor blockmodel positing that memberships need not be discrete, but instead are convex combinations of latent communities. We establish the identifiability of our model and propose a computationally efficient estimation procedure based on the higher-order orthogonal iteration algorithm (HOOI) for tensor SVD composed with a simplex corner-finding algorithm. We then demonstrate the consistency of our estimation procedure by providing a per-node error bound, which showcases the effect of higher-order structures on estimation accuracy. To prove our consistency result, we develop the $\ell_{2,\infty}$ tensor perturbation bound for HOOI under independent, possibly heteroskedastic, subgaussian noise that may be of independent interest. Our analysis uses a novel leave-one-out construction for the iterates, and our bounds depend only on spectral properties of the underlying low-rank tensor under nearly optimal signal-to-noise ratio conditions such that tensor SVD is computationally feasible. Whereas other leave-one-out analyses typically focus on sequences constructed by analyzing the output of a given algorithm with a small part of the noise removed, our leave-one-out analysis constructions use both the previous iterates and the additional tensor structure to eliminate a potential additional source of error. Finally, we apply our methodology to real and simulated data, including applications to two flight datasets and a trade network dataset, demonstrating some effects not identifiable from the model with discrete community memberships.

Entrywise Recovery Guarantees for Sparse PCA via Sparsistent Algorithms

Sparse Principal Component Analysis (PCA) is a prevalent tool across a plethora of subfields of applied statistics. While several results have characterized the recovery error of the principal eigenvectors, these are typically in spectral or Frobenius norms. In this paper, we provide entrywise $\ell_{2,\infty}$ bounds for Sparse PCA under a general high-dimensional subgaussian design. In particular, our results hold for any algorithm that selects the correct support with high probability, those that are sparsistent. Our bound improves upon known results by providing a finer characterization of the estimation error, and our proof uses techniques recently developed for entrywise subspace perturbation theory.

On Two Distinct Sources of Nonidentifiability in Latent Position Random Graph Models

Two separate and distinct sources of nonidentifiability arise naturally in the context of latent position random graph models, though neither are unique to this setting. In this paper we define and examine these two nonidentifiabilities, dubbed subspace nonidentifiability and model-based nonidentifiability, in the context of random graph inference. We give examples where each type of nonidentifiability comes into play, and we show how in certain settings one need worry about one or the other type of nonidentifiability. Then, we characterize the limit for model-based nonidentifiability both with and without subspace nonidentifiability. We further obtain additional limiting results for covariances and $U$-statistics of stochastic block models and generalized random dot product graphs.

Vertex Nomination, Consistent Estimation, and Adversarial Modification

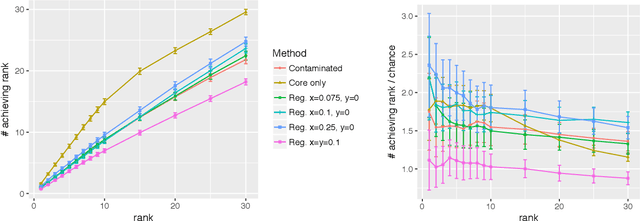
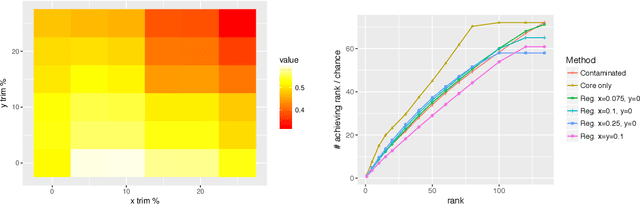
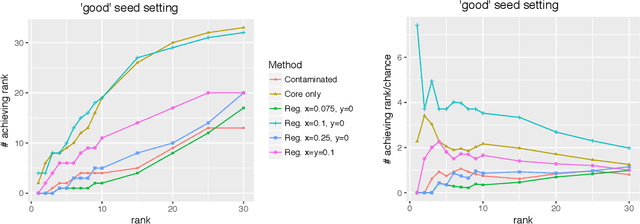
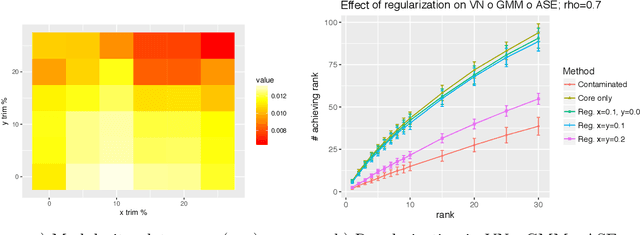
Given a pair of graphs $G_1$ and $G_2$ and a vertex set of interest in $G_1$, the vertex nomination problem seeks to find the corresponding vertices of interest in $G_2$ (if they exist) and produce a rank list of the vertices in $G_2$, with the corresponding vertices of interest in $G_2$ concentrating, ideally, at the top of the rank list. In this paper we study the effect of an adversarial contamination model on the performance of a spectral graph embedding-based vertex nomination scheme. In both real and simulated examples, we demonstrate that this vertex nomination scheme performs effectively in the uncontaminated setting; adversarial network contamination adversely impacts the performance of our VN scheme; and network regularization successfully mitigates the impact of the contamination. In addition to furthering the theoretic basis of consistency in vertex nomination, the adversarial noise model posited herein is grounded in theoretical developments that allow us to frame the role of an adversary in terms of maximal vertex nomination consistency classes.