Enhancing Diffusion-Weighted Images (DWI) for Diffusion MRI: Is it Enough without Non-Diffusion-Weighted B=0 Reference?

Diffusion MRI (dMRI) is essential for studying brain microstructure, but high-resolution imaging remains challenging due to the inherent trade-offs between acquisition time and signal-to-noise ratio (SNR). Conventional methods often optimize only the diffusion-weighted images (DWIs) without considering their relationship with the non-diffusion-weighted (b=0) reference images. However, calculating diffusion metrics, such as the apparent diffusion coefficient (ADC) and diffusion tensor with its derived metrics like fractional anisotropy (FA) and mean diffusivity (MD), relies on the ratio between each DWI and the b=0 image, which is crucial for clinical observation and diagnostics. In this study, we demonstrate that solely enhancing DWIs using a conventional pixel-wise mean squared error (MSE) loss is insufficient, as the error in ratio between generated DWIs and b=0 diverges. We propose a novel ratio loss, defined as the MSE loss between the predicted and ground-truth log of DWI/b=0 ratios. Our results show that incorporating the ratio loss significantly improves the convergence of this ratio error, achieving lower ratio MSE and slightly enhancing the peak signal-to-noise ratio (PSNR) of generated DWIs. This leads to improved dMRI super-resolution and better preservation of b=0 ratio-based features for the derivation of diffusion metrics.

ACE-Net: AutofoCus-Enhanced Convolutional Network for Field Imperfection Estimation with application to high b-value spiral Diffusion MRI

Spatiotemporal magnetic field variations from B0-inhomogeneity and diffusion-encoding-induced eddy-currents can be detrimental to rapid image-encoding schemes such as spiral, EPI and 3D-cones, resulting in undesirable image artifacts. In this work, a data driven approach for automatic estimation of these field imperfections is developed by combining autofocus metrics with deep learning, and by leveraging a compact basis representation of the expected field imperfections. The method was applied to single-shot spiral diffusion MRI at high b-values where accurate estimation of B0 and eddy were obtained, resulting in high quality image reconstruction without need for additional external calibrations.

NLCG-Net: A Model-Based Zero-Shot Learning Framework for Undersampled Quantitative MRI Reconstruction

Typical quantitative MRI (qMRI) methods estimate parameter maps after image reconstructing, which is prone to biases and error propagation. We propose a Nonlinear Conjugate Gradient (NLCG) optimizer for model-based T2/T1 estimation, which incorporates U-Net regularization trained in a scan-specific manner. This end-to-end method directly estimates qMRI maps from undersampled k-space data using mono-exponential signal modeling with zero-shot scan-specific neural network regularization to enable high fidelity T1 and T2 mapping. T2 and T1 mapping results demonstrate the ability of the proposed NLCG-Net to improve estimation quality compared to subspace reconstruction at high accelerations.

Sequence adaptive field-imperfection estimation (SAFE): retrospective estimation and correction of $B_1^+$ and $B_0$ inhomogeneities for enhanced MRF quantification

$B_1^+$ and $B_0$ field-inhomogeneities can significantly reduce accuracy and robustness of MRF's quantitative parameter estimates. Additional $B_1^+$ and $B_0$ calibration scans can mitigate this but add scan time and cannot be applied retrospectively to previously collected data. Here, we proposed a calibration-free sequence-adaptive deep-learning framework, to estimate and correct for $B_1^+$ and $B_0$ effects of any MRF sequence. We demonstrate its capability on arbitrary MRF sequences at 3T, where no training data were previously obtained. Such approach can be applied to any previously-acquired and future MRF-scans. The flexibility in directly applying this framework to other quantitative sequences is also highlighted.

Accurate parameter estimation using scan-specific unsupervised deep learning for relaxometry and MR fingerprinting

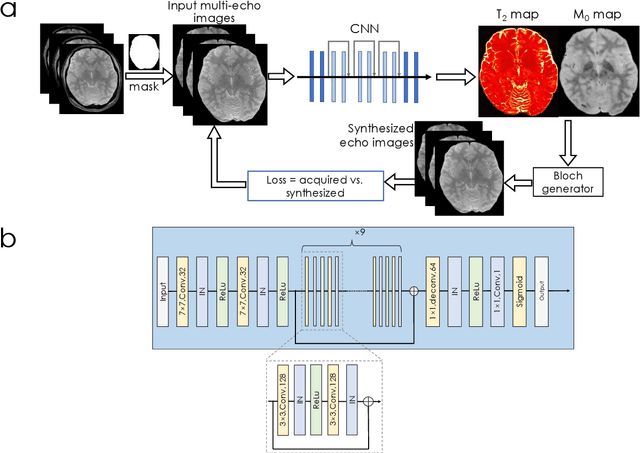
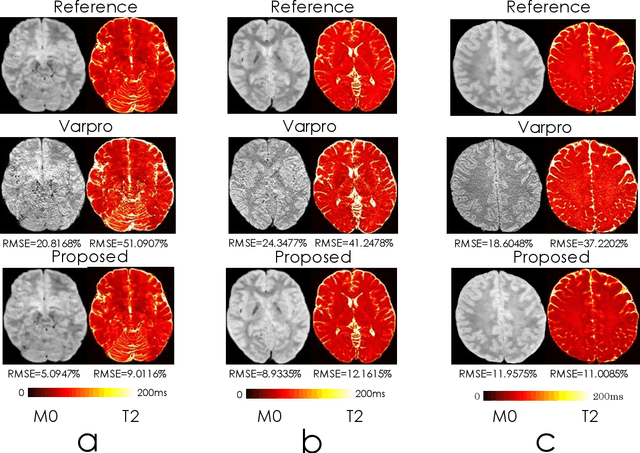
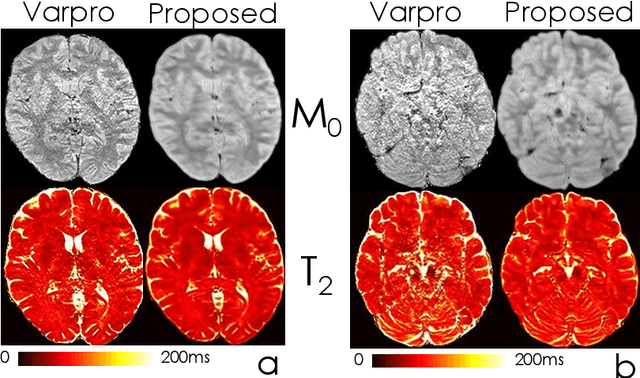
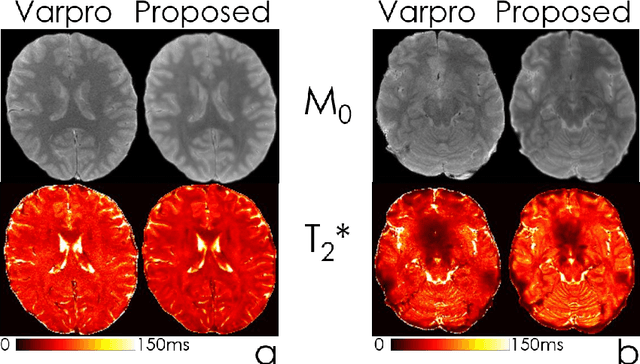
We propose an unsupervised convolutional neural network (CNN) for relaxation parameter estimation. This network incorporates signal relaxation and Bloch simulations while taking advantage of residual learning and spatial relations across neighboring voxels. Quantification accuracy and robustness to noise is shown to be significantly improved compared to standard parameter estimation methods in numerical simulations and in vivo data for multi-echo T2 and T2* mapping. The combination of the proposed network with subspace modeling and MR fingerprinting (MRF) from highly undersampled data permits high quality T1 and T2 mapping.