RiemannLoRA: A Unified Riemannian Framework for Ambiguity-Free LoRA Optimization

Low-Rank Adaptation (LoRA) has become a widely adopted standard for parameter-efficient fine-tuning of large language models (LLMs), significantly reducing memory and computational demands. However, challenges remain, including finding optimal initialization strategies or mitigating overparametrization in low-rank matrix factorization. In this work, we propose a novel approach that addresses both of the challenges simultaneously within a unified framework. Our method treats a set of fixed-rank LoRA matrices as a smooth manifold. Considering adapters as elements on this manifold removes overparametrization, while determining the direction of the fastest loss decrease along the manifold provides initialization. Special care is taken to obtain numerically stable and computationally efficient implementation of our method, using best practices from numerical linear algebra and Riemannian optimization. Experimental results on LLM and diffusion model architectures demonstrate that RiemannLoRA consistently improves both convergence speed and final performance over standard LoRA and its state-of-the-art modifications.

COALA: Numerically Stable and Efficient Framework for Context-Aware Low-Rank Approximation

Recent studies suggest that context-aware low-rank approximation is a useful tool for compression and fine-tuning of modern large-scale neural networks. In this type of approximation, a norm is weighted by a matrix of input activations, significantly improving metrics over the unweighted case. Nevertheless, existing methods for neural networks suffer from numerical instabilities due to their reliance on classical formulas involving explicit Gram matrix computation and their subsequent inversion. We demonstrate that this can degrade the approximation quality or cause numerically singular matrices. To address these limitations, we propose a novel inversion-free regularized framework that is based entirely on stable decompositions and overcomes the numerical pitfalls of prior art. Our method can handle possible challenging scenarios: (1) when calibration matrices exceed GPU memory capacity, (2) when input activation matrices are nearly singular, and even (3) when insufficient data prevents unique approximation. For the latter, we prove that our solution converges to a desired approximation and derive explicit error bounds.

Pay Attention to Attention Distribution: A New Local Lipschitz Bound for Transformers

We present a novel local Lipschitz bound for self-attention blocks of transformers. This bound is based on a refined closed-form expression for the spectral norm of the softmax function. The resulting bound is not only more accurate than in the prior art, but also unveils the dependence of the Lipschitz constant on attention score maps. Based on the new findings, we suggest an explanation of the way distributions inside the attention map affect the robustness from the Lipschitz constant perspective. We also introduce a new lightweight regularization term called JaSMin (Jacobian Softmax norm Minimization), which boosts the transformer's robustness and decreases local Lipschitz constants of the whole network.

On the Upper Bounds for the Matrix Spectral Norm

We consider the problem of estimating the spectral norm of a matrix using only matrix-vector products. We propose a new Counterbalance estimator that provides upper bounds on the norm and derive probabilistic guarantees on its underestimation. Compared to standard approaches such as the power method, the proposed estimator produces significantly tighter upper bounds in both synthetic and real-world settings. Our method is especially effective for matrices with fast-decaying spectra, such as those arising in deep learning and inverse problems.

Knowledge Graph Completion with Mixed Geometry Tensor Factorization

In this paper, we propose a new geometric approach for knowledge graph completion via low rank tensor approximation. We augment a pretrained and well-established Euclidean model based on a Tucker tensor decomposition with a novel hyperbolic interaction term. This correction enables more nuanced capturing of distributional properties in data better aligned with real-world knowledge graphs. By combining two geometries together, our approach improves expressivity of the resulting model achieving new state-of-the-art link prediction accuracy with a significantly lower number of parameters compared to the previous Euclidean and hyperbolic models.

Tight and Efficient Upper Bound on Spectral Norm of Convolutional Layers

Controlling the spectral norm of the Jacobian matrix, which is related to the convolution operation, has been shown to improve generalization, training stability and robustness in CNNs. Existing methods for computing the norm either tend to overestimate it or their performance may deteriorate quickly with increasing the input and kernel sizes. In this paper, we demonstrate that the tensor version of the spectral norm of a four-dimensional convolution kernel, up to a constant factor, serves as an upper bound for the spectral norm of the Jacobian matrix associated with the convolution operation. This new upper bound is independent of the input image resolution, differentiable and can be efficiently calculated during training. Through experiments, we demonstrate how this new bound can be used to improve the performance of convolutional architectures.

Group and Shuffle: Efficient Structured Orthogonal Parametrization

The increasing size of neural networks has led to a growing demand for methods of efficient fine-tuning. Recently, an orthogonal fine-tuning paradigm was introduced that uses orthogonal matrices for adapting the weights of a pretrained model. In this paper, we introduce a new class of structured matrices, which unifies and generalizes structured classes from previous works. We examine properties of this class and build a structured orthogonal parametrization upon it. We then use this parametrization to modify the orthogonal fine-tuning framework, improving parameter and computational efficiency. We empirically validate our method on different domains, including adapting of text-to-image diffusion models and downstream task fine-tuning in language modeling. Additionally, we adapt our construction for orthogonal convolutions and conduct experiments with 1-Lipschitz neural networks.

Dimension-free Structured Covariance Estimation

Given a sample of i.i.d. high-dimensional centered random vectors, we consider a problem of estimation of their covariance matrix $\Sigma$ with an additional assumption that $\Sigma$ can be represented as a sum of a few Kronecker products of smaller matrices. Under mild conditions, we derive the first non-asymptotic dimension-free high-probability bound on the Frobenius distance between $\Sigma$ and a widely used penalized permuted least squares estimate. Because of the hidden structure, the established rate of convergence is faster than in the standard covariance estimation problem.

Towards Practical Control of Singular Values of Convolutional Layers

In general, convolutional neural networks (CNNs) are easy to train, but their essential properties, such as generalization error and adversarial robustness, are hard to control. Recent research demonstrated that singular values of convolutional layers significantly affect such elusive properties and offered several methods for controlling them. Nevertheless, these methods present an intractable computational challenge or resort to coarse approximations. In this paper, we offer a principled approach to alleviating constraints of the prior art at the expense of an insignificant reduction in layer expressivity. Our method is based on the tensor-train decomposition; it retains control over the actual singular values of convolutional mappings while providing structurally sparse and hardware-friendly representation. We demonstrate the improved properties of modern CNNs with our method and analyze its impact on the model performance, calibration, and adversarial robustness. The source code is available at: https://github.com/WhiteTeaDragon/practical_svd_conv

Cherry-Picking Gradients: Learning Low-Rank Embeddings of Visual Data via Differentiable Cross-Approximation

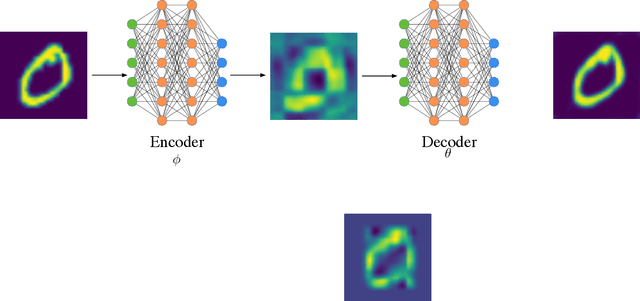
We propose an end-to-end trainable framework that processes large-scale visual data tensors by looking \emph{at a fraction of their entries only}. Our method combines a neural network encoder with a \emph{tensor train decomposition} to learn a low-rank latent encoding, coupled with cross-approximation (CA) to learn the representation through a subset of the original samples. CA is an adaptive sampling algorithm that is native to tensor decompositions and avoids working with the full high-resolution data explicitly. Instead, it actively selects local representative samples that we fetch out-of-core and on-demand. The required number of samples grows only logarithmically with the size of the input. Our implicit representation of the tensor in the network enables processing large grids that could not be otherwise tractable in their uncompressed form. The proposed approach is particularly useful for large-scale multidimensional grid data (e.g., 3D tomography), and for tasks that require context over a large receptive field (e.g., predicting the medical condition of entire organs). The code will be available at https://github.com/aelphy/c-pic