Lagrangian-based Equilibrium Propagation: generalisation to arbitrary boundary conditions & equivalence with Hamiltonian Echo Learning

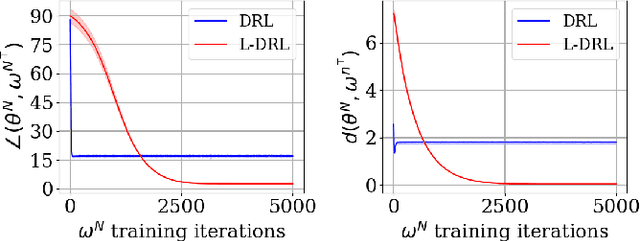
Equilibrium Propagation (EP) is a learning algorithm for training Energy-based Models (EBMs) on static inputs which leverages the variational description of their fixed points. Extending EP to time-varying inputs is a challenging problem, as the variational description must apply to the entire system trajectory rather than just fixed points, and careful consideration of boundary conditions becomes essential. In this work, we present Generalized Lagrangian Equilibrium Propagation (GLEP), which extends the variational formulation of EP to time-varying inputs. We demonstrate that GLEP yields different learning algorithms depending on the boundary conditions of the system, many of which are impractical for implementation. We then show that Hamiltonian Echo Learning (HEL) -- which includes the recently proposed Recurrent HEL (RHEL) and the earlier known Hamiltonian Echo Backpropagation (HEB) algorithms -- can be derived as a special case of GLEP. Notably, HEL is the only instance of GLEP we found that inherits the properties that make EP a desirable alternative to backpropagation for hardware implementations: it operates in a "forward-only" manner (i.e. using the same system for both inference and learning), it scales efficiently (requiring only two or more passes through the system regardless of model size), and enables local learning.

Learning long range dependencies through time reversal symmetry breaking

Deep State Space Models (SSMs) reignite physics-grounded compute paradigms, as RNNs could natively be embodied into dynamical systems. This calls for dedicated learning algorithms obeying to core physical principles, with efficient techniques to simulate these systems and guide their design. We propose Recurrent Hamiltonian Echo Learning (RHEL), an algorithm which provably computes loss gradients as finite differences of physical trajectories of non-dissipative, Hamiltonian systems. In ML terms, RHEL only requires three "forward passes" irrespective of model size, without explicit Jacobian computation, nor incurring any variance in the gradient estimation. Motivated by the physical realization of our algorithm, we first introduce RHEL in continuous time and demonstrate its formal equivalence with the continuous adjoint state method. To facilitate the simulation of Hamiltonian systems trained by RHEL, we propose a discrete-time version of RHEL which is equivalent to Backpropagation Through Time (BPTT) when applied to a class of recurrent modules which we call Hamiltonian Recurrent Units (HRUs). This setting allows us to demonstrate the scalability of RHEL by generalizing these results to hierarchies of HRUs, which we call Hamiltonian SSMs (HSSMs). We apply RHEL to train HSSMs with linear and nonlinear dynamics on a variety of time-series tasks ranging from mid-range to long-range classification and regression with sequence length reaching $\sim 50k$. We show that RHEL consistently matches the performance of BPTT across all models and tasks. This work opens new doors for the design of scalable, energy-efficient physical systems endowed with self-learning capabilities for sequence modelling.

Towards training digitally-tied analog blocks via hybrid gradient computation

Power efficiency is plateauing in the standard digital electronics realm such that novel hardware, models, and algorithms are needed to reduce the costs of AI training. The combination of energy-based analog circuits and the Equilibrium Propagation (EP) algorithm constitutes one compelling alternative compute paradigm for gradient-based optimization of neural nets. Existing analog hardware accelerators, however, typically incorporate digital circuitry to sustain auxiliary non-weight-stationary operations, mitigate analog device imperfections, and leverage existing digital accelerators.This heterogeneous hardware approach calls for a new theoretical model building block. In this work, we introduce Feedforward-tied Energy-based Models (ff-EBMs), a hybrid model comprising feedforward and energy-based blocks accounting for digital and analog circuits. We derive a novel algorithm to compute gradients end-to-end in ff-EBMs by backpropagating and "eq-propagating" through feedforward and energy-based parts respectively, enabling EP to be applied to much more flexible and realistic architectures. We experimentally demonstrate the effectiveness of the proposed approach on ff-EBMs where Deep Hopfield Networks (DHNs) are used as energy-based blocks. We first show that a standard DHN can be arbitrarily split into any uniform size while maintaining performance. We then train ff-EBMs on ImageNet32 where we establish new SOTA performance in the EP literature (46 top-1 %). Our approach offers a principled, scalable, and incremental roadmap to gradually integrate self-trainable analog computational primitives into existing digital accelerators.

Energy-based learning algorithms for analog computing: a comparative study

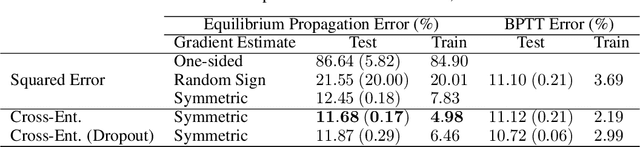
Energy-based learning algorithms have recently gained a surge of interest due to their compatibility with analog (post-digital) hardware. Existing algorithms include contrastive learning (CL), equilibrium propagation (EP) and coupled learning (CpL), all consisting in contrasting two states, and differing in the type of perturbation used to obtain the second state from the first one. However, these algorithms have never been explicitly compared on equal footing with same models and datasets, making it difficult to assess their scalability and decide which one to select in practice. In this work, we carry out a comparison of seven learning algorithms, namely CL and different variants of EP and CpL depending on the signs of the perturbations. Specifically, using these learning algorithms, we train deep convolutional Hopfield networks (DCHNs) on five vision tasks (MNIST, F-MNIST, SVHN, CIFAR-10 and CIFAR-100). We find that, while all algorithms yield comparable performance on MNIST, important differences in performance arise as the difficulty of the task increases. Our key findings reveal that negative perturbations are better than positive ones, and highlight the centered variant of EP (which uses two perturbations of opposite sign) as the best-performing algorithm. We also endorse these findings with theoretical arguments. Additionally, we establish new SOTA results with DCHNs on all five datasets, both in performance and speed. In particular, our DCHN simulations are 13.5 times faster with respect to Laborieux et al. (2021), which we achieve thanks to the use of a novel energy minimisation algorithm based on asynchronous updates, combined with reduced precision (16 bits).

Towards Scaling Difference Target Propagation by Learning Backprop Targets

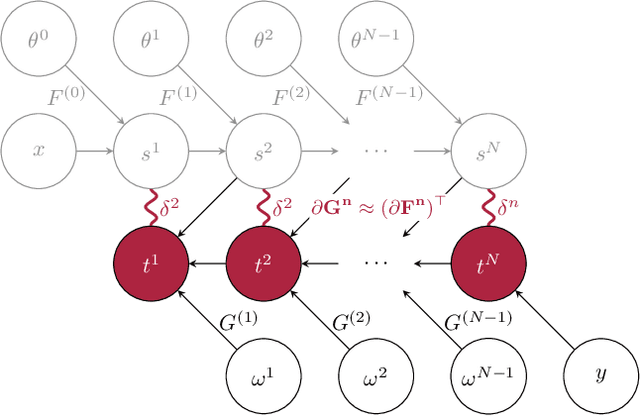
The development of biologically-plausible learning algorithms is important for understanding learning in the brain, but most of them fail to scale-up to real-world tasks, limiting their potential as explanations for learning by real brains. As such, it is important to explore learning algorithms that come with strong theoretical guarantees and can match the performance of backpropagation (BP) on complex tasks. One such algorithm is Difference Target Propagation (DTP), a biologically-plausible learning algorithm whose close relation with Gauss-Newton (GN) optimization has been recently established. However, the conditions under which this connection rigorously holds preclude layer-wise training of the feedback pathway synaptic weights (which is more biologically plausible). Moreover, good alignment between DTP weight updates and loss gradients is only loosely guaranteed and under very specific conditions for the architecture being trained. In this paper, we propose a novel feedback weight training scheme that ensures both that DTP approximates BP and that layer-wise feedback weight training can be restored without sacrificing any theoretical guarantees. Our theory is corroborated by experimental results and we report the best performance ever achieved by DTP on CIFAR-10 and ImageNet 32$\times$32

Training Dynamical Binary Neural Networks with Equilibrium Propagation

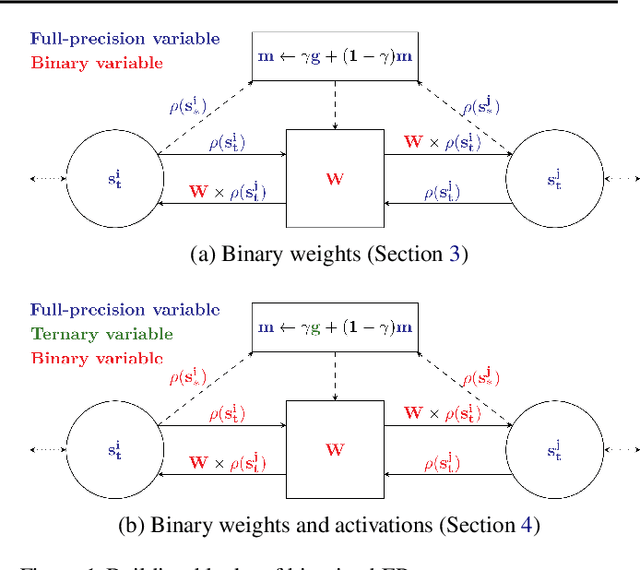
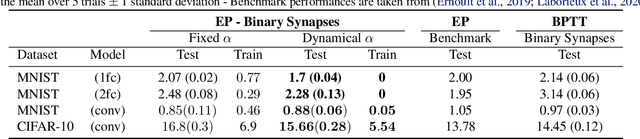
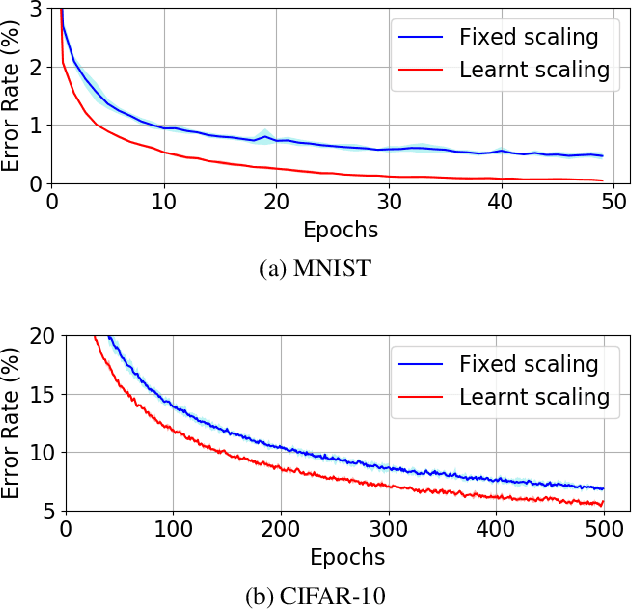
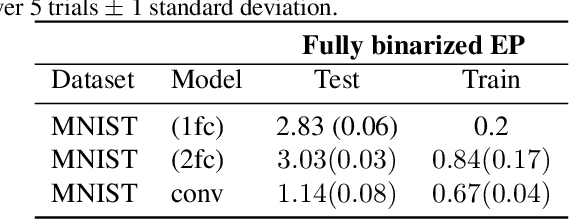
Equilibrium Propagation (EP) is an algorithm intrinsically adapted to the training of physical networks, in particular thanks to the local updates of weights given by the internal dynamics of the system. However, the construction of such a hardware requires to make the algorithm compatible with the existing neuromorphic CMOS technology, which generally exploits digital communication between neurons and offers a limited amount of local memory. In this work, we demonstrate that EP can train dynamical networks with binary activations and weights. We first train systems with binary weights and full-precision activations, achieving an accuracy equivalent to that of full-precision models trained by standard EP on MNIST, and losing only 1.9% accuracy on CIFAR-10 with equal architecture. We then extend our method to the training of models with binary activations and weights on MNIST, achieving an accuracy within 1% of the full-precision reference for fully connected architectures and reaching the full-precision reference accuracy for the convolutional architecture. Our extension of EP training to binary networks is consistent with the requirements of today's dynamic, brain-inspired hardware platforms and paves the way for very low-power end-to-end learning.

Synaptic metaplasticity in binarized neural networks

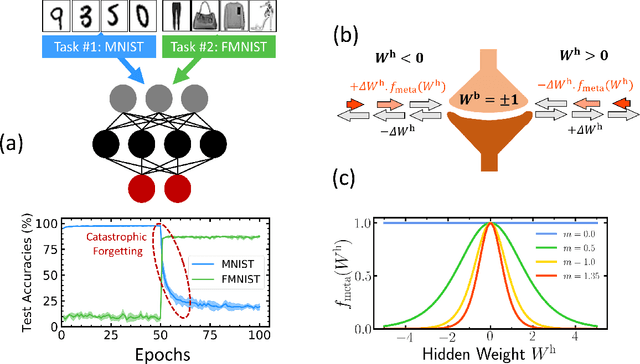
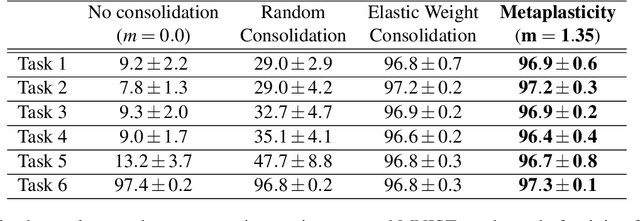
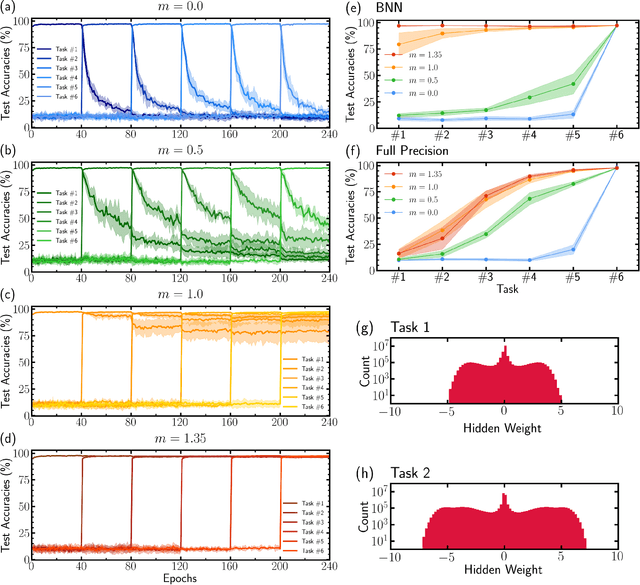
Unlike the brain, artificial neural networks, including state-of-the-art deep neural networks for computer vision, are subject to "catastrophic forgetting": they rapidly forget the previous task when trained on a new one. Neuroscience suggests that biological synapses avoid this issue through the process of synaptic consolidation and metaplasticity: the plasticity itself changes upon repeated synaptic events. In this work, we show that this concept of metaplasticity can be transferred to a particular type of deep neural networks, binarized neural networks, to reduce catastrophic forgetting.

Scaling Equilibrium Propagation to Deep ConvNets by Drastically Reducing its Gradient Estimator Bias

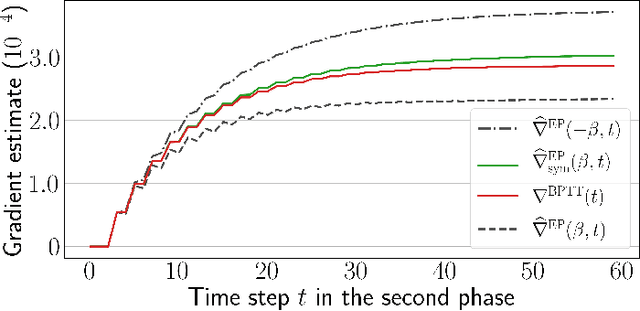
Equilibrium Propagation (EP) is a biologically-inspired counterpart of Backpropagation Through Time (BPTT) which, owing to its strong theoretical guarantees and the locality in space of its learning rule, fosters the design of energy-efficient hardware dedicated to learning. In practice, however, EP does not scale to visual tasks harder than MNIST. In this work, we show that a bias in the gradient estimate of EP, inherent in the use of finite nudging, is responsible for this phenomenon and that cancelling it allows training deep ConvNets by EP, including architectures with distinct forward and backward connections. These results highlight EP as a scalable approach to compute error gradients in deep neural networks, thereby motivating its hardware implementation.

EqSpike: Spike-driven Equilibrium Propagation for Neuromorphic Implementations

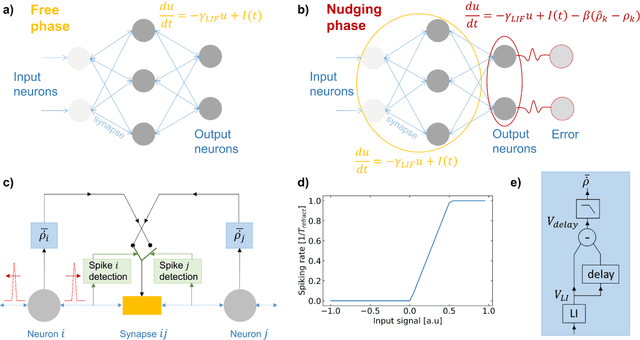
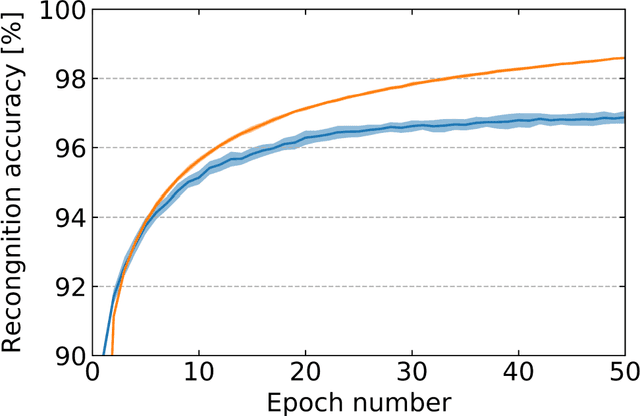
Neuromorphic systems achieve high energy efficiency by computing with spikes, in a brain-inspired way. However, finding spike-based learning algorithms that can be implemented within the local constraints of neuromorphic systems, while achieving high accuracy, remains a formidable challenge. Equilibrium Propagation is a hardware-friendly counterpart of backpropagation which only involves spatially local computations and applies to recurrent neural networks with static inputs. So far, hardware-oriented studies of Equilibrium Propagation focused on rate-based networks. In this work, we develop a spiking neural network algorithm called EqSpike, compatible with neuromorphic systems, which learns by Equilibrium Propagation. Through simulations, we obtain a test recognition accuracy of 96.9% on MNIST, similar to rate-based Equilibrium Propagation, and comparing favourably to alternative learning techniques for spiking neural networks. We show that EqSpike implemented in silicon neuromorphic technology could reduce the energy consumption of inference and training by up to three orders of magnitude compared to GPUs. Finally, we also show that during learning, EqSpike weight updates exhibit a form of Spike Timing Dependent Plasticity, highlighting a possible connection with biology.

Equilibrium Propagation with Continual Weight Updates

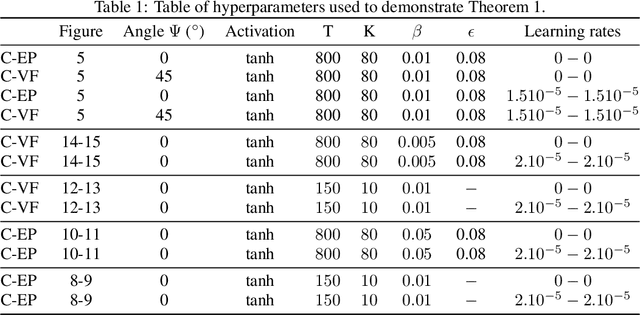
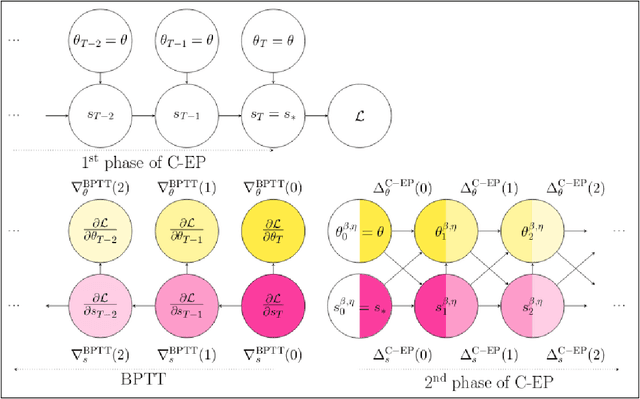
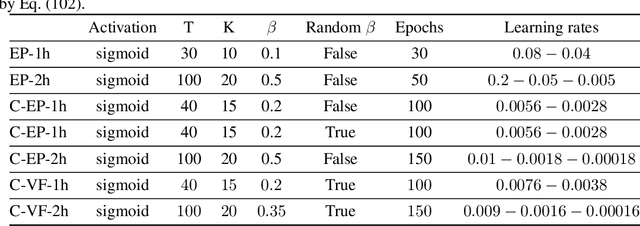
Equilibrium Propagation (EP) is a learning algorithm that bridges Machine Learning and Neuroscience, by computing gradients closely matching those of Backpropagation Through Time (BPTT), but with a learning rule local in space. Given an input $x$ and associated target $y$, EP proceeds in two phases: in the first phase neurons evolve freely towards a first steady state; in the second phase output neurons are nudged towards $y$ until they reach a second steady state. However, in existing implementations of EP, the learning rule is not local in time: the weight update is performed after the dynamics of the second phase have converged and requires information of the first phase that is no longer available physically. In this work, we propose a version of EP named Continual Equilibrium Propagation (C-EP) where neuron and synapse dynamics occur simultaneously throughout the second phase, so that the weight update becomes local in time. Such a learning rule local both in space and time opens the possibility of an extremely energy efficient hardware implementation of EP. We prove theoretically that, provided the learning rates are sufficiently small, at each time step of the second phase the dynamics of neurons and synapses follow the gradients of the loss given by BPTT (Theorem 1). We demonstrate training with C-EP on MNIST and generalize C-EP to neural networks where neurons are connected by asymmetric connections. We show through experiments that the more the network updates follows the gradients of BPTT, the best it performs in terms of training. These results bring EP a step closer to biology by better complying with hardware constraints while maintaining its intimate link with backpropagation.