Lagrangian-based Equilibrium Propagation: generalisation to arbitrary boundary conditions & equivalence with Hamiltonian Echo Learning

Equilibrium Propagation (EP) is a learning algorithm for training Energy-based Models (EBMs) on static inputs which leverages the variational description of their fixed points. Extending EP to time-varying inputs is a challenging problem, as the variational description must apply to the entire system trajectory rather than just fixed points, and careful consideration of boundary conditions becomes essential. In this work, we present Generalized Lagrangian Equilibrium Propagation (GLEP), which extends the variational formulation of EP to time-varying inputs. We demonstrate that GLEP yields different learning algorithms depending on the boundary conditions of the system, many of which are impractical for implementation. We then show that Hamiltonian Echo Learning (HEL) -- which includes the recently proposed Recurrent HEL (RHEL) and the earlier known Hamiltonian Echo Backpropagation (HEB) algorithms -- can be derived as a special case of GLEP. Notably, HEL is the only instance of GLEP we found that inherits the properties that make EP a desirable alternative to backpropagation for hardware implementations: it operates in a "forward-only" manner (i.e. using the same system for both inference and learning), it scales efficiently (requiring only two or more passes through the system regardless of model size), and enables local learning.

Learning long range dependencies through time reversal symmetry breaking

Deep State Space Models (SSMs) reignite physics-grounded compute paradigms, as RNNs could natively be embodied into dynamical systems. This calls for dedicated learning algorithms obeying to core physical principles, with efficient techniques to simulate these systems and guide their design. We propose Recurrent Hamiltonian Echo Learning (RHEL), an algorithm which provably computes loss gradients as finite differences of physical trajectories of non-dissipative, Hamiltonian systems. In ML terms, RHEL only requires three "forward passes" irrespective of model size, without explicit Jacobian computation, nor incurring any variance in the gradient estimation. Motivated by the physical realization of our algorithm, we first introduce RHEL in continuous time and demonstrate its formal equivalence with the continuous adjoint state method. To facilitate the simulation of Hamiltonian systems trained by RHEL, we propose a discrete-time version of RHEL which is equivalent to Backpropagation Through Time (BPTT) when applied to a class of recurrent modules which we call Hamiltonian Recurrent Units (HRUs). This setting allows us to demonstrate the scalability of RHEL by generalizing these results to hierarchies of HRUs, which we call Hamiltonian SSMs (HSSMs). We apply RHEL to train HSSMs with linear and nonlinear dynamics on a variety of time-series tasks ranging from mid-range to long-range classification and regression with sequence length reaching $\sim 50k$. We show that RHEL consistently matches the performance of BPTT across all models and tasks. This work opens new doors for the design of scalable, energy-efficient physical systems endowed with self-learning capabilities for sequence modelling.

Adaptive control of recurrent neural networks using conceptors

Recurrent Neural Networks excel at predicting and generating complex high-dimensional temporal patterns. Due to their inherent nonlinear dynamics and memory, they can learn unbounded temporal dependencies from data. In a Machine Learning setting, the network's parameters are adapted during a training phase to match the requirements of a given task/problem increasing its computational capabilities. After the training, the network parameters are kept fixed to exploit the learned computations. The static parameters thereby render the network unadaptive to changing conditions, such as external or internal perturbation. In this manuscript, we demonstrate how keeping parts of the network adaptive even after the training enhances its functionality and robustness. Here, we utilize the conceptor framework and conceptualize an adaptive control loop analyzing the network's behavior continuously and adjusting its time-varying internal representation to follow a desired target. We demonstrate how the added adaptivity of the network supports the computational functionality in three distinct tasks: interpolation of temporal patterns, stabilization against partial network degradation, and robustness against input distortion. Our results highlight the potential of adaptive networks in machine learning beyond training, enabling them to not only learn complex patterns but also dynamically adjust to changing environments, ultimately broadening their applicability.

How to reduce computation time while sparing performance during robot navigation? A neuro-inspired architecture for autonomous shifting between model-based and model-free learning

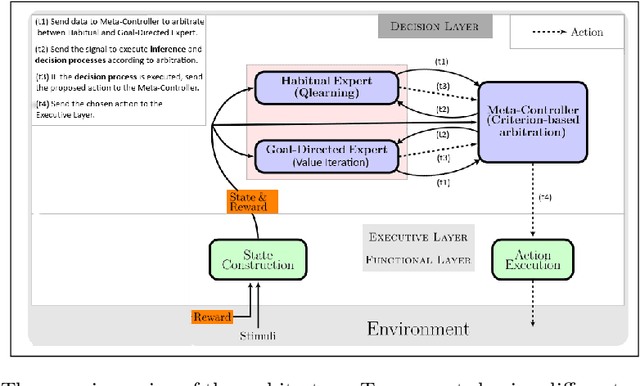
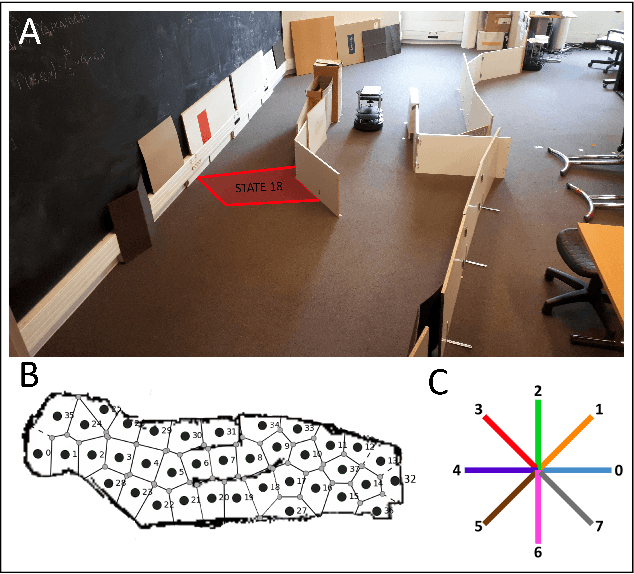
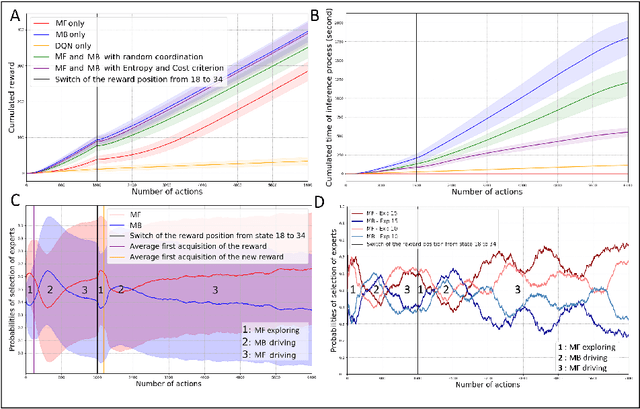
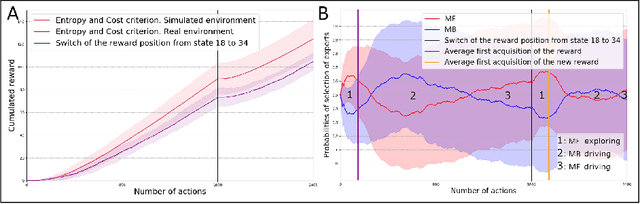
Taking inspiration from how the brain coordinates multiple learning systems is an appealing strategy to endow robots with more flexibility. One of the expected advantages would be for robots to autonomously switch to the least costly system when its performance is satisfying. However, to our knowledge no study on a real robot has yet shown that the measured computational cost is reduced while performance is maintained with such brain-inspired algorithms. We present navigation experiments involving paths of different lengths to the goal, dead-end, and non-stationarity (i.e., change in goal location and apparition of obstacles). We present a novel arbitration mechanism between learning systems that explicitly measures performance and cost. We find that the robot can adapt to environment changes by switching between learning systems so as to maintain a high performance. Moreover, when the task is stable, the robot also autonomously shifts to the least costly system, which leads to a drastic reduction in computation cost while keeping a high performance. Overall, these results illustrates the interest of using multiple learning systems.