Probabilistic Performance Guarantees for Multi-Task Reinforcement Learning

Multi-task reinforcement learning trains generalist policies that can execute multiple tasks. While recent years have seen significant progress, existing approaches rarely provide formal performance guarantees, which are indispensable when deploying policies in safety-critical settings. We present an approach for computing high-confidence guarantees on the performance of a multi-task policy on tasks not seen during training. Concretely, we introduce a new generalisation bound that composes (i) per-task lower confidence bounds from finitely many rollouts with (ii) task-level generalisation from finitely many sampled tasks, yielding a high-confidence guarantee for new tasks drawn from the same arbitrary and unknown distribution. Across state-of-the-art multi-task RL methods, we show that the guarantees are theoretically sound and informative at realistic sample sizes.

PlatoLTL: Learning to Generalize Across Symbols in LTL Instructions for Multi-Task RL

A central challenge in multi-task reinforcement learning (RL) is to train generalist policies capable of performing tasks not seen during training. To facilitate such generalization, linear temporal logic (LTL) has recently emerged as a powerful formalism for specifying structured, temporally extended tasks to RL agents. While existing approaches to LTL-guided multi-task RL demonstrate successful generalization across LTL specifications, they are unable to generalize to unseen vocabularies of propositions (or "symbols"), which describe high-level events in LTL. We present PlatoLTL, a novel approach that enables policies to zero-shot generalize not only compositionally across LTL formula structures, but also parametrically across propositions. We achieve this by treating propositions as instances of parameterized predicates rather than discrete symbols, allowing policies to learn shared structure across related propositions. We propose a novel architecture that embeds and composes predicates to represent LTL specifications, and demonstrate successful zero-shot generalization to novel propositions and tasks across challenging environments.

DeepLTL: Learning to Efficiently Satisfy Complex LTL Specifications

Linear temporal logic (LTL) has recently been adopted as a powerful formalism for specifying complex, temporally extended tasks in reinforcement learning (RL). However, learning policies that efficiently satisfy arbitrary specifications not observed during training remains a challenging problem. Existing approaches suffer from several shortcomings: they are often only applicable to finite-horizon fragments of LTL, are restricted to suboptimal solutions, and do not adequately handle safety constraints. In this work, we propose a novel learning approach to address these concerns. Our method leverages the structure of B\"uchi automata, which explicitly represent the semantics of LTL specifications, to learn policies conditioned on sequences of truth assignments that lead to satisfying the desired formulae. Experiments in a variety of discrete and continuous domains demonstrate that our approach is able to zero-shot satisfy a wide range of finite- and infinite-horizon specifications, and outperforms existing methods in terms of both satisfaction probability and efficiency.

Box$^2$EL: Concept and Role Box Embeddings for the Description Logic EL++

Representation learning in the form of semantic embeddings has been successfully applied to a variety of tasks in natural language processing and knowledge graphs. Recently, there has been growing interest in developing similar methods for learning embeddings of entire ontologies. We propose Box$^2$EL, a novel method for representation learning of ontologies in the Description Logic EL++, which represents both concepts and roles as boxes (i.e. axis-aligned hyperrectangles), such that the logical structure of the ontology is preserved. We theoretically prove the soundness of our model and conduct an extensive empirical evaluation, in which we achieve state-of-the-art results in subsumption prediction, link prediction, and deductive reasoning. As part of our evaluation, we introduce a novel benchmark for evaluating EL++ embedding models on predicting subsumptions involving both atomic and complex concepts.

dtControl 2.0: Explainable Strategy Representation via Decision Tree Learning Steered by Experts

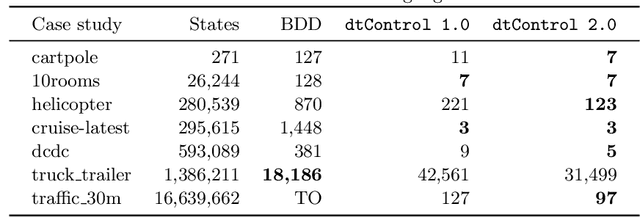
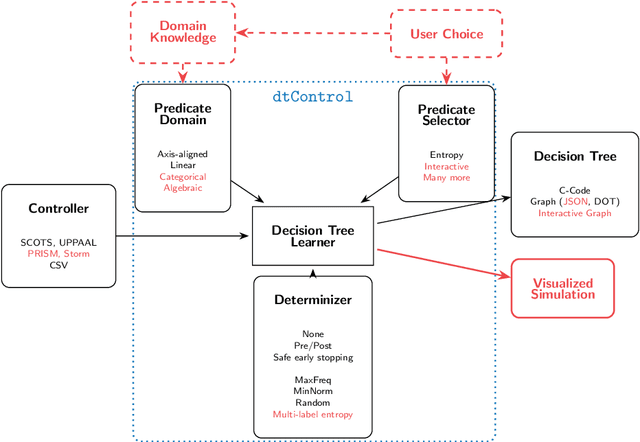
Recent advances have shown how decision trees are apt data structures for concisely representing strategies (or controllers) satisfying various objectives. Moreover, they also make the strategy more explainable. The recent tool dtControl had provided pipelines with tools supporting strategy synthesis for hybrid systems, such as SCOTS and Uppaal Stratego. We present dtControl 2.0, a new version with several fundamentally novel features. Most importantly, the user can now provide domain knowledge to be exploited in the decision tree learning process and can also interactively steer the process based on the dynamically provided information. To this end, we also provide a graphical user interface. It allows for inspection and re-computation of parts of the result, suggesting as well as receiving advice on predicates, and visual simulation of the decision-making process. Besides, we interface model checkers of probabilistic systems, namely Storm and PRISM and provide dedicated support for categorical enumeration-type state variables. Consequently, the controllers are more explainable and smaller.

dtControl: Decision Tree Learning Algorithms for Controller Representation

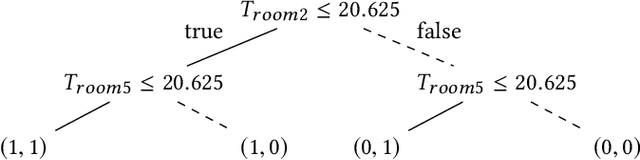
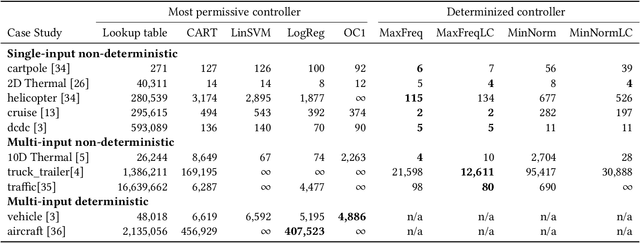
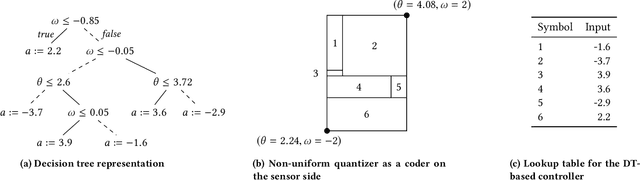
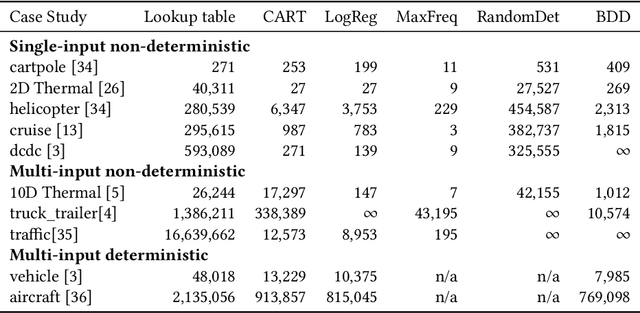
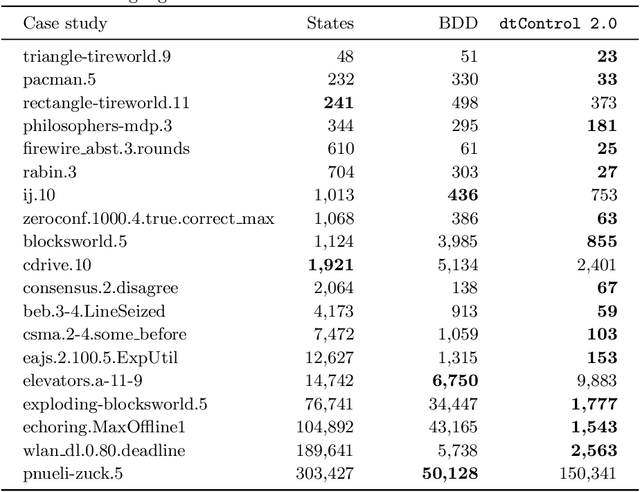
Decision tree learning is a popular classification technique most commonly used in machine learning applications. Recent work has shown that decision trees can be used to represent provably-correct controllers concisely. Compared to representations using lookup tables or binary decision diagrams, decision trees are smaller and more explainable. We present dtControl, an easily extensible tool for representing memoryless controllers as decision trees. We give a comprehensive evaluation of various decision tree learning algorithms applied to 10 case studies arising out of correct-by-construction controller synthesis. These algorithms include two new techniques, one for using arbitrary linear binary classifiers in the decision tree learning, and one novel approach for determinizing controllers during the decision tree construction. In particular the latter turns out to be extremely efficient, yielding decision trees with a single-digit number of decision nodes on 5 of the case studies.