Asymptotic Normality of Infinite Centered Random Forests -Application to Imbalanced Classification

Many classification tasks involve imbalanced data, in which a class is largely underrepresented. Several techniques consists in creating a rebalanced dataset on which a classifier is trained. In this paper, we study theoretically such a procedure, when the classifier is a Centered Random Forests (CRF). We establish a Central Limit Theorem (CLT) on the infinite CRF with explicit rates and exact constant. We then prove that the CRF trained on the rebalanced dataset exhibits a bias, which can be removed with appropriate techniques. Based on an importance sampling (IS) approach, the resulting debiased estimator, called IS-ICRF, satisfies a CLT centered at the prediction function value. For high imbalance settings, we prove that the IS-ICRF estimator enjoys a variance reduction compared to the ICRF trained on the original data. Therefore, our theoretical analysis highlights the benefits of training random forests on a rebalanced dataset (followed by a debiasing procedure) compared to using the original data. Our theoretical results, especially the variance rates and the variance reduction, appear to be valid for Breiman's random forests in our experiments.

Weighted Empirical Risk Minimization: Sample Selection Bias Correction based on Importance Sampling

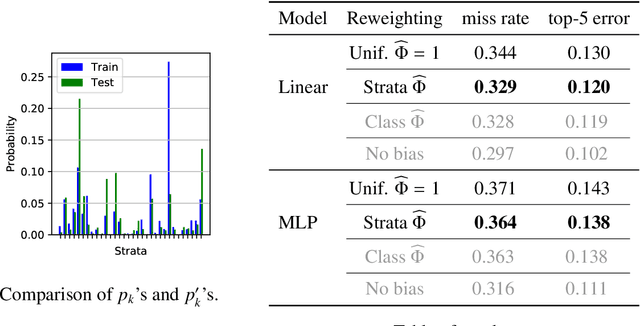
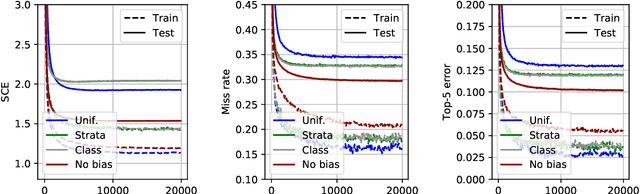
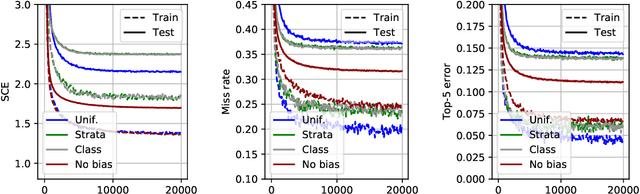
We consider statistical learning problems, when the distribution $P'$ of the training observations $Z'_1,\; \ldots,\; Z'_n$ differs from the distribution $P$ involved in the risk one seeks to minimize (referred to as the test distribution) but is still defined on the same measurable space as $P$ and dominates it. In the unrealistic case where the likelihood ratio $\Phi(z)=dP/dP'(z)$ is known, one may straightforwardly extends the Empirical Risk Minimization (ERM) approach to this specific transfer learning setup using the same idea as that behind Importance Sampling, by minimizing a weighted version of the empirical risk functional computed from the 'biased' training data $Z'_i$ with weights $\Phi(Z'_i)$. Although the importance function $\Phi(z)$ is generally unknown in practice, we show that, in various situations frequently encountered in practice, it takes a simple form and can be directly estimated from the $Z'_i$'s and some auxiliary information on the statistical population $P$. By means of linearization techniques, we then prove that the generalization capacity of the approach aforementioned is preserved when plugging the resulting estimates of the $\Phi(Z'_i)$'s into the weighted empirical risk. Beyond these theoretical guarantees, numerical results provide strong empirical evidence of the relevance of the approach promoted in this article.