Generalization Bounds for Transfer Learning with Pretrained Classifiers

We study the ability of foundation models to learn representations for classification that are transferable to new, unseen classes. Recent results in the literature show that representations learned by a single classifier over many classes are competitive on few-shot learning problems with representations learned by special-purpose algorithms designed for such problems. We offer an explanation for this phenomenon based on the concept of class-features variability collapse, which refers to the training dynamics of deep classification networks where the feature embeddings of samples belonging to the same class tend to concentrate around their class means. More specifically, we examine the few-shot error of the learned feature map, which is the classification error of the nearest class-center classifier using centers learned from a small number of random samples from each class. Assuming that the classes appearing in the data are selected independently from a distribution, we show that the few-shot error generalizes from the training data to unseen test data, and we provide an upper bound on the expected few-shot error for new classes (selected from the same distribution) using the average few-shot error for the source classes. Additionally, we show that the few-shot error on the training data can be upper bounded using the degree of class-features variability collapse. This suggests that foundation models can provide feature maps that are transferable to new downstream tasks even with limited data available.

Sequential Learning Of Neural Networks for Prequential MDL

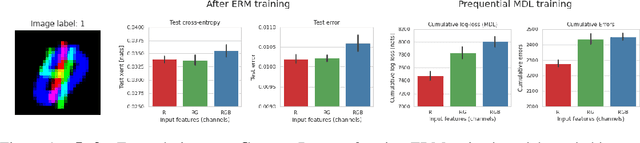
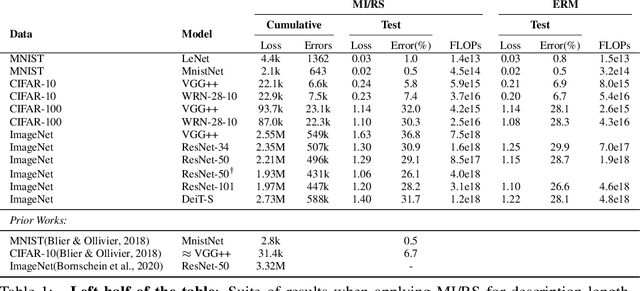
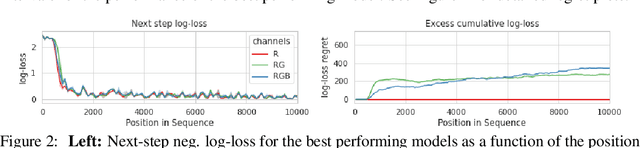
Minimum Description Length (MDL) provides a framework and an objective for principled model evaluation. It formalizes Occam's Razor and can be applied to data from non-stationary sources. In the prequential formulation of MDL, the objective is to minimize the cumulative next-step log-loss when sequentially going through the data and using previous observations for parameter estimation. It thus closely resembles a continual- or online-learning problem. In this study, we evaluate approaches for computing prequential description lengths for image classification datasets with neural networks. Considering the computational cost, we find that online-learning with rehearsal has favorable performance compared to the previously widely used block-wise estimation. We propose forward-calibration to better align the models predictions with the empirical observations and introduce replay-streams, a minibatch incremental training technique to efficiently implement approximate random replay while avoiding large in-memory replay buffers. As a result, we present description lengths for a suite of image classification datasets that improve upon previously reported results by large margins.

Beyond Bayes-optimality: meta-learning what you know you don't know

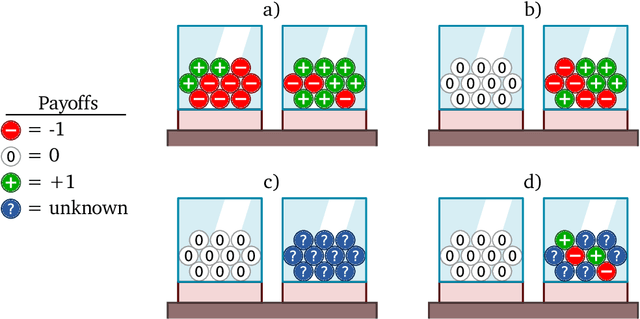
Meta-training agents with memory has been shown to culminate in Bayes-optimal agents, which casts Bayes-optimality as the implicit solution to a numerical optimization problem rather than an explicit modeling assumption. Bayes-optimal agents are risk-neutral, since they solely attune to the expected return, and ambiguity-neutral, since they act in new situations as if the uncertainty were known. This is in contrast to risk-sensitive agents, which additionally exploit the higher-order moments of the return, and ambiguity-sensitive agents, which act differently when recognizing situations in which they lack knowledge. Humans are also known to be averse to ambiguity and sensitive to risk in ways that aren't Bayes-optimal, indicating that such sensitivity can confer advantages, especially in safety-critical situations. How can we extend the meta-learning protocol to generate risk- and ambiguity-sensitive agents? The goal of this work is to fill this gap in the literature by showing that risk- and ambiguity-sensitivity also emerge as the result of an optimization problem using modified meta-training algorithms, which manipulate the experience-generation process of the learner. We empirically test our proposed meta-training algorithms on agents exposed to foundational classes of decision-making experiments and demonstrate that they become sensitive to risk and ambiguity.

Atari-5: Distilling the Arcade Learning Environment down to Five Games

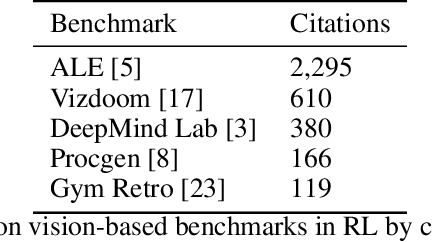
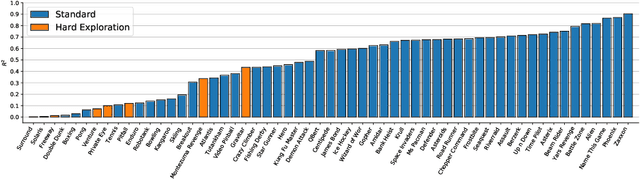
The Arcade Learning Environment (ALE) has become an essential benchmark for assessing the performance of reinforcement learning algorithms. However, the computational cost of generating results on the entire 57-game dataset limits ALE's use and makes the reproducibility of many results infeasible. We propose a novel solution to this problem in the form of a principled methodology for selecting small but representative subsets of environments within a benchmark suite. We applied our method to identify a subset of five ALE games, called Atari-5, which produces 57-game median score estimates within 10% of their true values. Extending the subset to 10-games recovers 80% of the variance for log-scores for all games within the 57-game set. We show this level of compression is possible due to a high degree of correlation between many of the games in ALE.

Formal Algorithms for Transformers

This document aims to be a self-contained, mathematically precise overview of transformer architectures and algorithms (*not* results). It covers what transformers are, how they are trained, what they are used for, their key architectural components, and a preview of the most prominent models. The reader is assumed to be familiar with basic ML terminology and simpler neural network architectures such as MLPs.

Neural Networks and the Chomsky Hierarchy

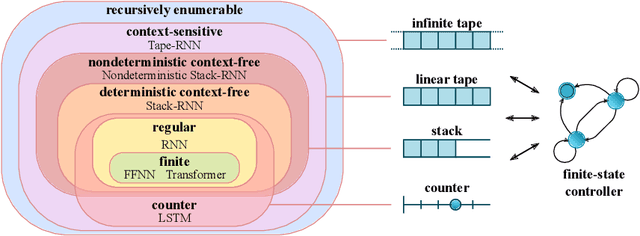
Reliable generalization lies at the heart of safe ML and AI. However, understanding when and how neural networks generalize remains one of the most important unsolved problems in the field. In this work, we conduct an extensive empirical study (2200 models, 16 tasks) to investigate whether insights from the theory of computation can predict the limits of neural network generalization in practice. We demonstrate that grouping tasks according to the Chomsky hierarchy allows us to forecast whether certain architectures will be able to generalize to out-of-distribution inputs. This includes negative results where even extensive amounts of data and training time never led to any non-trivial generalization, despite models having sufficient capacity to perfectly fit the training data. Our results show that, for our subset of tasks, RNNs and Transformers fail to generalize on non-regular tasks, LSTMs can solve regular and counter-language tasks, and only networks augmented with structured memory (such as a stack or memory tape) can successfully generalize on context-free and context-sensitive tasks.

Uniqueness and Complexity of Inverse MDP Models

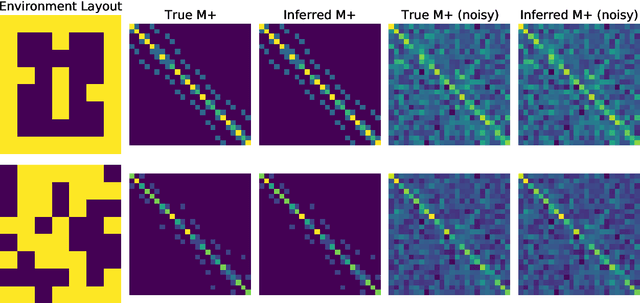
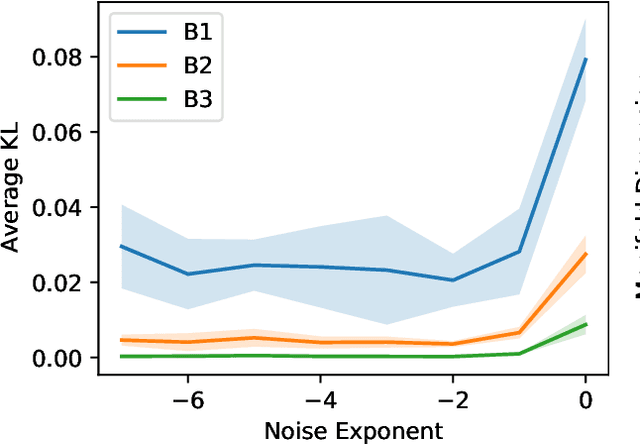
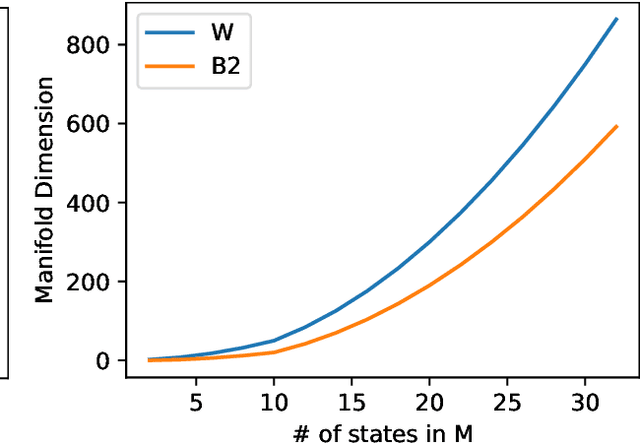
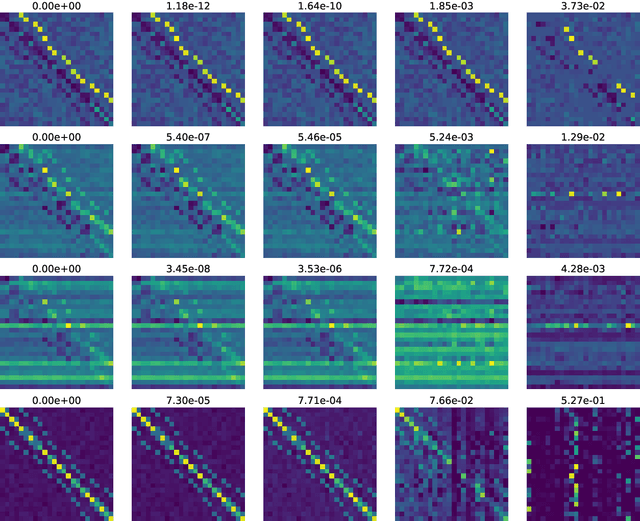
What is the action sequence aa'a" that was likely responsible for reaching state s"' (from state s) in 3 steps? Addressing such questions is important in causal reasoning and in reinforcement learning. Inverse "MDP" models p(aa'a"|ss"') can be used to answer them. In the traditional "forward" view, transition "matrix" p(s'|sa) and policy {\pi}(a|s) uniquely determine "everything": the whole dynamics p(as'a's"a"...|s), and with it, the action-conditional state process p(s's"...|saa'a"), the multi-step inverse models p(aa'a"...|ss^i), etc. If the latter is our primary concern, a natural question, analogous to the forward case is to which extent 1-step inverse model p(a|ss') plus policy {\pi}(a|s) determine the multi-step inverse models or even the whole dynamics. In other words, can forward models be inferred from inverse models or even be side-stepped. This work addresses this question and variations thereof, and also whether there are efficient decision/inference algorithms for this.

On the Role of Neural Collapse in Transfer Learning

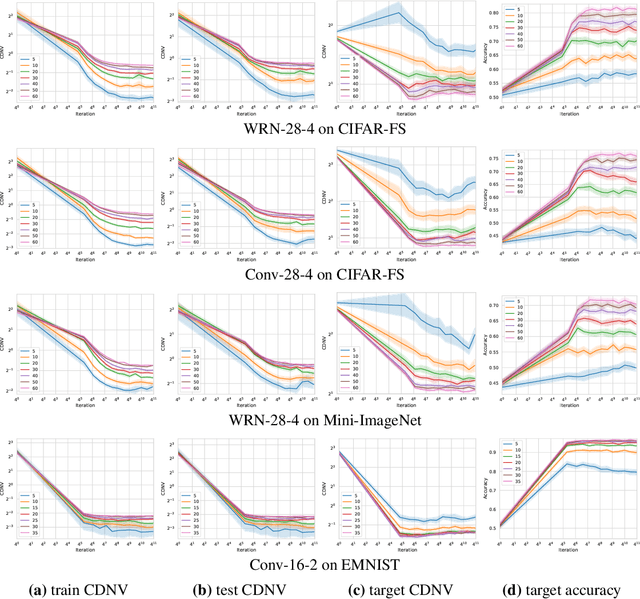
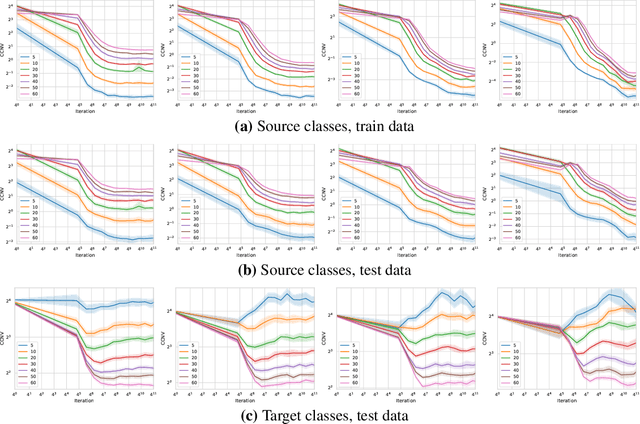
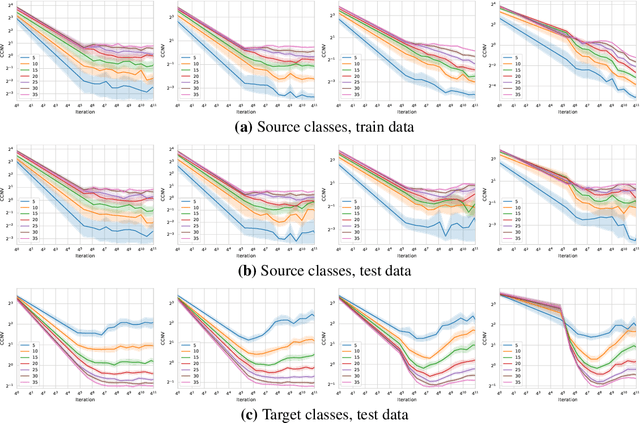
We study the ability of foundation models to learn representations for classification that are transferable to new, unseen classes. Recent results in the literature show that representations learned by a single classifier over many classes are competitive on few-shot learning problems with representations learned by special-purpose algorithms designed for such problems. In this paper we provide an explanation for this behavior based on the recently observed phenomenon that the features learned by overparameterized classification networks show an interesting clustering property, called neural collapse. We demonstrate both theoretically and empirically that neural collapse generalizes to new samples from the training classes, and -- more importantly -- to new classes as well, allowing foundation models to provide feature maps that work well in transfer learning and, specifically, in the few-shot setting.

Isotuning With Applications To Scale-Free Online Learning

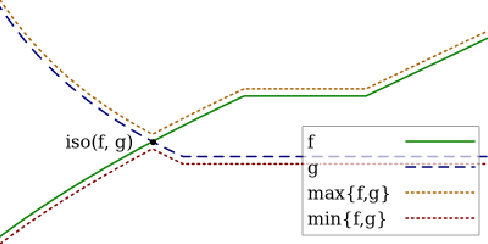
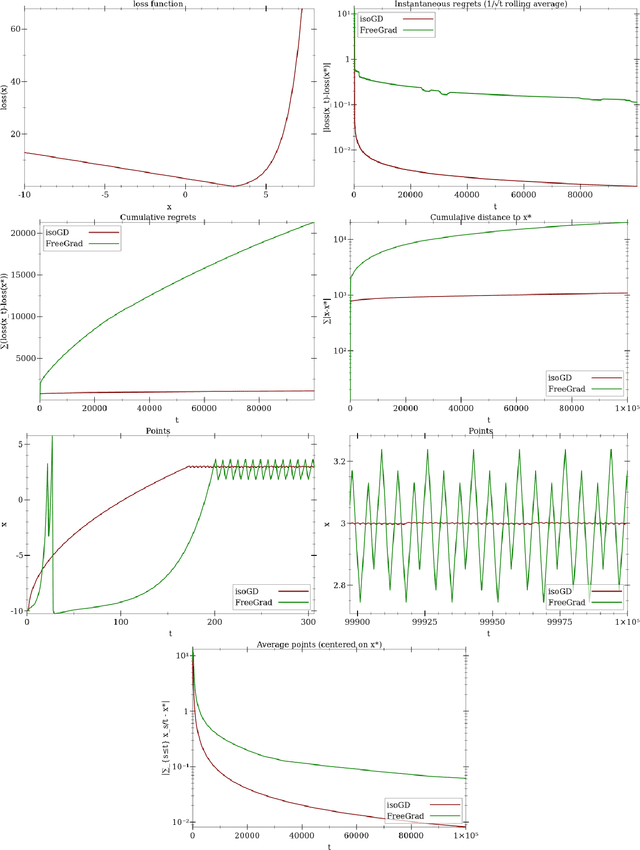
We extend and combine several tools of the literature to design fast, adaptive, anytime and scale-free online learning algorithms. Scale-free regret bounds must scale linearly with the maximum loss, both toward large losses and toward very small losses. Adaptive regret bounds demonstrate that an algorithm can take advantage of easy data and potentially have constant regret. We seek to develop fast algorithms that depend on as few parameters as possible, in particular they should be anytime and thus not depend on the time horizon. Our first and main tool, isotuning, is a generalization of the idea of balancing the trade-off of the regret. We develop a set of tools to design and analyze such learning rates easily and show that they adapts automatically to the rate of the regret (whether constant, $O(\log T)$, $O(\sqrt{T})$, etc.) within a factor 2 of the optimal learning rate in hindsight for the same observed quantities. The second tool is an online correction, which allows us to obtain centered bounds for many algorithms, to prevent the regret bounds from being vacuous when the domain is overly large or only partially constrained. The last tool, null updates, prevents the algorithm from performing overly large updates, which could result in unbounded regret, or even invalid updates. We develop a general theory using these tools and apply it to several standard algorithms. In particular, we (almost entirely) restore the adaptivity to small losses of FTRL for unbounded domains, design and prove scale-free adaptive guarantees for a variant of Mirror Descent (at least when the Bregman divergence is convex in its second argument), extend Adapt-ML-Prod to scale-free guarantees, and provide several other minor contributions about Prod, AdaHedge, BOA and Soft-Bayes.

Reducing Planning Complexity of General Reinforcement Learning with Non-Markovian Abstractions

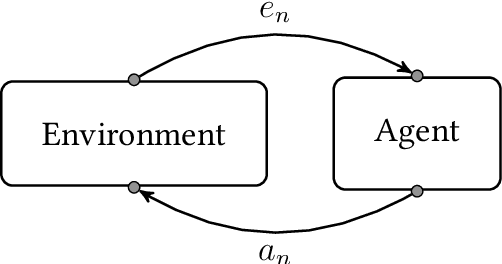
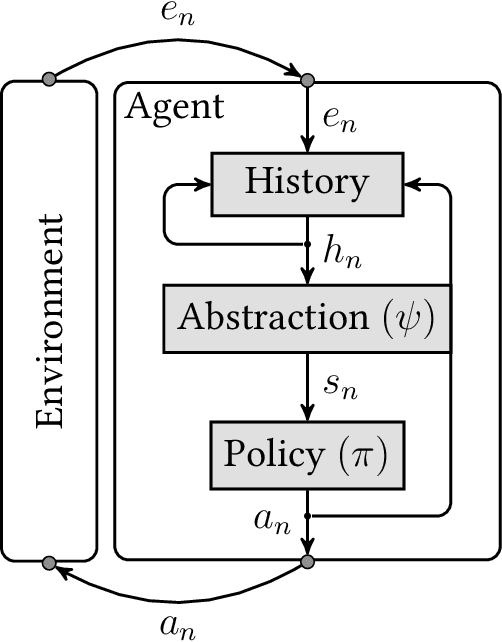
The field of General Reinforcement Learning (GRL) formulates the problem of sequential decision-making from ground up. The history of interaction constitutes a "ground" state of the system, which never repeats. On the one hand, this generality allows GRL to model almost every domain possible, e.g.\ Bandits, MDPs, POMDPs, PSRs, and history-based environments. On the other hand, in general, the near-optimal policies in GRL are functions of complete history, which hinders not only learning but also planning in GRL. The usual way around for the planning part is that the agent is given a Markovian abstraction of the underlying process. So, it can use any MDP planning algorithm to find a near-optimal policy. The Extreme State Aggregation (ESA) framework has extended this idea to non-Markovian abstractions without compromising on the possibility of planning through a (surrogate) MDP. A distinguishing feature of ESA is that it proves an upper bound of $O\left(\varepsilon^{-A} \cdot (1-\gamma)^{-2A}\right)$ on the number of states required for the surrogate MDP (where $A$ is the number of actions, $\gamma$ is the discount-factor, and $\varepsilon$ is the optimality-gap) which holds \emph{uniformly} for \emph{all} domains. While the possibility of a universal bound is quite remarkable, we show that this bound is very loose. We propose a novel non-MDP abstraction which allows for a much better upper bound of $O\left(\varepsilon^{-1} \cdot (1-\gamma)^{-2} \cdot A \cdot 2^{A}\right)$. Furthermore, we show that this bound can be improved further to $O\left(\varepsilon^{-1} \cdot (1-\gamma)^{-2} \cdot \log^3 A \right)$ by using an action-sequentialization method.