Malik Tiomoko
GIPSA-Lab, Grenoble-Alps University
LLMs as In-Context Meta-Learners for Model and Hyperparameter Selection
Oct 30, 2025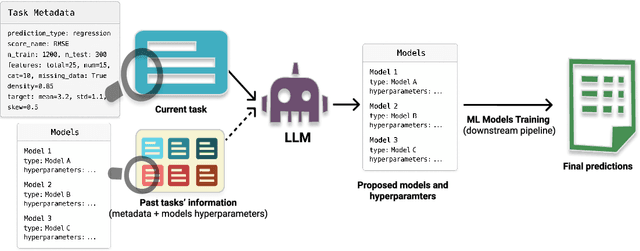
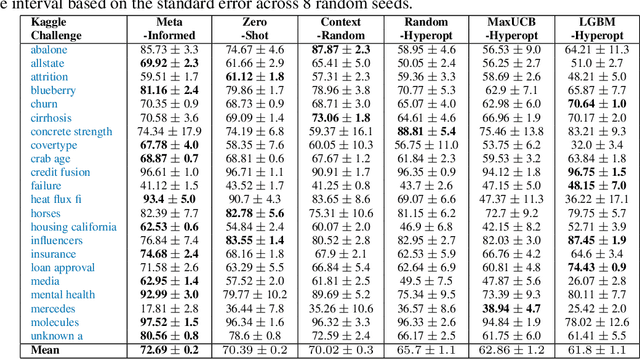
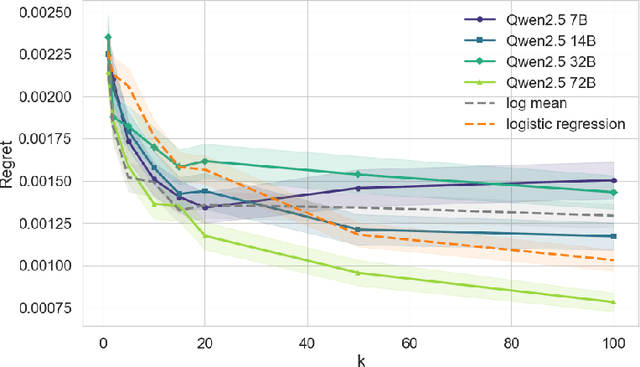
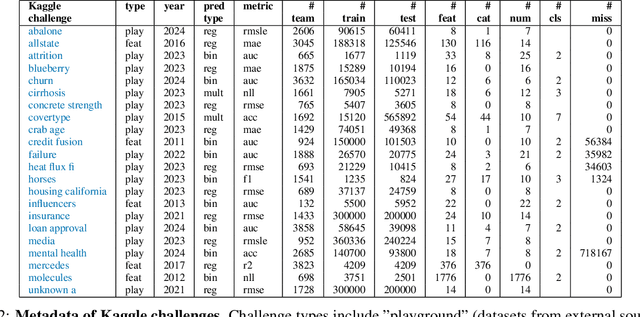
Abstract:Model and hyperparameter selection are critical but challenging in machine learning, typically requiring expert intuition or expensive automated search. We investigate whether large language models (LLMs) can act as in-context meta-learners for this task. By converting each dataset into interpretable metadata, we prompt an LLM to recommend both model families and hyperparameters. We study two prompting strategies: (1) a zero-shot mode relying solely on pretrained knowledge, and (2) a meta-informed mode augmented with examples of models and their performance on past tasks. Across synthetic and real-world benchmarks, we show that LLMs can exploit dataset metadata to recommend competitive models and hyperparameters without search, and that improvements from meta-informed prompting demonstrate their capacity for in-context meta-learning. These results highlight a promising new role for LLMs as lightweight, general-purpose assistants for model selection and hyperparameter optimization.
Incorporating priors in learning: a random matrix study under a teacher-student framework
Sep 26, 2025Abstract:Regularized linear regression is central to machine learning, yet its high-dimensional behavior with informative priors remains poorly understood. We provide the first exact asymptotic characterization of training and test risks for maximum a posteriori (MAP) regression with Gaussian priors centered at a domain-informed initialization. Our framework unifies ridge regression, least squares, and prior-informed estimators, and -- using random matrix theory -- yields closed-form risk formulas that expose the bias-variance-prior tradeoff, explain double descent, and quantify prior mismatch. We also identify a closed-form minimizer of test risk, enabling a simple estimator of the optimal regularization parameter. Simulations confirm the theory with high accuracy. By connecting Bayesian priors, classical regularization, and modern asymptotics, our results provide both conceptual clarity and practical guidance for learning with structured prior knowledge.
A Random Matrix Perspective of Echo State Networks: From Precise Bias--Variance Characterization to Optimal Regularization
Sep 26, 2025Abstract:We present a rigorous asymptotic analysis of Echo State Networks (ESNs) in a teacher student setting with a linear teacher with oracle weights. Leveraging random matrix theory, we derive closed form expressions for the asymptotic bias, variance, and mean-squared error (MSE) as functions of the input statistics, the oracle vector, and the ridge regularization parameter. The analysis reveals two key departures from classical ridge regression: (i) ESNs do not exhibit double descent, and (ii) ESNs attain lower MSE when both the number of training samples and the teacher memory length are limited. We further provide an explicit formula for the optimal regularization in the identity input covariance case, and propose an efficient numerical scheme to compute the optimum in the general case. Together, these results offer interpretable theory and practical guidelines for tuning ESNs, helping reconcile recent empirical observations with provable performance guarantees
Human in the Loop Adaptive Optimization for Improved Time Series Forecasting
May 21, 2025Abstract:Time series forecasting models often produce systematic, predictable errors even in critical domains such as energy, finance, and healthcare. We introduce a novel post training adaptive optimization framework that improves forecast accuracy without retraining or architectural changes. Our method automatically applies expressive transformations optimized via reinforcement learning, contextual bandits, or genetic algorithms to correct model outputs in a lightweight and model agnostic way. Theoretically, we prove that affine corrections always reduce the mean squared error; practically, we extend this idea with dynamic action based optimization. The framework also supports an optional human in the loop component: domain experts can guide corrections using natural language, which is parsed into actions by a language model. Across multiple benchmarks (e.g., electricity, weather, traffic), we observe consistent accuracy gains with minimal computational overhead. Our interactive demo shows the framework's real time usability. By combining automated post hoc refinement with interpretable and extensible mechanisms, our approach offers a powerful new direction for practical forecasting systems.
High-Dimensional Analysis of Bootstrap Ensemble Classifiers
May 20, 2025Abstract:Bootstrap methods have long been a cornerstone of ensemble learning in machine learning. This paper presents a theoretical analysis of bootstrap techniques applied to the Least Square Support Vector Machine (LSSVM) ensemble in the context of large and growing sample sizes and feature dimensionalities. Leveraging tools from Random Matrix Theory, we investigate the performance of this classifier that aggregates decision functions from multiple weak classifiers, each trained on different subsets of the data. We provide insights into the use of bootstrap methods in high-dimensional settings, enhancing our understanding of their impact. Based on these findings, we propose strategies to select the number of subsets and the regularization parameter that maximize the performance of the LSSVM. Empirical experiments on synthetic and real-world datasets validate our theoretical results.
Mantis: Lightweight Calibrated Foundation Model for User-Friendly Time Series Classification
Feb 21, 2025Abstract:In recent years, there has been increasing interest in developing foundation models for time series data that can generalize across diverse downstream tasks. While numerous forecasting-oriented foundation models have been introduced, there is a notable scarcity of models tailored for time series classification. To address this gap, we present Mantis, a new open-source foundation model for time series classification based on the Vision Transformer (ViT) architecture that has been pre-trained using a contrastive learning approach. Our experimental results show that Mantis outperforms existing foundation models both when the backbone is frozen and when fine-tuned, while achieving the lowest calibration error. In addition, we propose several adapters to handle the multivariate setting, reducing memory requirements and modeling channel interdependence.
Analysing Multi-Task Regression via Random Matrix Theory with Application to Time Series Forecasting
Jun 14, 2024



Abstract:In this paper, we introduce a novel theoretical framework for multi-task regression, applying random matrix theory to provide precise performance estimations, under high-dimensional, non-Gaussian data distributions. We formulate a multi-task optimization problem as a regularization technique to enable single-task models to leverage multi-task learning information. We derive a closed-form solution for multi-task optimization in the context of linear models. Our analysis provides valuable insights by linking the multi-task learning performance to various model statistics such as raw data covariances, signal-generating hyperplanes, noise levels, as well as the size and number of datasets. We finally propose a consistent estimation of training and testing errors, thereby offering a robust foundation for hyperparameter optimization in multi-task regression scenarios. Experimental validations on both synthetic and real-world datasets in regression and multivariate time series forecasting demonstrate improvements on univariate models, incorporating our method into the training loss and thus leveraging multivariate information.
Random matrix theory improved Fréchet mean of symmetric positive definite matrices
May 10, 2024



Abstract:In this study, we consider the realm of covariance matrices in machine learning, particularly focusing on computing Fr\'echet means on the manifold of symmetric positive definite matrices, commonly referred to as Karcher or geometric means. Such means are leveraged in numerous machine-learning tasks. Relying on advanced statistical tools, we introduce a random matrix theory-based method that estimates Fr\'echet means, which is particularly beneficial when dealing with low sample support and a high number of matrices to average. Our experimental evaluation, involving both synthetic and real-world EEG and hyperspectral datasets, shows that we largely outperform state-of-the-art methods.
Random Matrix Analysis to Balance between Supervised and Unsupervised Learning under the Low Density Separation Assumption
Oct 20, 2023



Abstract:We propose a theoretical framework to analyze semi-supervised classification under the low density separation assumption in a high-dimensional regime. In particular, we introduce QLDS, a linear classification model, where the low density separation assumption is implemented via quadratic margin maximization. The algorithm has an explicit solution with rich theoretical properties, and we show that particular cases of our algorithm are the least-square support vector machine in the supervised case, the spectral clustering in the fully unsupervised regime, and a class of semi-supervised graph-based approaches. As such, QLDS establishes a smooth bridge between these supervised and unsupervised learning methods. Using recent advances in the random matrix theory, we formally derive a theoretical evaluation of the classification error in the asymptotic regime. As an application, we derive a hyperparameter selection policy that finds the best balance between the supervised and the unsupervised terms of our learning criterion. Finally, we provide extensive illustrations of our framework, as well as an experimental study on several benchmarks to demonstrate that QLDS, while being computationally more efficient, improves over cross-validation for hyperparameter selection, indicating a high promise of the usage of random matrix theory for semi-supervised model selection.
PCA-based Multi Task Learning: a Random Matrix Approach
Nov 01, 2021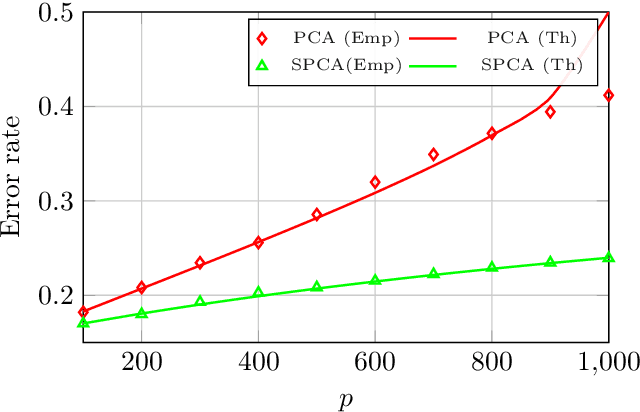

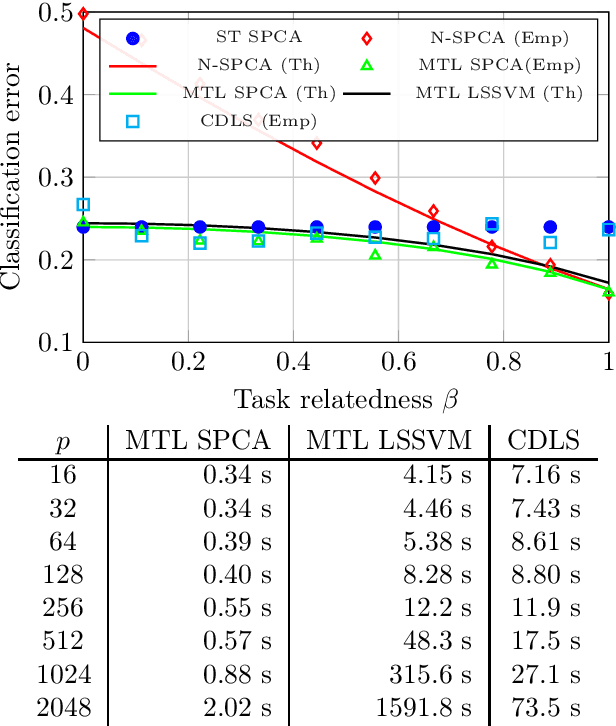
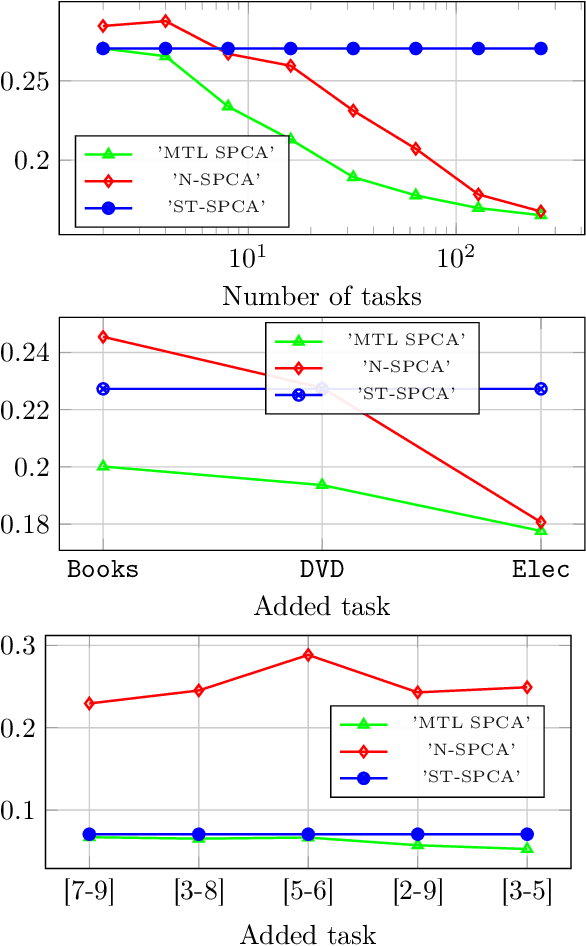
Abstract:The article proposes and theoretically analyses a \emph{computationally efficient} multi-task learning (MTL) extension of popular principal component analysis (PCA)-based supervised learning schemes \cite{barshan2011supervised,bair2006prediction}. The analysis reveals that (i) by default learning may dramatically fail by suffering from \emph{negative transfer}, but that (ii) simple counter-measures on data labels avert negative transfer and necessarily result in improved performances. Supporting experiments on synthetic and real data benchmarks show that the proposed method achieves comparable performance with state-of-the-art MTL methods but at a \emph{significantly reduced computational cost}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge