High-Dimensional Analysis of Bootstrap Ensemble Classifiers

Bootstrap methods have long been a cornerstone of ensemble learning in machine learning. This paper presents a theoretical analysis of bootstrap techniques applied to the Least Square Support Vector Machine (LSSVM) ensemble in the context of large and growing sample sizes and feature dimensionalities. Leveraging tools from Random Matrix Theory, we investigate the performance of this classifier that aggregates decision functions from multiple weak classifiers, each trained on different subsets of the data. We provide insights into the use of bootstrap methods in high-dimensional settings, enhancing our understanding of their impact. Based on these findings, we propose strategies to select the number of subsets and the regularization parameter that maximize the performance of the LSSVM. Empirical experiments on synthetic and real-world datasets validate our theoretical results.

Generalization Error Bounds for Iterative Recovery Algorithms Unfolded as Neural Networks

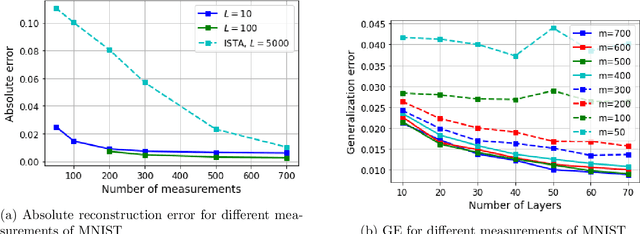
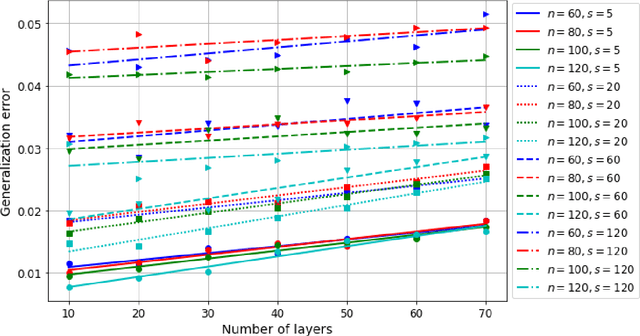
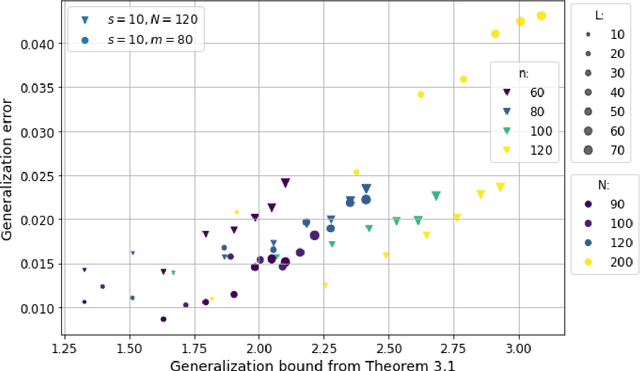
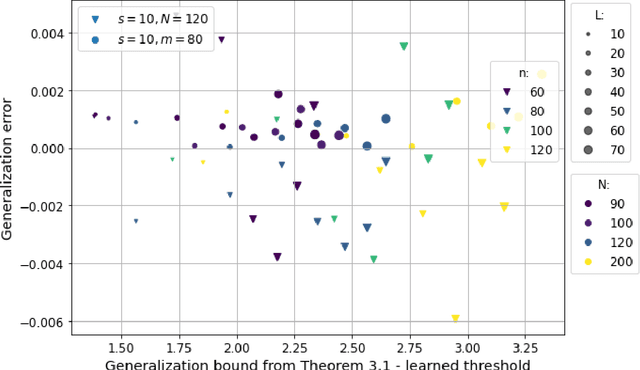
Motivated by the learned iterative soft thresholding algorithm (LISTA), we introduce a general class of neural networks suitable for sparse reconstruction from few linear measurements. By allowing a wide range of degrees of weight-sharing between the layers, we enable a unified analysis for very different neural network types, ranging from recurrent ones to networks more similar to standard feedforward neural networks. Based on training samples, via empirical risk minimization we aim at learning the optimal network parameters and thereby the optimal network that reconstructs signals from their low-dimensional linear measurements. We derive generalization bounds by analyzing the Rademacher complexity of hypothesis classes consisting of such deep networks, that also take into account the thresholding parameters. We obtain estimates of the sample complexity that essentially depend only linearly on the number of parameters and on the depth. We apply our main result to obtain specific generalization bounds for several practical examples, including different algorithms for (implicit) dictionary learning, and convolutional neural networks.

Generalization bounds for deep thresholding networks

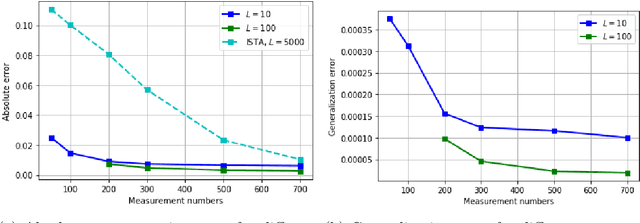
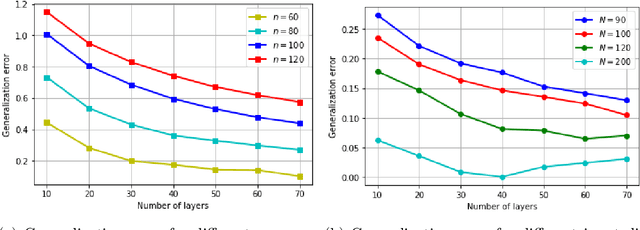
We consider compressive sensing in the scenario where the sparsity basis (dictionary) is not known in advance, but needs to be learned from examples. Motivated by the well-known iterative soft thresholding algorithm for the reconstruction, we define deep networks parametrized by the dictionary, which we call deep thresholding networks. Based on training samples, we aim at learning the optimal sparsifying dictionary and thereby the optimal network that reconstructs signals from their low-dimensional linear measurements. The dictionary learning is performed via minimizing the empirical risk. We derive generalization bounds by analyzing the Rademacher complexity of hypothesis classes consisting of such deep networks. We obtain estimates of the sample complexity that depend only linearly on the dimensions and on the depth.