Asymptotic Bayes risk of semi-supervised learning with uncertain labeling

This article considers a semi-supervised classification setting on a Gaussian mixture model, where the data is not labeled strictly as usual, but instead with uncertain labels. Our main aim is to compute the Bayes risk for this model. We compare the behavior of the Bayes risk and the best known algorithm for this model. This comparison eventually gives new insights over the algorithm.

A Large Dimensional Analysis of Multi-task Semi-Supervised Learning

This article conducts a large dimensional study of a simple yet quite versatile classification model, encompassing at once multi-task and semi-supervised learning, and taking into account uncertain labeling. Using tools from random matrix theory, we characterize the asymptotics of some key functionals, which allows us on the one hand to predict the performances of the algorithm, and on the other hand to reveal some counter-intuitive guidance on how to use it efficiently. The model, powerful enough to provide good performance guarantees, is also straightforward enough to provide strong insights into its behavior.

Asymptotic Gaussian Fluctuations of Eigenvectors in Spectral Clustering

The performance of spectral clustering relies on the fluctuations of the entries of the eigenvectors of a similarity matrix, which has been left uncharacterized until now. In this letter, it is shown that the signal $+$ noise structure of a general spike random matrix model is transferred to the eigenvectors of the corresponding Gram kernel matrix and the fluctuations of their entries are Gaussian in the large-dimensional regime. This CLT-like result was the last missing piece to precisely predict the classification performance of spectral clustering. The proposed proof is very general and relies solely on the rotational invariance of the noise. Numerical experiments on synthetic and real data illustrate the universality of this phenomenon.

A Random Matrix Approach to Low-Multilinear-Rank Tensor Approximation

This work presents a comprehensive understanding of the estimation of a planted low-rank signal from a general spiked tensor model near the computational threshold. Relying on standard tools from the theory of large random matrices, we characterize the large-dimensional spectral behavior of the unfoldings of the data tensor and exhibit relevant signal-to-noise ratios governing the detectability of the principal directions of the signal. These results allow to accurately predict the reconstruction performance of truncated multilinear SVD (MLSVD) in the non-trivial regime. This is particularly important since it serves as an initialization of the higher-order orthogonal iteration (HOOI) scheme, whose convergence to the best low-multilinear-rank approximation depends entirely on its initialization. We give a sufficient condition for the convergence of HOOI and show that the number of iterations before convergence tends to $1$ in the large-dimensional limit.

Asymptotic Bayes risk of semi-supervised multitask learning on Gaussian mixture

The article considers semi-supervised multitask learning on a Gaussian mixture model (GMM). Using methods from statistical physics, we compute the asymptotic Bayes risk of each task in the regime of large datasets in high dimension, from which we analyze the role of task similarity in learning and evaluate the performance gain when tasks are learned together rather than separately. In the supervised case, we derive a simple algorithm that attains the Bayes optimal performance.

When Random Tensors meet Random Matrices

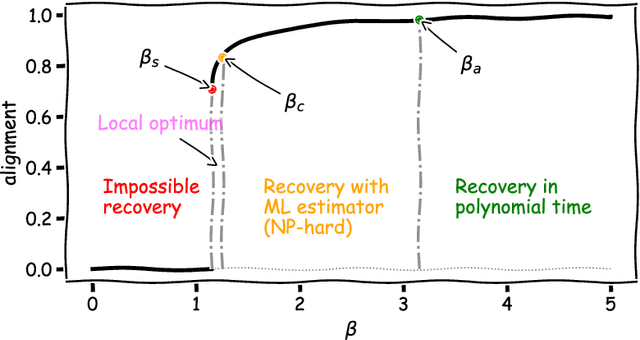
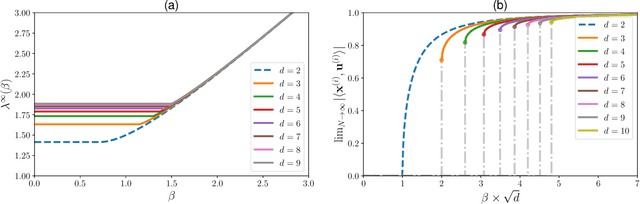
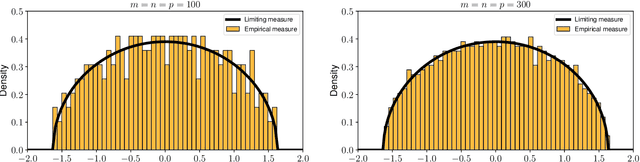
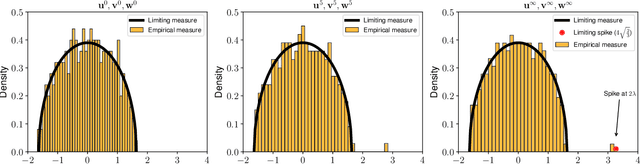
Relying on random matrix theory (RMT), this paper studies asymmetric order-$d$ spiked tensor models with Gaussian noise. Using the variational definition of the singular vectors and values of (Lim, 2005), we show that the analysis of the considered model boils down to the analysis of an equivalent spiked symmetric block-wise random matrix, that is constructed from contractions of the studied tensor with the singular vectors associated to its best rank-1 approximation. Our approach allows the exact characterization of the almost sure asymptotic singular value and alignments of the corresponding singular vectors with the true spike components, when $\frac{n_i}{\sum_{j=1}^d n_j}\to c_i\in [0, 1]$ with $n_i$'s the tensor dimensions. In contrast to other works that rely mostly on tools from statistical physics to study random tensors, our results rely solely on classical RMT tools such as Stein's lemma. Finally, classical RMT results concerning spiked random matrices are recovered as a particular case.

PCA-based Multi Task Learning: a Random Matrix Approach

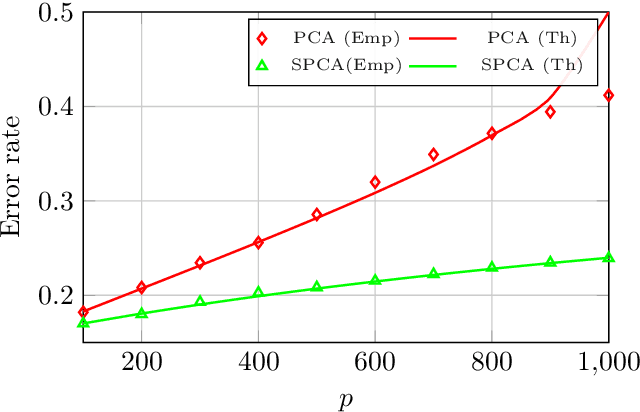
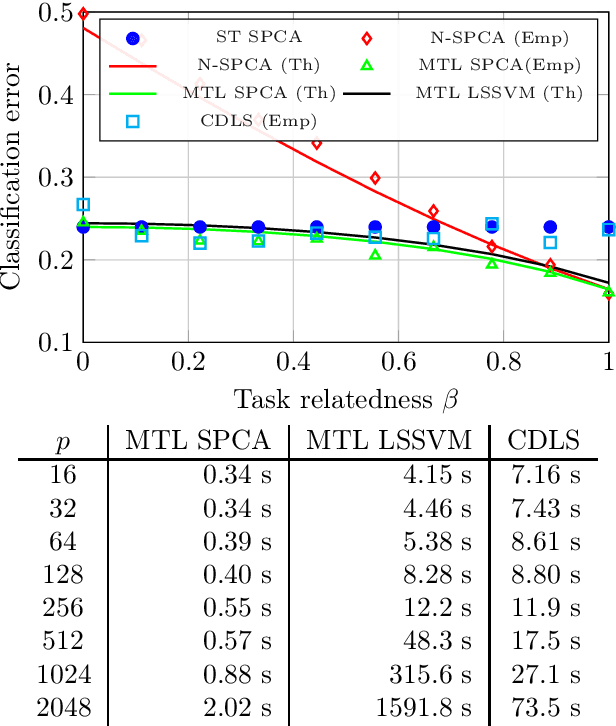
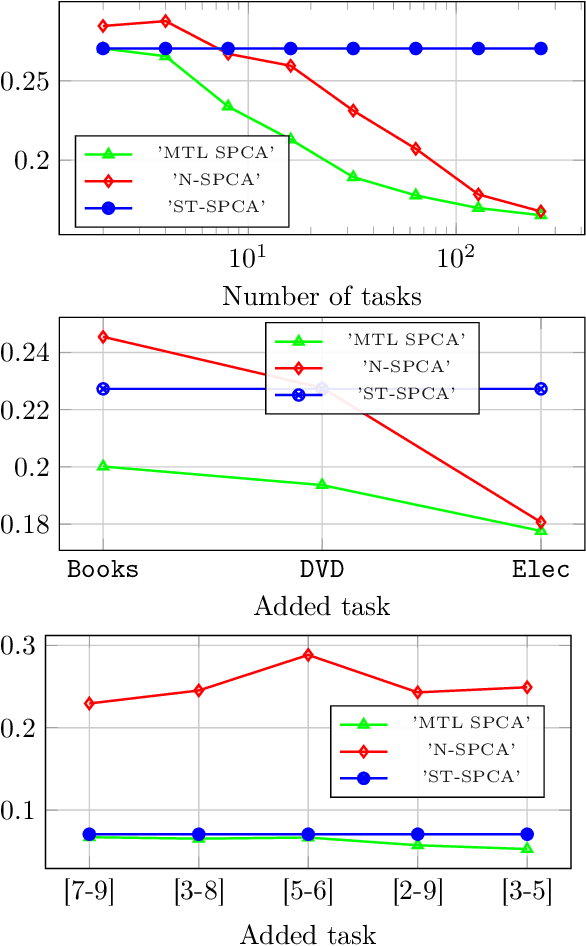
The article proposes and theoretically analyses a \emph{computationally efficient} multi-task learning (MTL) extension of popular principal component analysis (PCA)-based supervised learning schemes \cite{barshan2011supervised,bair2006prediction}. The analysis reveals that (i) by default learning may dramatically fail by suffering from \emph{negative transfer}, but that (ii) simple counter-measures on data labels avert negative transfer and necessarily result in improved performances. Supporting experiments on synthetic and real data benchmarks show that the proposed method achieves comparable performance with state-of-the-art MTL methods but at a \emph{significantly reduced computational cost}.

Multi-task learning on the edge: cost-efficiency and theoretical optimality

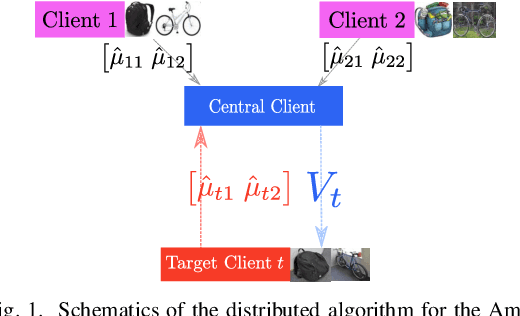
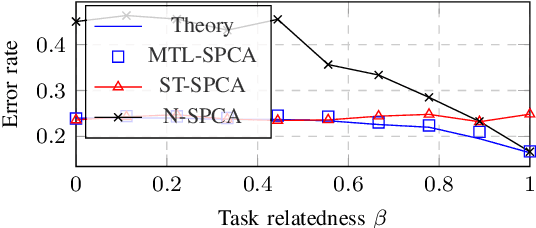
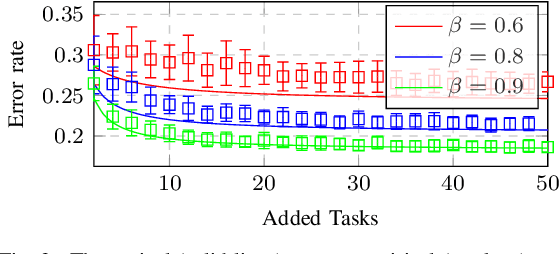
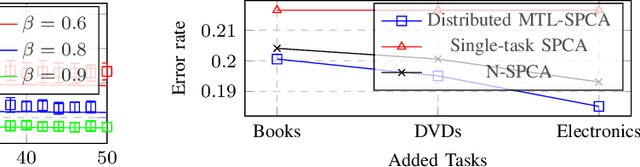
This article proposes a distributed multi-task learning (MTL) algorithm based on supervised principal component analysis (SPCA) which is: (i) theoretically optimal for Gaussian mixtures, (ii) computationally cheap and scalable. Supporting experiments on synthetic and real benchmark data demonstrate that significant energy gains can be obtained with no performance loss.

Random matrices in service of ML footprint: ternary random features with no performance loss

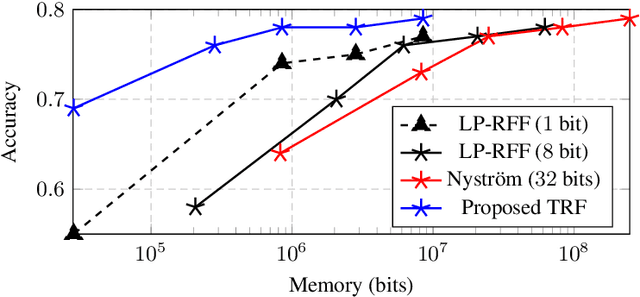
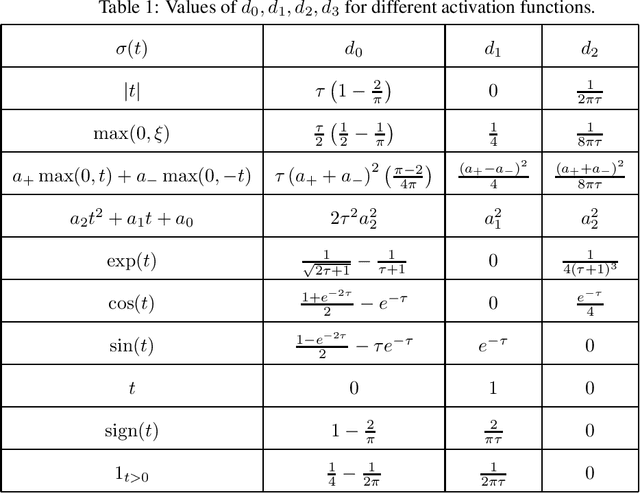
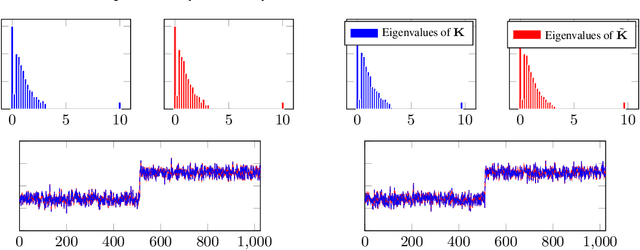
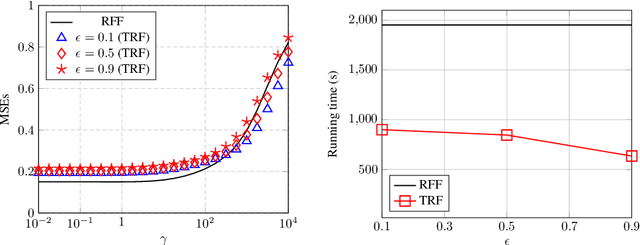
In this article, we investigate the spectral behavior of random features kernel matrices of the type ${\bf K} = \mathbb{E}_{{\bf w}} \left[\sigma\left({\bf w}^{\sf T}{\bf x}_i\right)\sigma\left({\bf w}^{\sf T}{\bf x}_j\right)\right]_{i,j=1}^n$, with nonlinear function $\sigma(\cdot)$, data ${\bf x}_1, \ldots, {\bf x}_n \in \mathbb{R}^p$, and random projection vector ${\bf w} \in \mathbb{R}^p$ having i.i.d. entries. In a high-dimensional setting where the number of data $n$ and their dimension $p$ are both large and comparable, we show, under a Gaussian mixture model for the data, that the eigenspectrum of ${\bf K}$ is independent of the distribution of the i.i.d.(zero-mean and unit-variance) entries of ${\bf w}$, and only depends on $\sigma(\cdot)$ via its (generalized) Gaussian moments $\mathbb{E}_{z\sim \mathcal N(0,1)}[\sigma'(z)]$ and $\mathbb{E}_{z\sim \mathcal N(0,1)}[\sigma''(z)]$. As a result, for any kernel matrix ${\bf K}$ of the form above, we propose a novel random features technique, called Ternary Random Feature (TRF), that (i) asymptotically yields the same limiting kernel as the original ${\bf K}$ in a spectral sense and (ii) can be computed and stored much more efficiently, by wisely tuning (in a data-dependent manner) the function $\sigma$ and the random vector ${\bf w}$, both taking values in $\{-1,0,1\}$. The computation of the proposed random features requires no multiplication, and a factor of $b$ times less bits for storage compared to classical random features such as random Fourier features, with $b$ the number of bits to store full precision values. Besides, it appears in our experiments on real data that the substantial gains in computation and storage are accompanied with somewhat improved performances compared to state-of-the-art random features compression/quantization methods.

Spectral properties of sample covariance matrices arising from random matrices with independent non identically distributed columns

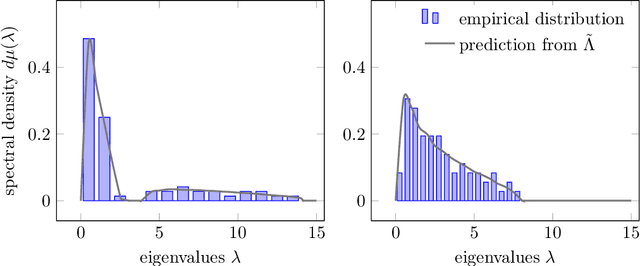
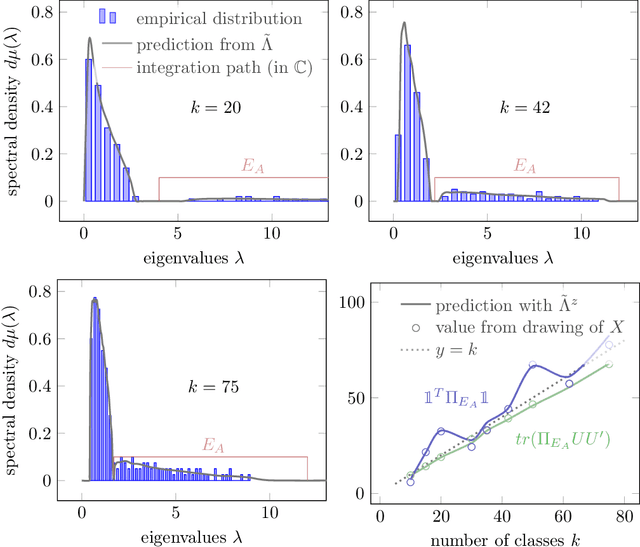
Given a random matrix $X= (x_1,\ldots, x_n)\in \mathcal M_{p,n}$ with independent columns and satisfying concentration of measure hypotheses and a parameter $z$ whose distance to the spectrum of $\frac{1}{n} XX^T$ should not depend on $p,n$, it was previously shown that the functionals $\text{tr}(AR(z))$, for $R(z) = (\frac{1}{n}XX^T- zI_p)^{-1}$ and $A\in \mathcal M_{p}$ deterministic, have a standard deviation of order $O(\|A\|_* / \sqrt n)$. Here, we show that $\|\mathbb E[R(z)] - \tilde R(z)\|_F \leq O(1/\sqrt n)$, where $\tilde R(z)$ is a deterministic matrix depending only on $z$ and on the means and covariances of the column vectors $x_1,\ldots, x_n$ (that do not have to be identically distributed). This estimation is key to providing accurate fluctuation rates of functionals of $X$ of interest (mostly related to its spectral properties) and is proved thanks to the introduction of a semi-metric $d_s$ defined on the set $\mathcal D_n(\mathbb H)$ of diagonal matrices with complex entries and positive imaginary part and satisfying, for all $D,D' \in \mathcal D_n(\mathbb H)$: $d_s(D,D') = \max_{i\in[n]} |D_i - D_i'|/ (\Im(D_i) \Im(D_i'))^{1/2}$. Possibly most importantly, the underlying concentration of measure assumption on the columns of $X$ finds an extremely natural ground for application in modern statistical machine learning algorithms where non-linear Lipschitz mappings and high number of classes form the base ingredients.