Joint System and Algorithm Design for Computationally Efficient Fan Beam Coded Aperture X-ray Coherent Scatter Imaging

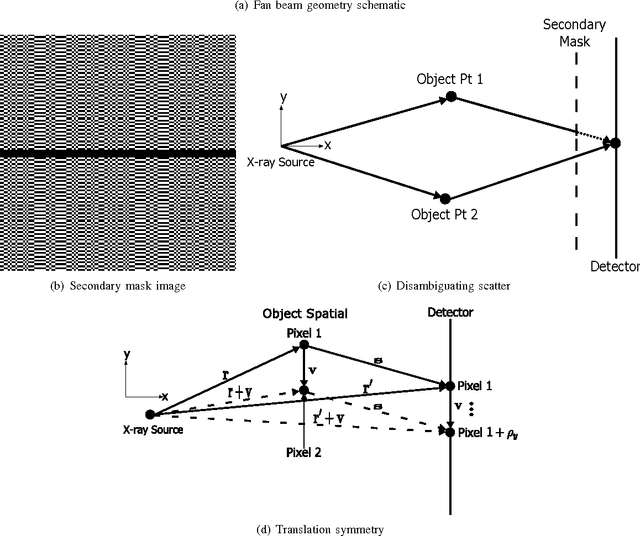
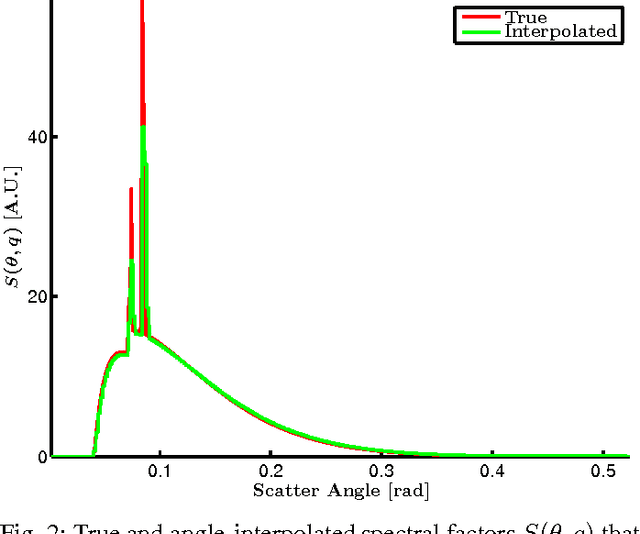
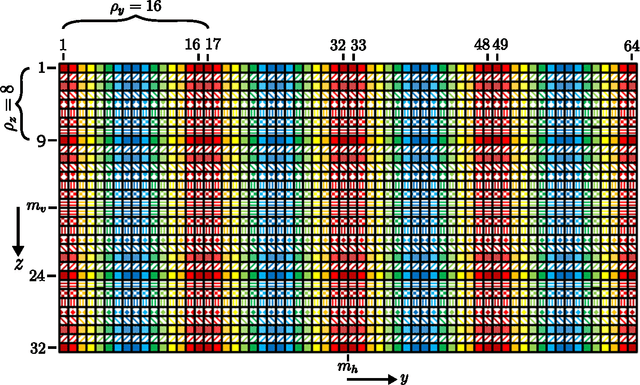
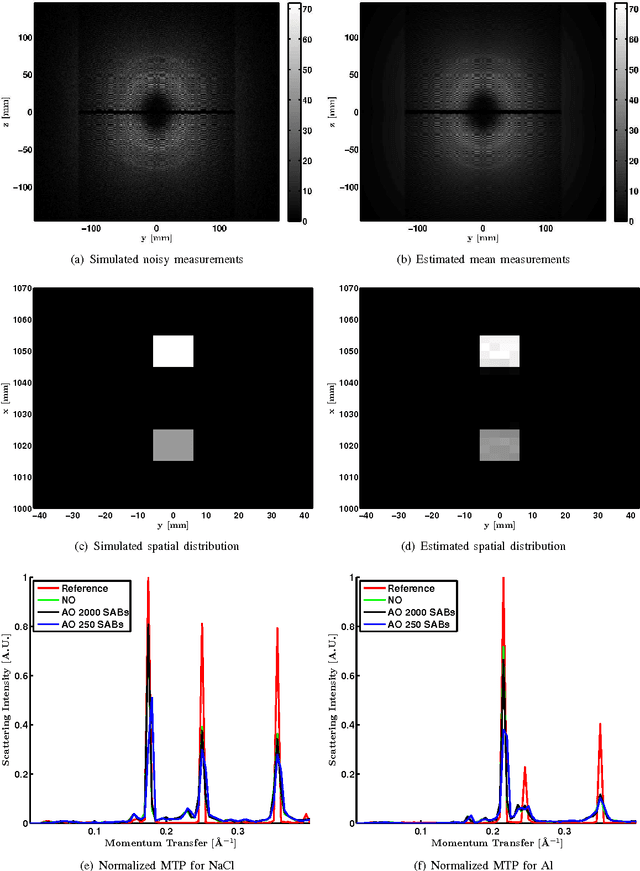
In x-ray coherent scatter tomography, tomographic measurements of the forward scatter distribution are used to infer scatter densities within a volume. A radiopaque 2D pattern placed between the object and the detector array enables the disambiguation between different scatter events. The use of a fan beam source illumination to speed up data acquisition relative to a pencil beam presents computational challenges. To facilitate the use of iterative algorithms based on a penalized Poisson log-likelihood function, efficient computational implementation of the forward and backward models are needed. Our proposed implementation exploits physical symmetries and structural properties of the system and suggests a joint system-algorithm design, where the system design choices are influenced by computational considerations, and in turn lead to reduced reconstruction time. Computational-time speedups of approximately 146 and 32 are achieved in the computation of the forward and backward models, respectively. Results validating the forward model and reconstruction algorithm are presented on simulated analytic and Monte Carlo data.

Preconditioned Stochastic Gradient Langevin Dynamics for Deep Neural Networks

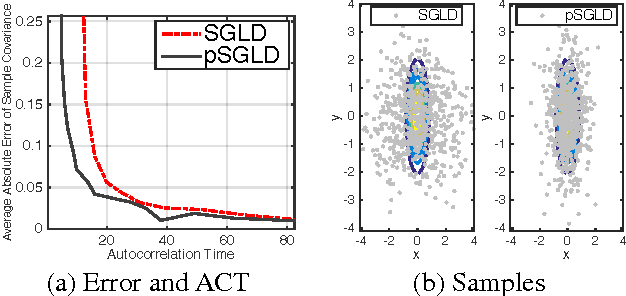
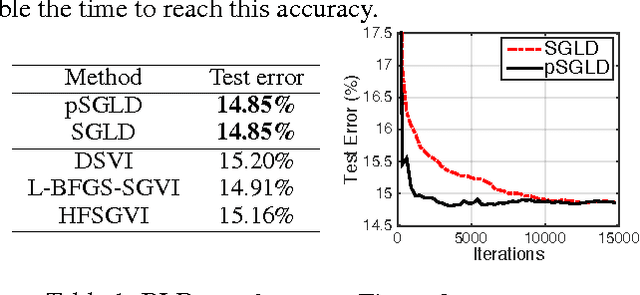
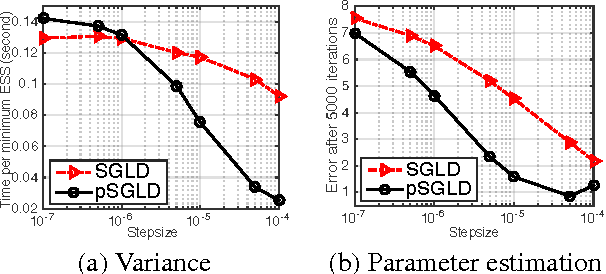
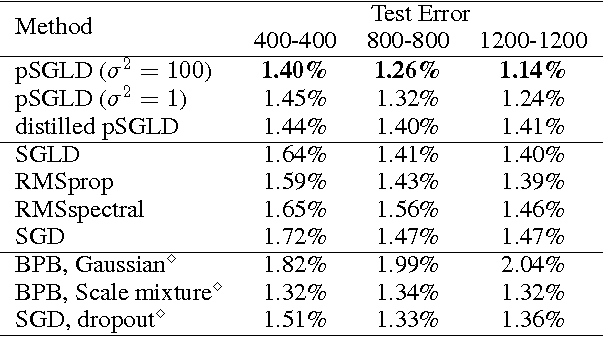
Effective training of deep neural networks suffers from two main issues. The first is that the parameter spaces of these models exhibit pathological curvature. Recent methods address this problem by using adaptive preconditioning for Stochastic Gradient Descent (SGD). These methods improve convergence by adapting to the local geometry of parameter space. A second issue is overfitting, which is typically addressed by early stopping. However, recent work has demonstrated that Bayesian model averaging mitigates this problem. The posterior can be sampled by using Stochastic Gradient Langevin Dynamics (SGLD). However, the rapidly changing curvature renders default SGLD methods inefficient. Here, we propose combining adaptive preconditioners with SGLD. In support of this idea, we give theoretical properties on asymptotic convergence and predictive risk. We also provide empirical results for Logistic Regression, Feedforward Neural Nets, and Convolutional Neural Nets, demonstrating that our preconditioned SGLD method gives state-of-the-art performance on these models.

High-Order Stochastic Gradient Thermostats for Bayesian Learning of Deep Models

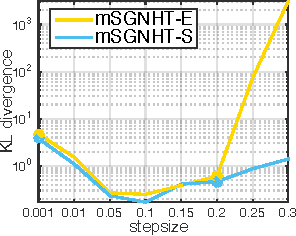
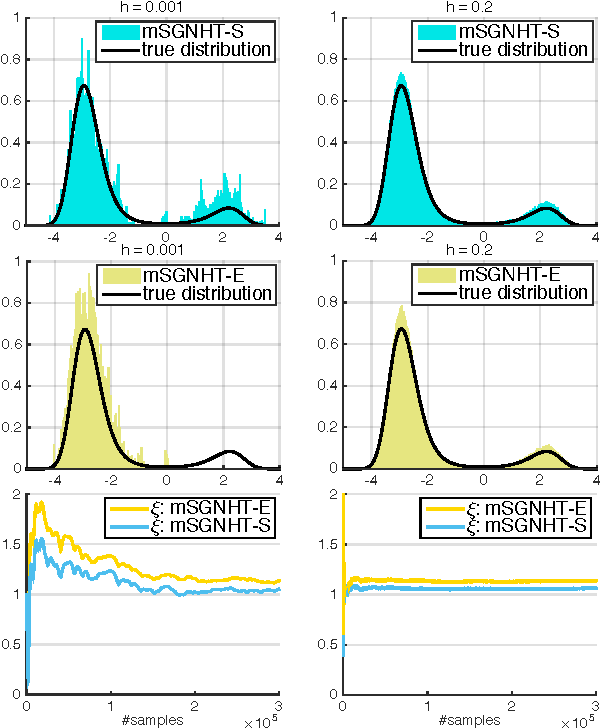
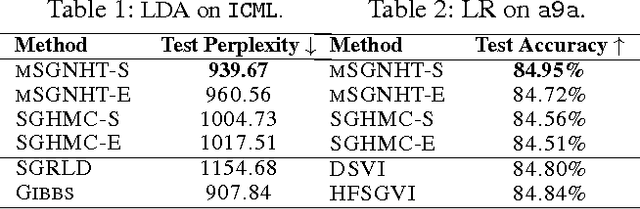
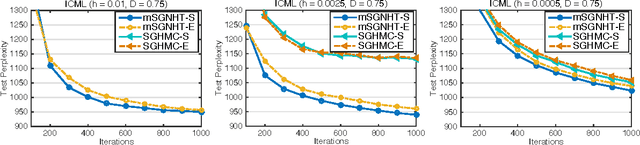
Learning in deep models using Bayesian methods has generated significant attention recently. This is largely because of the feasibility of modern Bayesian methods to yield scalable learning and inference, while maintaining a measure of uncertainty in the model parameters. Stochastic gradient MCMC algorithms (SG-MCMC) are a family of diffusion-based sampling methods for large-scale Bayesian learning. In SG-MCMC, multivariate stochastic gradient thermostats (mSGNHT) augment each parameter of interest, with a momentum and a thermostat variable to maintain stationary distributions as target posterior distributions. As the number of variables in a continuous-time diffusion increases, its numerical approximation error becomes a practical bottleneck, so better use of a numerical integrator is desirable. To this end, we propose use of an efficient symmetric splitting integrator in mSGNHT, instead of the traditional Euler integrator. We demonstrate that the proposed scheme is more accurate, robust, and converges faster. These properties are demonstrated to be desirable in Bayesian deep learning. Extensive experiments on two canonical models and their deep extensions demonstrate that the proposed scheme improves general Bayesian posterior sampling, particularly for deep models.

A Deep Generative Deconvolutional Image Model

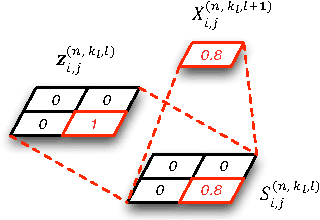
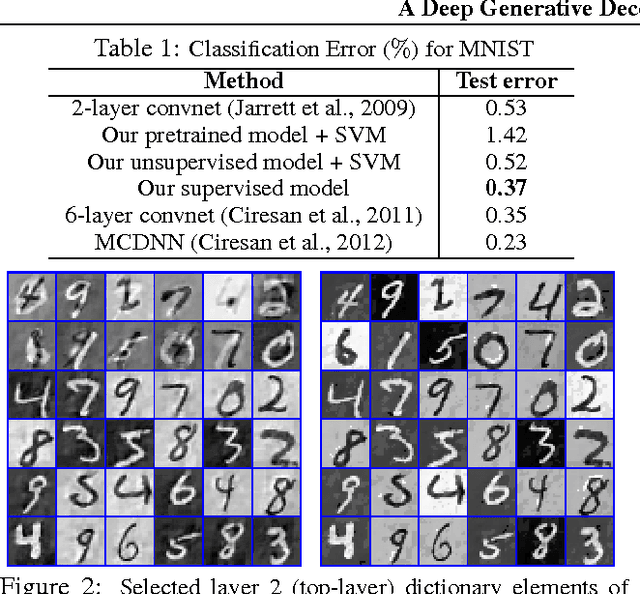
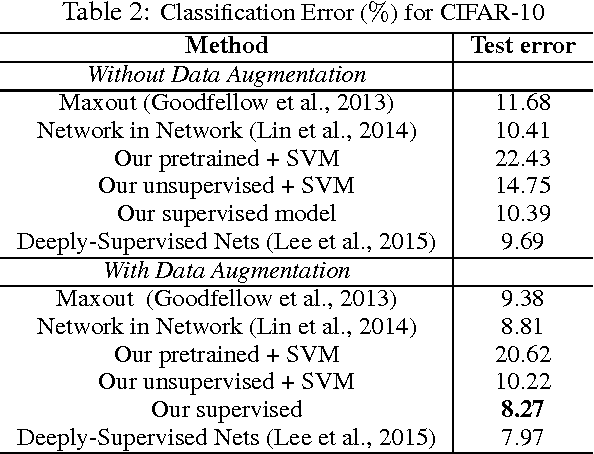
A deep generative model is developed for representation and analysis of images, based on a hierarchical convolutional dictionary-learning framework. Stochastic {\em unpooling} is employed to link consecutive layers in the model, yielding top-down image generation. A Bayesian support vector machine is linked to the top-layer features, yielding max-margin discrimination. Deep deconvolutional inference is employed when testing, to infer the latent features, and the top-layer features are connected with the max-margin classifier for discrimination tasks. The model is efficiently trained using a Monte Carlo expectation-maximization (MCEM) algorithm, with implementation on graphical processor units (GPUs) for efficient large-scale learning, and fast testing. Excellent results are obtained on several benchmark datasets, including ImageNet, demonstrating that the proposed model achieves results that are highly competitive with similarly sized convolutional neural networks.

Learning a Hybrid Architecture for Sequence Regression and Annotation

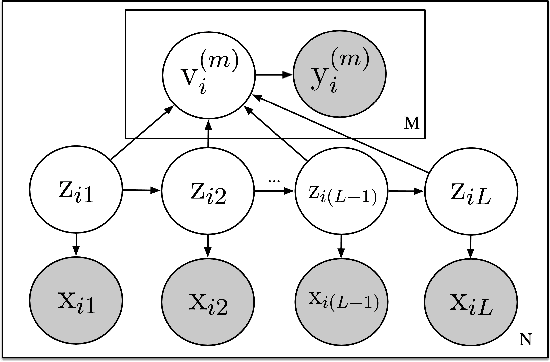
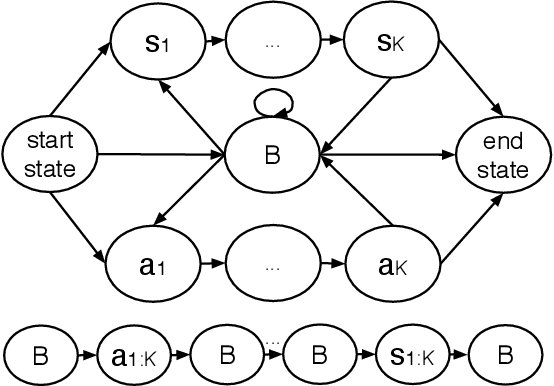
When learning a hidden Markov model (HMM), sequen- tial observations can often be complemented by real-valued summary response variables generated from the path of hid- den states. Such settings arise in numerous domains, includ- ing many applications in biology, like motif discovery and genome annotation. In this paper, we present a flexible frame- work for jointly modeling both latent sequence features and the functional mapping that relates the summary response variables to the hidden state sequence. The algorithm is com- patible with a rich set of mapping functions. Results show that the availability of additional continuous response vari- ables can simultaneously improve the annotation of the se- quential observations and yield good prediction performance in both synthetic data and real-world datasets.

Stick-Breaking Policy Learning in Dec-POMDPs

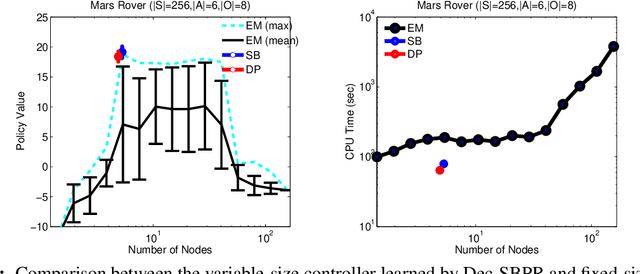
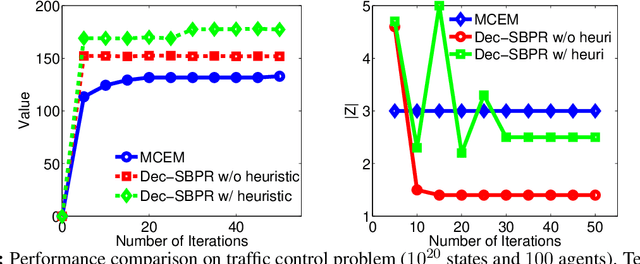
Expectation maximization (EM) has recently been shown to be an efficient algorithm for learning finite-state controllers (FSCs) in large decentralized POMDPs (Dec-POMDPs). However, current methods use fixed-size FSCs and often converge to maxima that are far from optimal. This paper considers a variable-size FSC to represent the local policy of each agent. These variable-size FSCs are constructed using a stick-breaking prior, leading to a new framework called \emph{decentralized stick-breaking policy representation} (Dec-SBPR). This approach learns the controller parameters with a variational Bayesian algorithm without having to assume that the Dec-POMDP model is available. The performance of Dec-SBPR is demonstrated on several benchmark problems, showing that the algorithm scales to large problems while outperforming other state-of-the-art methods.

Deep Temporal Sigmoid Belief Networks for Sequence Modeling

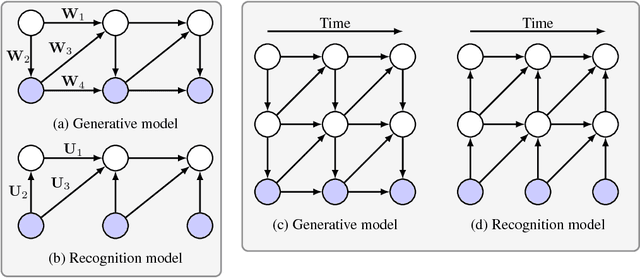
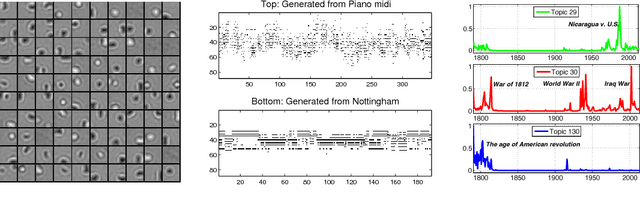
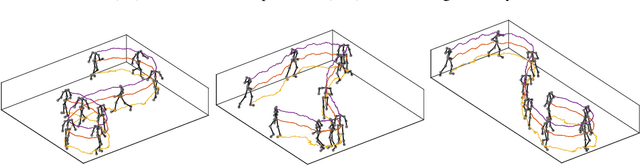
Deep dynamic generative models are developed to learn sequential dependencies in time-series data. The multi-layered model is designed by constructing a hierarchy of temporal sigmoid belief networks (TSBNs), defined as a sequential stack of sigmoid belief networks (SBNs). Each SBN has a contextual hidden state, inherited from the previous SBNs in the sequence, and is used to regulate its hidden bias. Scalable learning and inference algorithms are derived by introducing a recognition model that yields fast sampling from the variational posterior. This recognition model is trained jointly with the generative model, by maximizing its variational lower bound on the log-likelihood. Experimental results on bouncing balls, polyphonic music, motion capture, and text streams show that the proposed approach achieves state-of-the-art predictive performance, and has the capacity to synthesize various sequences.

Scalable Bayesian Non-Negative Tensor Factorization for Massive Count Data

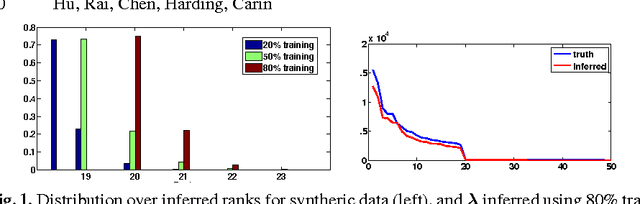
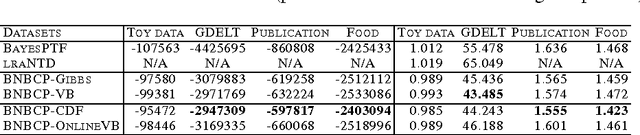
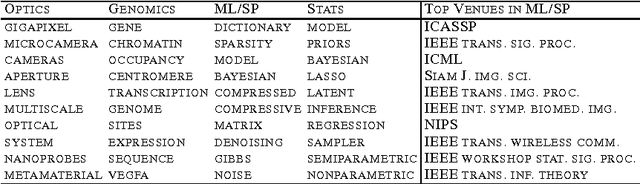
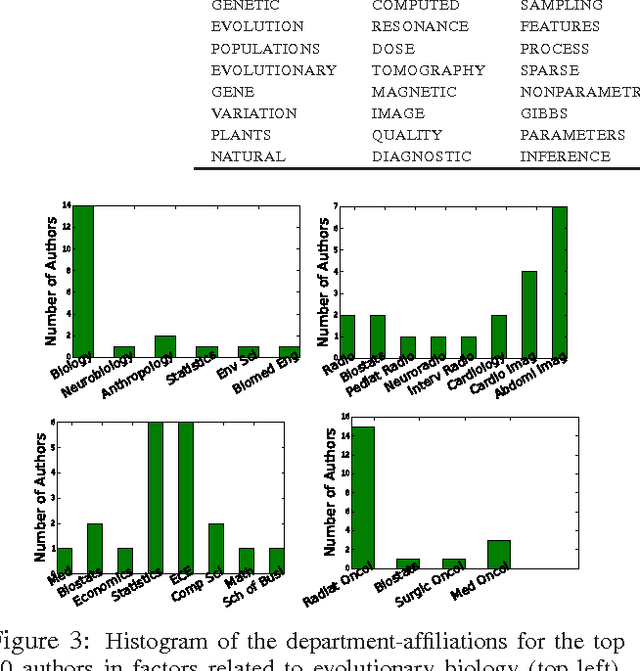
We present a Bayesian non-negative tensor factorization model for count-valued tensor data, and develop scalable inference algorithms (both batch and online) for dealing with massive tensors. Our generative model can handle overdispersed counts as well as infer the rank of the decomposition. Moreover, leveraging a reparameterization of the Poisson distribution as a multinomial facilitates conjugacy in the model and enables simple and efficient Gibbs sampling and variational Bayes (VB) inference updates, with a computational cost that only depends on the number of nonzeros in the tensor. The model also provides a nice interpretability for the factors; in our model, each factor corresponds to a "topic". We develop a set of online inference algorithms that allow further scaling up the model to massive tensors, for which batch inference methods may be infeasible. We apply our framework on diverse real-world applications, such as \emph{multiway} topic modeling on a scientific publications database, analyzing a political science data set, and analyzing a massive household transactions data set.

Zero-Truncated Poisson Tensor Factorization for Massive Binary Tensors

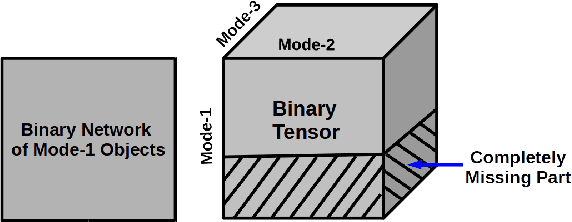
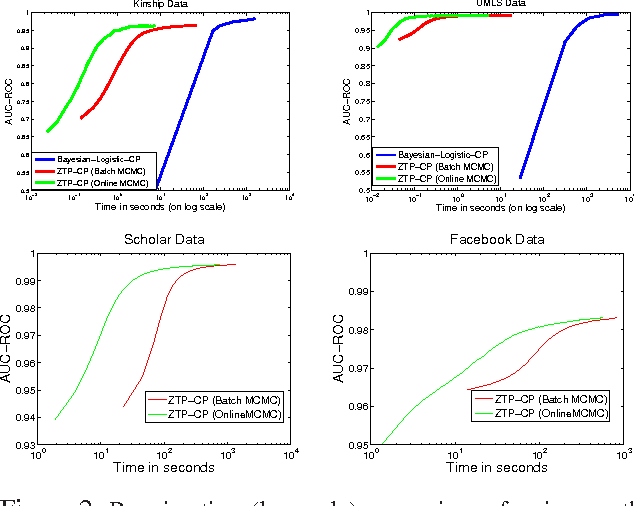
We present a scalable Bayesian model for low-rank factorization of massive tensors with binary observations. The proposed model has the following key properties: (1) in contrast to the models based on the logistic or probit likelihood, using a zero-truncated Poisson likelihood for binary data allows our model to scale up in the number of \emph{ones} in the tensor, which is especially appealing for massive but sparse binary tensors; (2) side-information in form of binary pairwise relationships (e.g., an adjacency network) between objects in any tensor mode can also be leveraged, which can be especially useful in "cold-start" settings; and (3) the model admits simple Bayesian inference via batch, as well as \emph{online} MCMC; the latter allows scaling up even for \emph{dense} binary data (i.e., when the number of ones in the tensor/network is also massive). In addition, non-negative factor matrices in our model provide easy interpretability, and the tensor rank can be inferred from the data. We evaluate our model on several large-scale real-world binary tensors, achieving excellent computational scalability, and also demonstrate its usefulness in leveraging side-information provided in form of mode-network(s).

Alternating Minimization Algorithm with Automatic Relevance Determination for Transmission Tomography under Poisson Noise

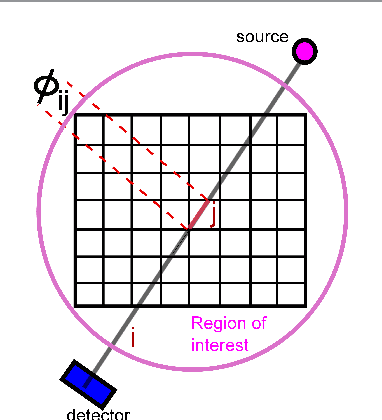
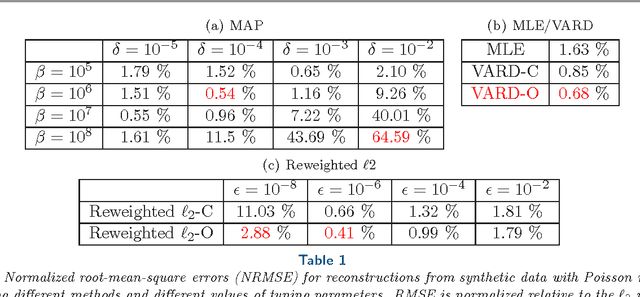
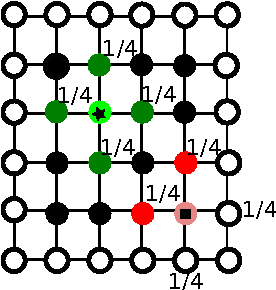
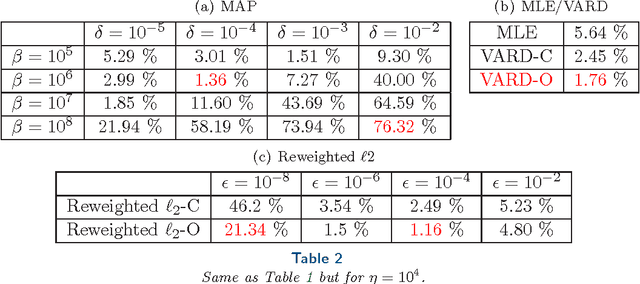
We propose a globally convergent alternating minimization (AM) algorithm for image reconstruction in transmission tomography, which extends automatic relevance determination (ARD) to Poisson noise models with Beer's law. The algorithm promotes solutions that are sparse in the pixel/voxel-differences domain by introducing additional latent variables, one for each pixel/voxel, and then learning these variables from the data using a hierarchical Bayesian model. Importantly, the proposed AM algorithm is free of any tuning parameters with image quality comparable to standard penalized likelihood methods. Our algorithm exploits optimization transfer principles which reduce the problem into parallel 1D optimization tasks (one for each pixel/voxel), making the algorithm feasible for large-scale problems. This approach considerably reduces the computational bottleneck of ARD associated with the posterior variances. Positivity constraints inherent in transmission tomography problems are also enforced. We demonstrate the performance of the proposed algorithm for x-ray computed tomography using synthetic and real-world datasets. The algorithm is shown to have much better performance than prior ARD algorithms based on approximate Gaussian noise models, even for high photon flux.