Adaptive posterior distributions for uncertainty analysis of covariance matrices in Bayesian inversion problems for multioutput signals

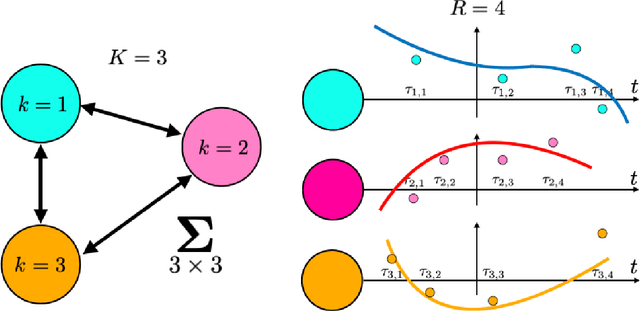
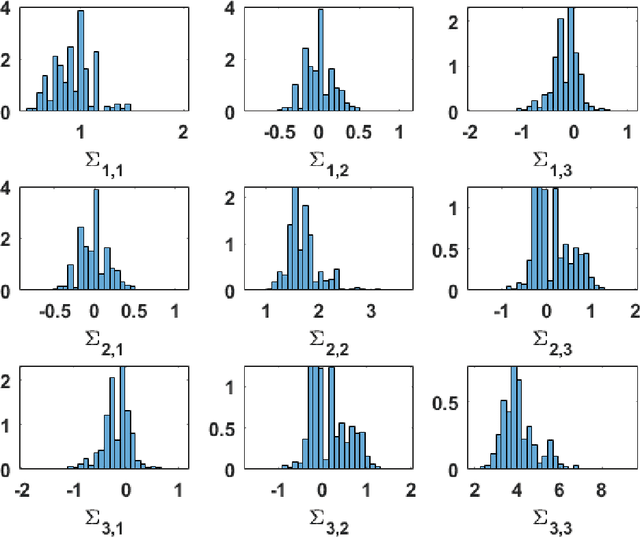
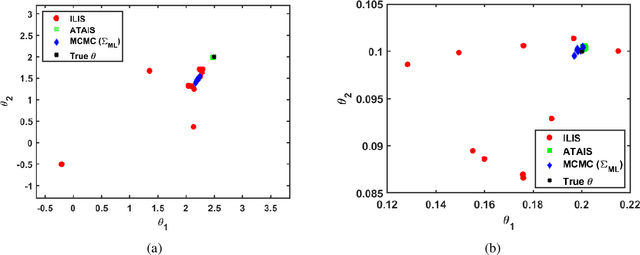
In this paper we address the problem of performing Bayesian inference for the parameters of a nonlinear multi-output model and the covariance matrix of the different output signals. We propose an adaptive importance sampling (AIS) scheme for multivariate Bayesian inversion problems, which is based in two main ideas: the variables of interest are split in two blocks and the inference takes advantage of known analytical optimization formulas. We estimate both the unknown parameters of the multivariate non-linear model and the covariance matrix of the noise. In the first part of the proposed inference scheme, a novel AIS technique called adaptive target adaptive importance sampling (ATAIS) is designed, which alternates iteratively between an IS technique over the parameters of the non-linear model and a frequentist approach for the covariance matrix of the noise. In the second part of the proposed inference scheme, a prior density over the covariance matrix is considered and the cloud of samples obtained by ATAIS are recycled and re-weighted to obtain a complete Bayesian study over the model parameters and covariance matrix. ATAIS is the main contribution of the work. Additionally, the inverted layered importance sampling (ILIS) is presented as a possible compelling algorithm (but based on a conceptually simpler idea). Different numerical examples show the benefits of the proposed approaches

Universal and Automatic Elbow Detection for Learning the Effective Number of Components in Model Selection Problems

We design a Universal Automatic Elbow Detector (UAED) for deciding the effective number of components in model selection problems. The relationship with the information criteria widely employed in the literature is also discussed. The proposed UAED does not require the knowledge of a likelihood function and can be easily applied in diverse applications, such as regression and classification, feature and/or order selection, clustering, and dimension reduction. Several experiments involving synthetic and real data show the advantages of the proposed scheme with benchmark techniques in the literature.

Spectral information criterion for automatic elbow detection

We introduce a generalized information criterion that contains other well-known information criteria, such as Bayesian information Criterion (BIC) and Akaike information criterion (AIC), as special cases. Furthermore, the proposed spectral information criterion (SIC) is also more general than the other information criteria, e.g., since the knowledge of a likelihood function is not strictly required. SIC extracts geometric features of the error curve and, as a consequence, it can be considered an automatic elbow detector. SIC provides a subset of all possible models, with a cardinality that often is much smaller than the total number of possible models. The elements of this subset are elbows of the error curve. A practical rule for selecting a unique model within the sets of elbows is suggested as well. Theoretical invariance properties of SIC are analyzed. Moreover, we test SIC in ideal scenarios where provides always the optimal expected results. We also test SIC in several numerical experiments: some involving synthetic data, and two experiments involving real datasets. They are all real-world applications such as clustering, variable selection, or polynomial order selection, to name a few. The results show the benefits of the proposed scheme. Matlab code related to the experiments is also provided. Possible future research lines are finally discussed.

An exhaustive variable selection study for linear models of soundscape emotions: rankings and Gibbs analysis

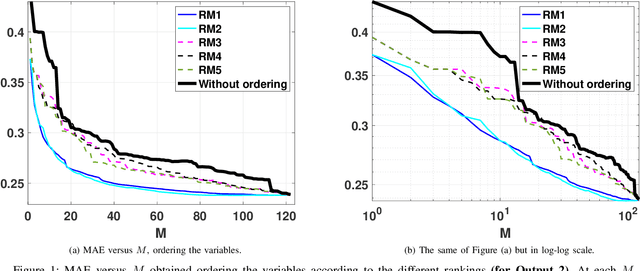
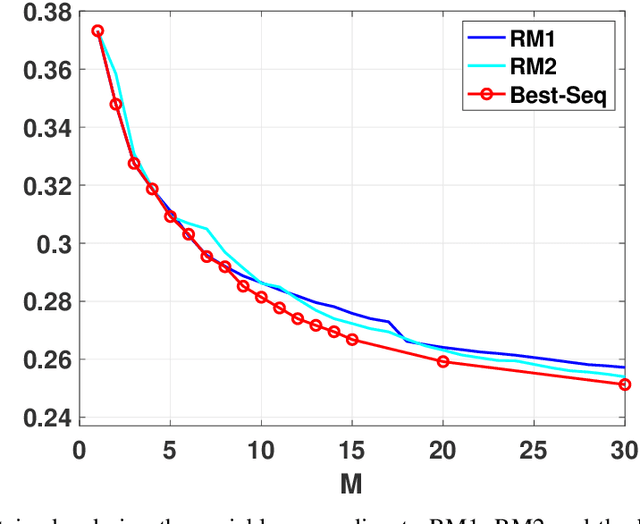
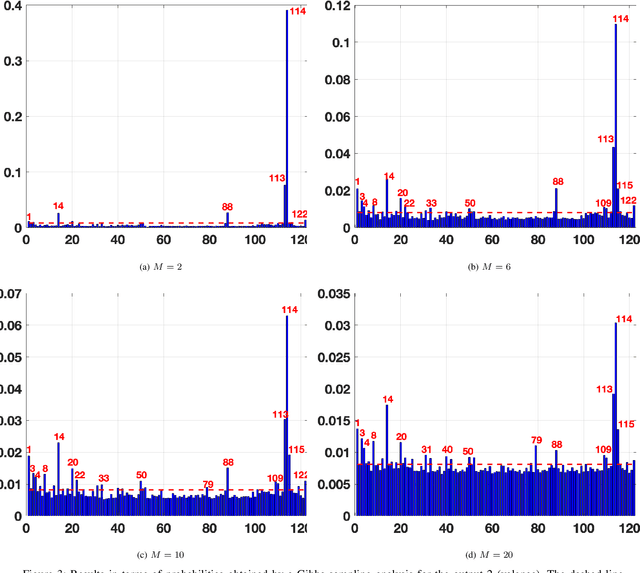
In the last decade, soundscapes have become one of the most active topics in Acoustics, providing a holistic approach to the acoustic environment, which involves human perception and context. Soundscapes-elicited emotions are central and substantially subtle and unnoticed (compared to speech or music). Currently, soundscape emotion recognition is a very active topic in the literature. We provide an exhaustive variable selection study (i.e., a selection of the soundscapes indicators) to a well-known dataset (emo-soundscapes). We consider linear soundscape emotion models for two soundscapes descriptors: arousal and valence. Several ranking schemes and procedures for selecting the number of variables are applied. We have also performed an alternating optimization scheme for obtaining the best sequences keeping fixed a certain number of features. Furthermore, we have designed a novel technique based on Gibbs sampling, which provides a more complete and clear view of the relevance of each variable. Finally, we have also compared our results with the analysis obtained by the classical methods based on p-values. As a result of our study, we suggest two simple and parsimonious linear models of only 7 and 16 variables (within the 122 possible features) for the two outputs (arousal and valence), respectively. The suggested linear models provide very good and competitive performance, with $R^2>0.86$ and $R^2>0.63$ (values obtained after a cross-validation procedure), respectively.

On the safe use of prior densities for Bayesian model selection

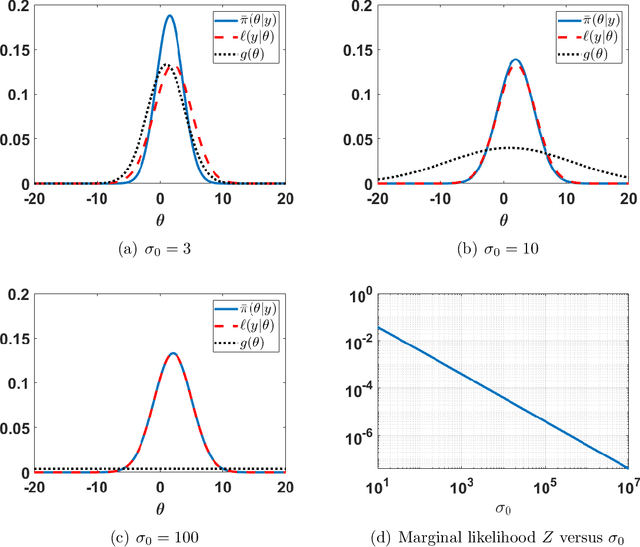
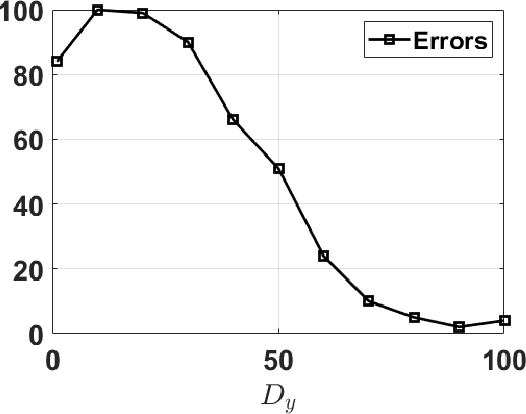
The application of Bayesian inference for the purpose of model selection is very popular nowadays. In this framework, models are compared through their marginal likelihoods, or their quotients, called Bayes factors. However, marginal likelihoods depends on the prior choice. For model selection, even diffuse priors can be actually very informative, unlike for the parameter estimation problem. Furthermore, when the prior is improper, the marginal likelihood of the corresponding model is undetermined. In this work, we discuss the issue of prior sensitivity of the marginal likelihood and its role in model selection. We also comment on the use of uninformative priors, which are very common choices in practice. Several practical suggestions are discussed and many possible solutions, proposed in the literature, to design objective priors for model selection are described. Some of them also allow the use of improper priors. The connection between the marginal likelihood approach and the well-known information criteria is also presented. We describe the main issues and possible solutions by illustrative numerical examples, providing also some related code. One of them involving a real-world application on exoplanet detection.

A survey of Monte Carlo methods for noisy and costly densities with application to reinforcement learning

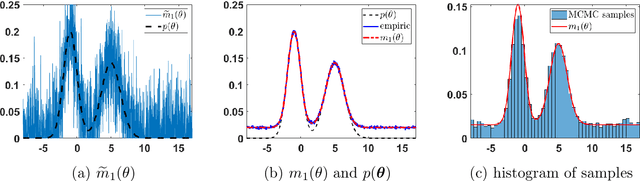
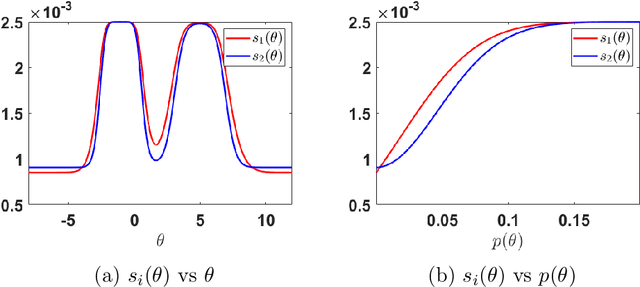
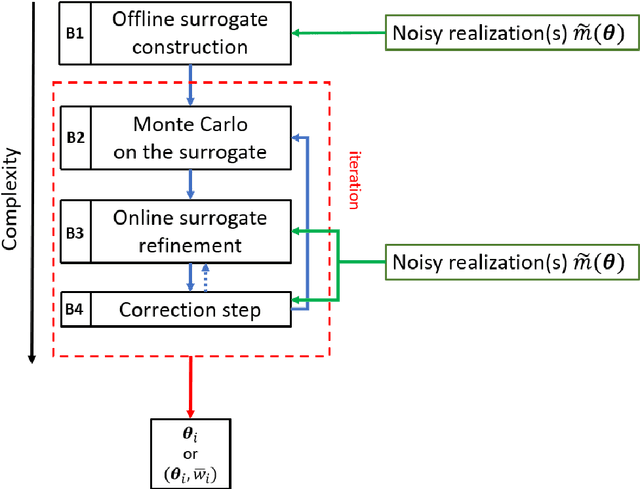
This survey gives an overview of Monte Carlo methodologies using surrogate models, for dealing with densities which are intractable, costly, and/or noisy. This type of problem can be found in numerous real-world scenarios, including stochastic optimization and reinforcement learning, where each evaluation of a density function may incur some computationally-expensive or even physical (real-world activity) cost, likely to give different results each time. The surrogate model does not incur this cost, but there are important trade-offs and considerations involved in the choice and design of such methodologies. We classify the different methodologies into three main classes and describe specific instances of algorithms under a unified notation. A modular scheme which encompasses the considered methods is also presented. A range of application scenarios is discussed, with special attention to the likelihood-free setting and reinforcement learning. Several numerical comparisons are also provided.

A Survey of Monte Carlo Methods for Parameter Estimation

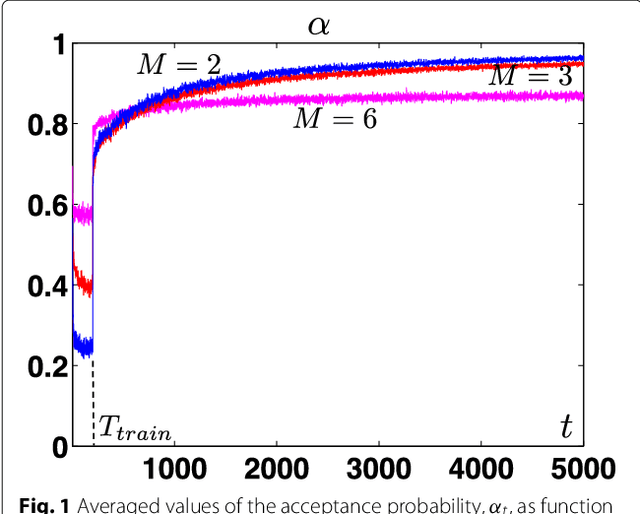
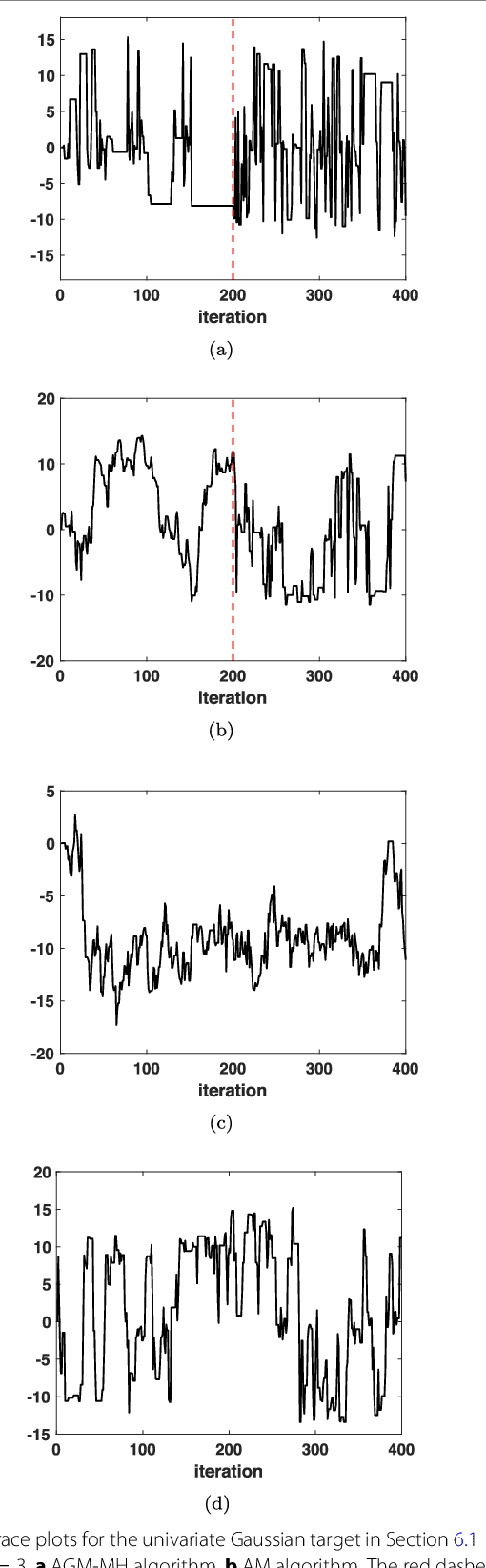
Statistical signal processing applications usually require the estimation of some parameters of interest given a set of observed data. These estimates are typically obtained either by solving a multi-variate optimization problem, as in the maximum likelihood (ML) or maximum a posteriori (MAP) estimators, or by performing a multi-dimensional integration, as in the minimum mean squared error (MMSE) estimators. Unfortunately, analytical expressions for these estimators cannot be found in most real-world applications, and the Monte Carlo (MC) methodology is one feasible approach. MC methods proceed by drawing random samples, either from the desired distribution or from a simpler one, and using them to compute consistent estimators. The most important families of MC algorithms are Markov chain MC (MCMC) and importance sampling (IS). On the one hand, MCMC methods draw samples from a proposal density, building then an ergodic Markov chain whose stationary distribution is the desired distribution by accepting or rejecting those candidate samples as the new state of the chain. On the other hand, IS techniques draw samples from a simple proposal density, and then assign them suitable weights that measure their quality in some appropriate way. In this paper, we perform a thorough review of MC methods for the estimation of static parameters in signal processing applications. A historical note on the development of MC schemes is also provided, followed by the basic MC method and a brief description of the rejection sampling (RS) algorithm, as well as three sections describing many of the most relevant MCMC and IS algorithms, and their combined use.

Automatic tempered posterior distributions for Bayesian inversion problems

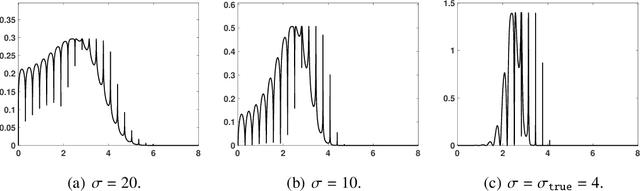
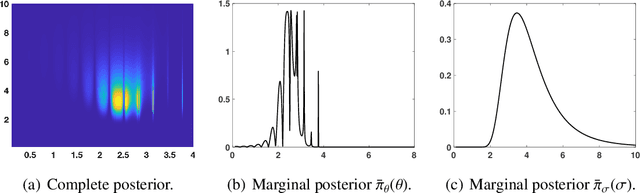
We propose a novel adaptive importance sampling scheme for Bayesian inversion problems where the inference of the variables of interest and the power of the data noise is split. More specifically, we consider a Bayesian analysis for the variables of interest (i.e., the parameters of the model to invert), whereas we employ a maximum likelihood approach for the estimation of the noise power. The whole technique is implemented by means of an iterative procedure, alternating sampling and optimization steps. Moreover, the noise power is also used as a tempered parameter for the posterior distribution of the the variables of interest. Therefore, a sequence of tempered posterior densities is generated, where the tempered parameter is automatically selected according to the actual estimation of the noise power. A complete Bayesian study over the model parameters and the scale parameter can be also performed. Numerical experiments show the benefits of the proposed approach.

MCMC-driven importance samplers

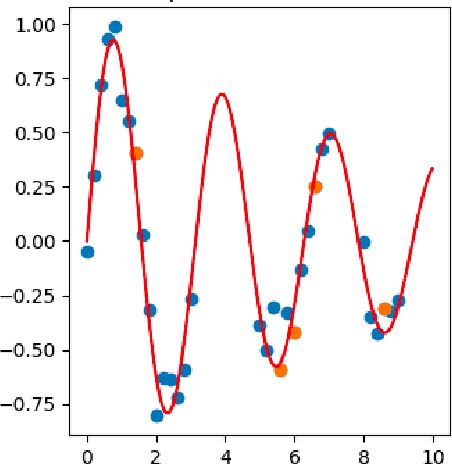
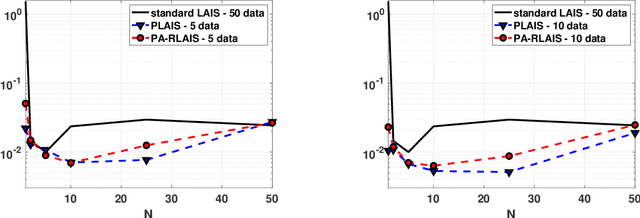
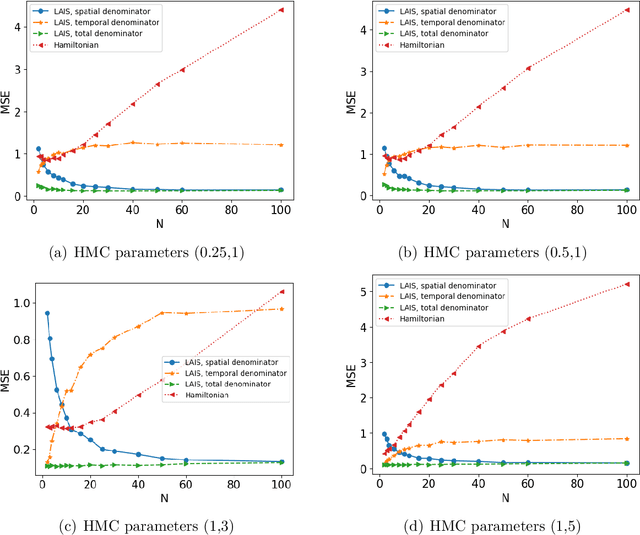
Monte Carlo methods are the standard procedure for estimating complicated integrals of multidimensional Bayesian posterior distributions. In this work, we focus on LAIS, a class of adaptive importance samplers where Markov chain Monte Carlo (MCMC) algorithms are employed to drive an underlying multiple importance sampling (IS) scheme. Its power lies in the simplicity of the layered framework: the upper layer locates proposal densities by means of MCMC algorithms; while the lower layer handles the multiple IS scheme, in order to compute the final estimators. The modular nature of LAIS allows for different possible choices in the upper and lower layers, that will have different performance and computational costs. In this work, we propose different enhancements in order to increase the efficiency and reduce the computational cost, of both upper and lower layers. The different variants are essential if we aim to address computational challenges arising in real-world applications, such as highly concentrated posterior distributions (due to large amounts of data, etc.). Hamiltonian-driven importance samplers are presented and tested. Furthermore, we introduce different strategies for designing cheaper schemes, for instance, recycling samples generated in the upper layer and using them in the final estimators in the lower layer. Numerical experiments show the benefits of the proposed schemes as compared to the vanilla version of LAIS and other benchmark methods.

Deep Importance Sampling based on Regression for Model Inversion and Emulation

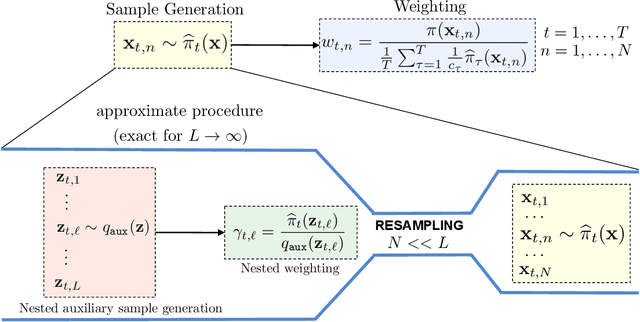
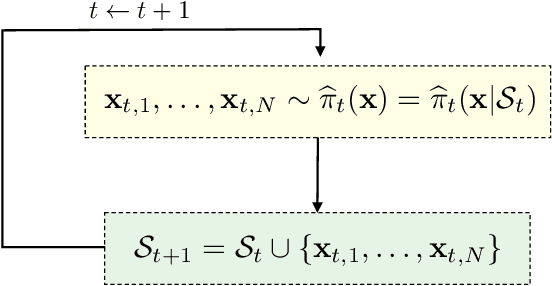
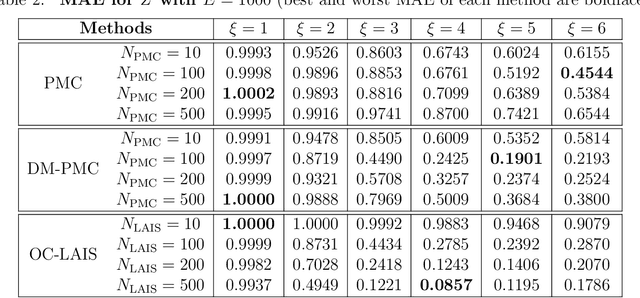
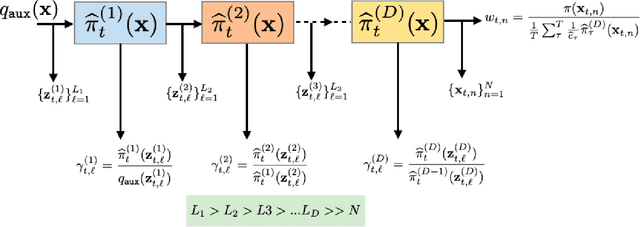
Understanding systems by forward and inverse modeling is a recurrent topic of research in many domains of science and engineering. In this context, Monte Carlo methods have been widely used as powerful tools for numerical inference and optimization. They require the choice of a suitable proposal density that is crucial for their performance. For this reason, several adaptive importance sampling (AIS) schemes have been proposed in the literature. We here present an AIS framework called Regression-based Adaptive Deep Importance Sampling (RADIS). In RADIS, the key idea is the adaptive construction via regression of a non-parametric proposal density (i.e., an emulator), which mimics the posterior distribution and hence minimizes the mismatch between proposal and target densities. RADIS is based on a deep architecture of two (or more) nested IS schemes, in order to draw samples from the constructed emulator. The algorithm is highly efficient since employs the posterior approximation as proposal density, which can be improved adding more support points. As a consequence, RADIS asymptotically converges to an exact sampler under mild conditions. Additionally, the emulator produced by RADIS can be in turn used as a cheap surrogate model for further studies. We introduce two specific RADIS implementations that use Gaussian Processes (GPs) and Nearest Neighbors (NN) for constructing the emulator. Several numerical experiments and comparisons show the benefits of the proposed schemes. A real-world application in remote sensing model inversion and emulation confirms the validity of the approach.