Let's consider more general nonlinear approaches to study teleconnections of climate variables

The recent work by (Rieger et al 2021) is concerned with the problem of extracting features from spatio-temporal geophysical signals. The authors introduce the complex rotated MCA (xMCA) to deal with lagged effects and non-orthogonality of the feature representation. This method essentially (1) transforms the signals to a complex plane with the Hilbert transform; (2) applies an oblique (Varimax and Promax) rotation to remove the orthogonality constraint; and (3) performs the eigendecomposition in this complex space (Horel et al, 1984). We argue that this method is essentially a particular case of the method called rotated complex kernel principal component analysis (ROCK-PCA) introduced in (Bueso et al., 2019, 2020), where we proposed the same approach: first transform the data to the complex plane with the Hilbert transform and then apply the varimax rotation, with the only difference that the eigendecomposition is performed in the dual (kernel) Hilbert space. The latter allows us to generalize the xMCA solution by extracting nonlinear (curvilinear) features when nonlinear kernel functions are used. Hence, the solution of xMCA boils down to ROCK-PCA when the inner product is computed in the input data space instead of in the high-dimensional (possibly infinite) kernel Hilbert space to which data has been mapped. In this short correspondence we show theoretical proof that xMCA is a special case of ROCK-PCA and provide quantitative evidence that more expressive and informative features can be extracted when working with kernels; results of the decomposition of global sea surface temperature (SST) fields are shown to illustrate the capabilities of ROCK-PCA to cope with nonlinear processes, unlike xMCA.

Machine Learning Information Fusion in Earth Observation: A Comprehensive Review of Methods, Applications and Data Sources

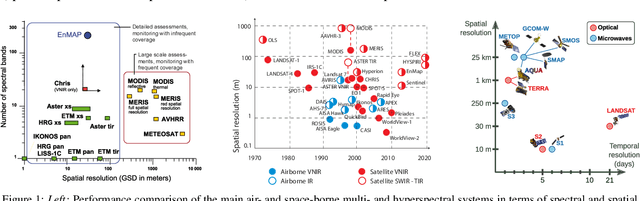
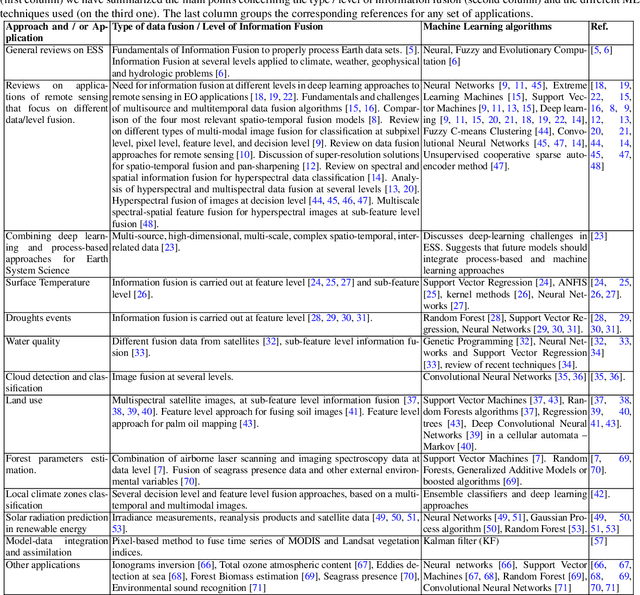
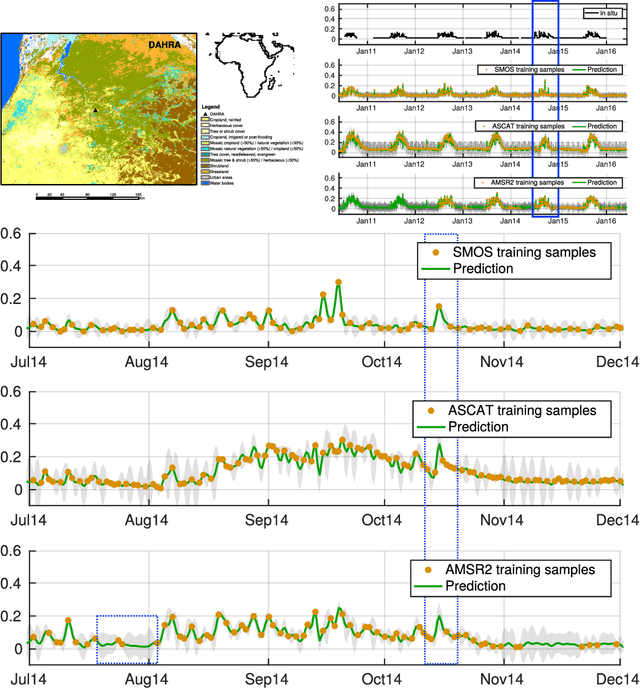
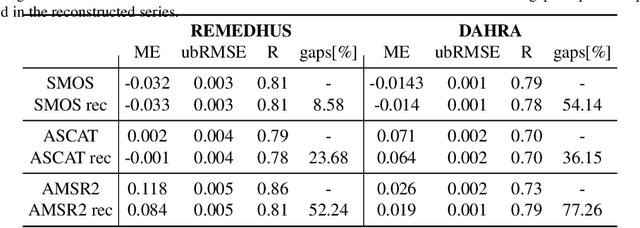
This paper reviews the most important information fusion data-driven algorithms based on Machine Learning (ML) techniques for problems in Earth observation. Nowadays we observe and model the Earth with a wealth of observations, from a plethora of different sensors, measuring states, fluxes, processes and variables, at unprecedented spatial and temporal resolutions. Earth observation is well equipped with remote sensing systems, mounted on satellites and airborne platforms, but it also involves in-situ observations, numerical models and social media data streams, among other data sources. Data-driven approaches, and ML techniques in particular, are the natural choice to extract significant information from this data deluge. This paper produces a thorough review of the latest work on information fusion for Earth observation, with a practical intention, not only focusing on describing the most relevant previous works in the field, but also the most important Earth observation applications where ML information fusion has obtained significant results. We also review some of the most currently used data sets, models and sources for Earth observation problems, describing their importance and how to obtain the data when needed. Finally, we illustrate the application of ML data fusion with a representative set of case studies, as well as we discuss and outlook the near future of the field.

Deep Importance Sampling based on Regression for Model Inversion and Emulation

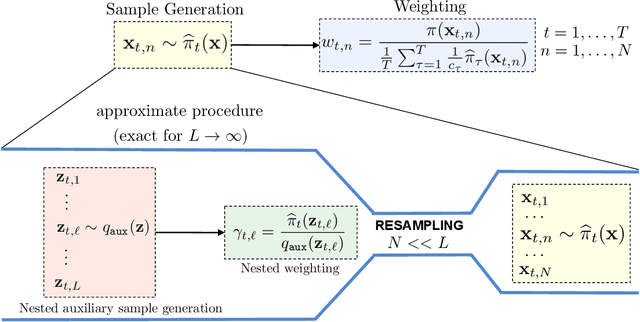
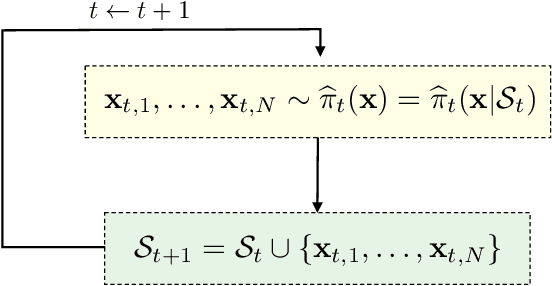
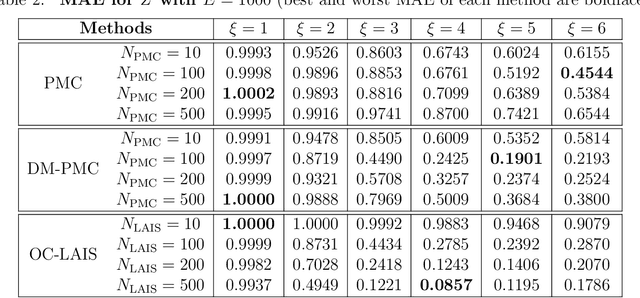
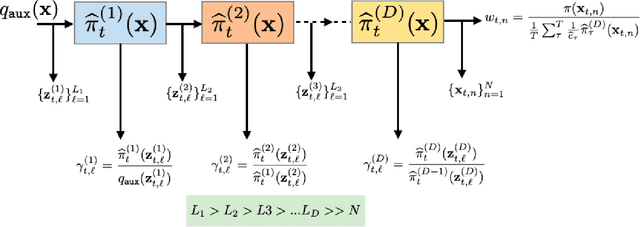
Understanding systems by forward and inverse modeling is a recurrent topic of research in many domains of science and engineering. In this context, Monte Carlo methods have been widely used as powerful tools for numerical inference and optimization. They require the choice of a suitable proposal density that is crucial for their performance. For this reason, several adaptive importance sampling (AIS) schemes have been proposed in the literature. We here present an AIS framework called Regression-based Adaptive Deep Importance Sampling (RADIS). In RADIS, the key idea is the adaptive construction via regression of a non-parametric proposal density (i.e., an emulator), which mimics the posterior distribution and hence minimizes the mismatch between proposal and target densities. RADIS is based on a deep architecture of two (or more) nested IS schemes, in order to draw samples from the constructed emulator. The algorithm is highly efficient since employs the posterior approximation as proposal density, which can be improved adding more support points. As a consequence, RADIS asymptotically converges to an exact sampler under mild conditions. Additionally, the emulator produced by RADIS can be in turn used as a cheap surrogate model for further studies. We introduce two specific RADIS implementations that use Gaussian Processes (GPs) and Nearest Neighbors (NN) for constructing the emulator. Several numerical experiments and comparisons show the benefits of the proposed schemes. A real-world application in remote sensing model inversion and emulation confirms the validity of the approach.

Group Importance Sampling for Particle Filtering and MCMC

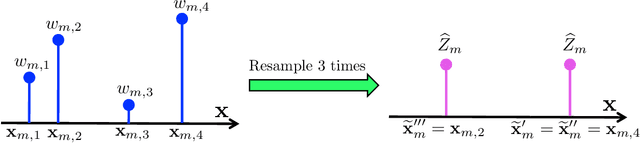
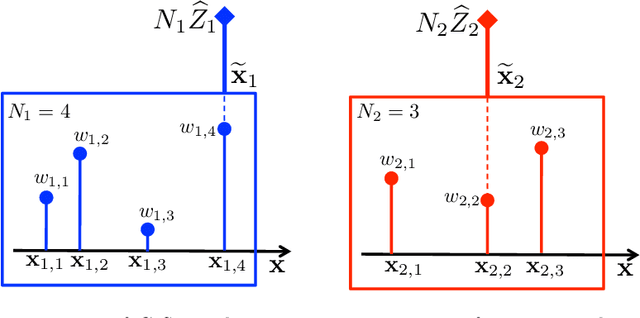
Bayesian methods and their implementations by means of sophisticated Monte Carlo techniques have become very popular in signal processing over the last years. Importance Sampling (IS) is a well-known Monte Carlo technique that approximates integrals involving a posterior distribution by means of weighted samples. In this work, we study the assignation of a single weighted sample which compresses the information contained in a population of weighted samples. Part of the theory that we present as Group Importance Sampling (GIS) has been employed implicitly in different works in the literature. The provided analysis yields several theoretical and practical consequences. For instance, we discuss the application of GIS into the Sequential Importance Resampling framework and show that Independent Multiple Try Metropolis schemes can be interpreted as a standard Metropolis-Hastings algorithm, following the GIS approach. We also introduce two novel Markov Chain Monte Carlo (MCMC) techniques based on GIS. The first one, named Group Metropolis Sampling method, produces a Markov chain of sets of weighted samples. All these sets are then employed for obtaining a unique global estimator. The second one is the Distributed Particle Metropolis-Hastings technique, where different parallel particle filters are jointly used to drive an MCMC algorithm. Different resampled trajectories are compared and then tested with a proper acceptance probability. The novel schemes are tested in different numerical experiments such as learning the hyperparameters of Gaussian Processes, two localization problems in a wireless sensor network (with synthetic and real data) and the tracking of vegetation parameters given satellite observations, where they are compared with several benchmark Monte Carlo techniques. Three illustrative Matlab demos are also provided.