Moni Naor
Private Everlasting Prediction
May 16, 2023Abstract:A private learner is trained on a sample of labeled points and generates a hypothesis that can be used for predicting the labels of newly sampled points while protecting the privacy of the training set [Kasiviswannathan et al., FOCS 2008]. Research uncovered that private learners may need to exhibit significantly higher sample complexity than non-private learners as is the case with, e.g., learning of one-dimensional threshold functions [Bun et al., FOCS 2015, Alon et al., STOC 2019]. We explore prediction as an alternative to learning. Instead of putting forward a hypothesis, a predictor answers a stream of classification queries. Earlier work has considered a private prediction model with just a single classification query [Dwork and Feldman, COLT 2018]. We observe that when answering a stream of queries, a predictor must modify the hypothesis it uses over time, and, furthermore, that it must use the queries for this modification, hence introducing potential privacy risks with respect to the queries themselves. We introduce private everlasting prediction taking into account the privacy of both the training set and the (adaptively chosen) queries made to the predictor. We then present a generic construction of private everlasting predictors in the PAC model. The sample complexity of the initial training sample in our construction is quadratic (up to polylog factors) in the VC dimension of the concept class. Our construction allows prediction for all concept classes with finite VC dimension, and in particular threshold functions with constant size initial training sample, even when considered over infinite domains, whereas it is known that the sample complexity of privately learning threshold functions must grow as a function of the domain size and hence is impossible for infinite domains.
Adversarial Laws of Large Numbers and Optimal Regret in Online Classification
Jan 22, 2021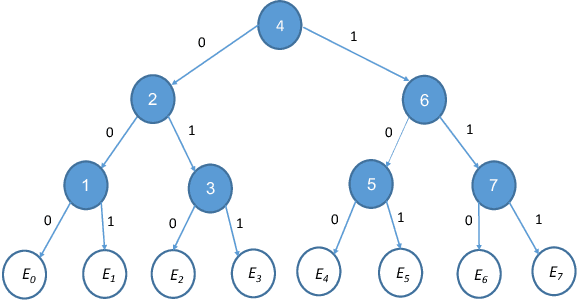
Abstract:Laws of large numbers guarantee that given a large enough sample from some population, the measure of any fixed sub-population is well-estimated by its frequency in the sample. We study laws of large numbers in sampling processes that can affect the environment they are acting upon and interact with it. Specifically, we consider the sequential sampling model proposed by Ben-Eliezer and Yogev (2020), and characterize the classes which admit a uniform law of large numbers in this model: these are exactly the classes that are \emph{online learnable}. Our characterization may be interpreted as an online analogue to the equivalence between learnability and uniform convergence in statistical (PAC) learning. The sample-complexity bounds we obtain are tight for many parameter regimes, and as an application, we determine the optimal regret bounds in online learning, stated in terms of \emph{Littlestone's dimension}, thus resolving the main open question from Ben-David, P\'al, and Shalev-Shwartz (2009), which was also posed by Rakhlin, Sridharan, and Tewari (2015).
Privately Learning Thresholds: Closing the Exponential Gap
Nov 22, 2019
Abstract:We study the sample complexity of learning threshold functions under the constraint of differential privacy. It is assumed that each labeled example in the training data is the information of one individual and we would like to come up with a generalizing hypothesis $h$ while guaranteeing differential privacy for the individuals. Intuitively, this means that any single labeled example in the training data should not have a significant effect on the choice of the hypothesis. This problem has received much attention recently; unlike the non-private case, where the sample complexity is independent of the domain size and just depends on the desired accuracy and confidence, for private learning the sample complexity must depend on the domain size $X$ (even for approximate differential privacy). Alon et al. (STOC 2019) showed a lower bound of $\Omega(\log^*|X|)$ on the sample complexity and Bun et al. (FOCS 2015) presented an approximate-private learner with sample complexity $\tilde{O}\left(2^{\log^*|X|}\right)$. In this work we reduce this gap significantly, almost settling the sample complexity. We first present a new upper bound (algorithm) of $\tilde{O}\left(\left(\log^*|X|\right)^2\right)$ on the sample complexity and then present an improved version with sample complexity $\tilde{O}\left(\left(\log^*|X|\right)^{1.5}\right)$. Our algorithm is constructed for the related interior point problem, where the goal is to find a point between the largest and smallest input elements. It is based on selecting an input-dependent hash function and using it to embed the database into a domain whose size is reduced logarithmically; this results in a new database, an interior point of which can be used to generate an interior point in the original database in a differentially private manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge