The Nonstochastic Control Problem

We consider the problem of controlling an unknown linear dynamical system in the presence of (nonstochastic) adversarial perturbations and adversarial convex loss functions. In contrast to classical control, the a priori determination of an optimal controller here is hindered by the latter's dependence on the yet unknown perturbations and costs. Instead, we measure regret against an optimal linear policy in hindsight, and give the first efficient algorithm that guarantees a sublinear regret bound, scaling as T^{2/3}, in this setting.

Logarithmic Regret for Online Control

We study optimal regret bounds for control in linear dynamical systems under adversarially changing strongly convex cost functions, given the knowledge of transition dynamics. This includes several well studied and fundamental frameworks such as the Kalman filter and the linear quadratic regulator. State of the art methods achieve regret which scales as $O(\sqrt{T})$, where $T$ is the time horizon. We show that the optimal regret in this setting can be significantly smaller, scaling as $O(\text{poly}(\log T))$. This regret bound is achieved by two different efficient iterative methods, online gradient descent and online natural gradient.

Predicting Animation Skeletons for 3D Articulated Models via Volumetric Nets

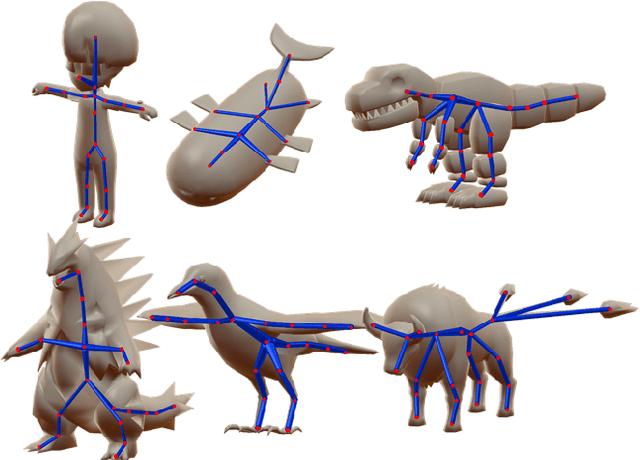
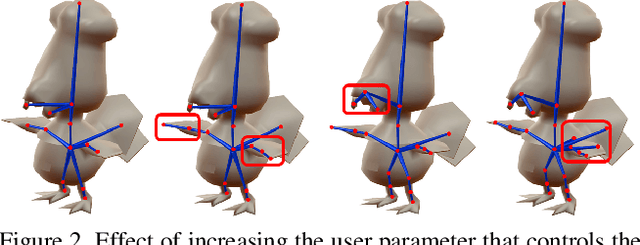
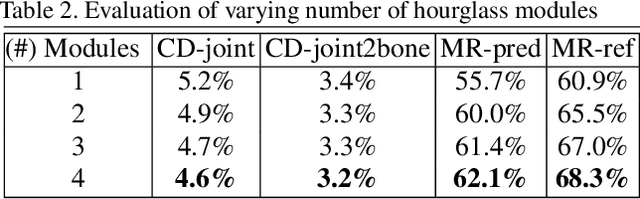
We present a learning method for predicting animation skeletons for input 3D models of articulated characters. In contrast to previous approaches that fit pre-defined skeleton templates or predict fixed sets of joints, our method produces an animation skeleton tailored for the structure and geometry of the input 3D model. Our architecture is based on a stack of hourglass modules trained on a large dataset of 3D rigged characters mined from the web. It operates on the volumetric representation of the input 3D shapes augmented with geometric shape features that provide additional cues for joint and bone locations. Our method also enables intuitive user control of the level-of-detail for the output skeleton. Our evaluation demonstrates that our approach predicts animation skeletons that are much more similar to the ones created by humans compared to several alternatives and baselines.

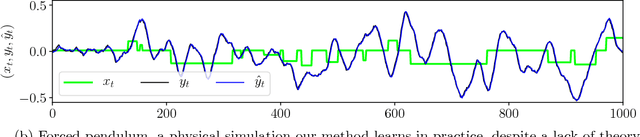
Online Control with Adversarial Disturbances

We study the control of a linear dynamical system with adversarial disturbances (as opposed to statistical noise). The objective we consider is one of regret: we desire an online control procedure that can do nearly as well as that of a procedure that has full knowledge of the disturbances in hindsight. Our main result is an efficient algorithm that provides nearly tight regret bounds for this problem. From a technical standpoint, this work generalizes upon previous work in two main aspects: our model allows for adversarial noise in the dynamics, and allows for general convex costs.

Provably Efficient Maximum Entropy Exploration

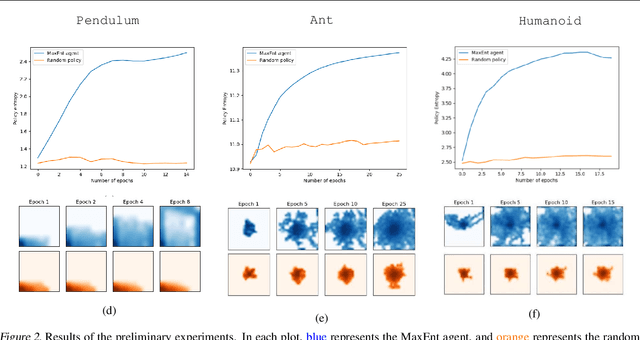
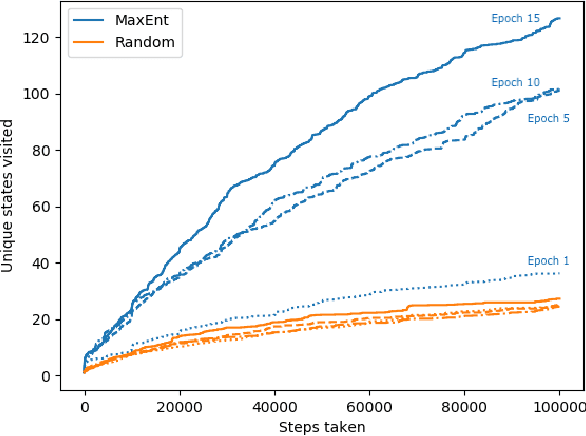
Suppose an agent is in a (possibly unknown) Markov decision process (MDP) in the absence of a reward signal, what might we hope that an agent can efficiently learn to do? One natural, intrinsically defined, objective problem is for the agent to learn a policy which induces a distribution over state space that is as uniform as possible, which can be measured in an entropic sense. Despite the corresponding mathematical program being non-convex, our main result provides a provably efficient method (both in terms of sample size and computational complexity) to construct such a maximum-entropy exploratory policy. Key to our algorithmic methodology is utilizing the conditional gradient method (a.k.a. the Frank-Wolfe algorithm) which utilizes an approximate MDP solver.

The Case for Full-Matrix Adaptive Regularization

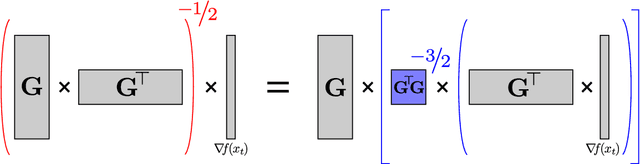
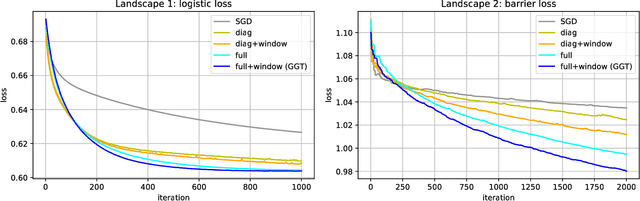
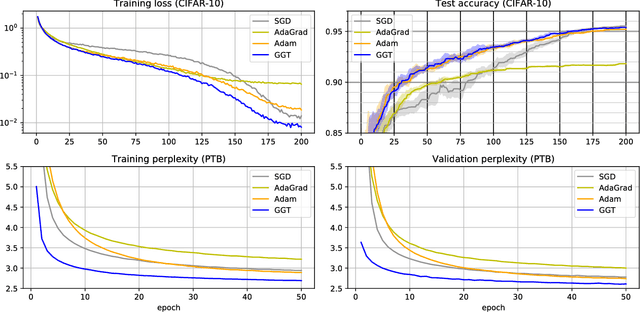
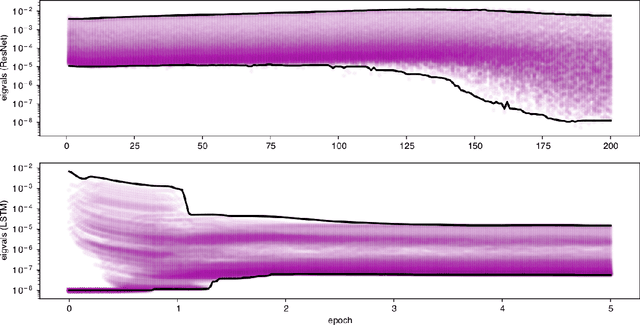
Adaptive regularization methods come in diagonal and full-matrix variants. However, only the former have enjoyed widespread adoption in training large-scale deep models. This is due to the computational overhead of manipulating a full matrix in high dimension. In this paper, we show how to make full-matrix adaptive regularization practical and useful. We present GGT, a truly scalable full-matrix adaptive optimizer. At the heart of our algorithm is an efficient method for computing the inverse square root of a low-rank matrix. We show that GGT converges to first-order local minima, providing the first rigorous theoretical analysis of adaptive regularization in non-convex optimization. In preliminary experiments, GGT trains faster across a variety of synthetic tasks and standard deep learning benchmarks.

Color Sails: Discrete-Continuous Palettes for Deep Color Exploration

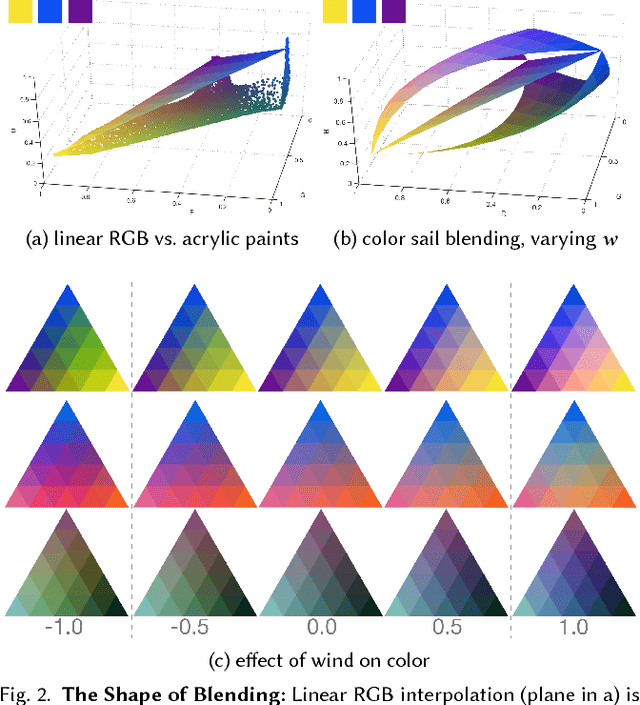
We present color sails, a discrete-continuous color gamut representation that extends the color gradient analogy to three dimensions and allows interactive control of the color blending behavior. Our representation models a wide variety of color distributions in a compact manner, and lends itself to applications such as color exploration for graphic design, illustration and similar fields. We propose a Neural Network that can fit a color sail to any image. Then, the user can adjust color sail parameters to change the base colors, their blending behavior and the number of colors, exploring a wide range of options for the original design. In addition, we propose a Deep Learning model that learns to automatically segment an image into color-compatible alpha masks, each equipped with its own color sail. This allows targeted color exploration by either editing their corresponding color sails or using standard software packages. Our model is trained on a custom diverse dataset of art and design. We provide both quantitative evaluations, and a user study, demonstrating the effectiveness of color sail interaction. Interactive demos are available at www.colorsails.com.

Spectral Filtering for General Linear Dynamical Systems

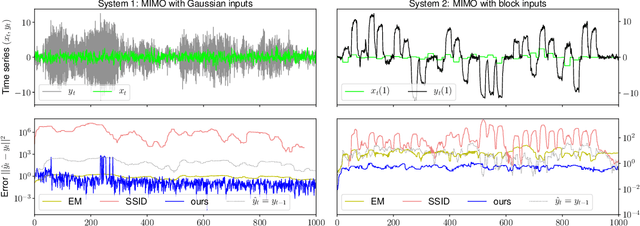
We give a polynomial-time algorithm for learning latent-state linear dynamical systems without system identification, and without assumptions on the spectral radius of the system's transition matrix. The algorithm extends the recently introduced technique of spectral filtering, previously applied only to systems with a symmetric transition matrix, using a novel convex relaxation to allow for the efficient identification of phases.

Learning Linear Dynamical Systems via Spectral Filtering

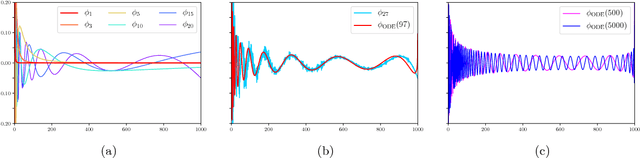
We present an efficient and practical algorithm for the online prediction of discrete-time linear dynamical systems with a symmetric transition matrix. We circumvent the non-convex optimization problem using improper learning: carefully overparameterize the class of LDSs by a polylogarithmic factor, in exchange for convexity of the loss functions. From this arises a polynomial-time algorithm with a near-optimal regret guarantee, with an analogous sample complexity bound for agnostic learning. Our algorithm is based on a novel filtering technique, which may be of independent interest: we convolve the time series with the eigenvectors of a certain Hankel matrix.

Efficient Regret Minimization in Non-Convex Games

We consider regret minimization in repeated games with non-convex loss functions. Minimizing the standard notion of regret is computationally intractable. Thus, we define a natural notion of regret which permits efficient optimization and generalizes offline guarantees for convergence to an approximate local optimum. We give gradient-based methods that achieve optimal regret, which in turn guarantee convergence to equilibrium in this framework.