General reproducing properties in RKHS with application to derivative and integral operators

In this paper, we generalize the reproducing property in Reproducing Kernel Hilbert Spaces (RKHS). We establish a reproducing property for the closure of the class of combinations of composition operators under minimal conditions. As an application, we improve the existing sufficient conditions for the reproducing property to hold for the derivative operator, as well as for the existence of the mean embedding function. These results extend the scope of applicability of the representer theorem for regularized learning algorithms that involve data for function values, gradients, or any other operator from the considered class.

Learning signals defined on graphs with optimal transport and Gaussian process regression

In computational physics, machine learning has now emerged as a powerful complementary tool to explore efficiently candidate designs in engineering studies. Outputs in such supervised problems are signals defined on meshes, and a natural question is the extension of general scalar output regression models to such complex outputs. Changes between input geometries in terms of both size and adjacency structure in particular make this transition non-trivial. In this work, we propose an innovative strategy for Gaussian process regression where inputs are large and sparse graphs with continuous node attributes and outputs are signals defined on the nodes of the associated inputs. The methodology relies on the combination of regularized optimal transport, dimension reduction techniques, and the use of Gaussian processes indexed by graphs. In addition to enabling signal prediction, the main point of our proposal is to come with confidence intervals on node values, which is crucial for uncertainty quantification and active learning. Numerical experiments highlight the efficiency of the method to solve real problems in fluid dynamics and solid mechanics.

Taming Score-Based Diffusion Priors for Infinite-Dimensional Nonlinear Inverse Problems

This work introduces a sampling method capable of solving Bayesian inverse problems in function space. It does not assume the log-concavity of the likelihood, meaning that it is compatible with nonlinear inverse problems. The method leverages the recently defined infinite-dimensional score-based diffusion models as a learning-based prior, while enabling provable posterior sampling through a Langevin-type MCMC algorithm defined on function spaces. A novel convergence analysis is conducted, inspired by the fixed-point methods established for traditional regularization-by-denoising algorithms and compatible with weighted annealing. The obtained convergence bound explicitly depends on the approximation error of the score; a well-approximated score is essential to obtain a well-approximated posterior. Stylized and PDE-based examples are provided, demonstrating the validity of our convergence analysis. We conclude by presenting a discussion of the method's challenges related to learning the score and computational complexity.

Gaussian process regression with Sliced Wasserstein Weisfeiler-Lehman graph kernels

Supervised learning has recently garnered significant attention in the field of computational physics due to its ability to effectively extract complex patterns for tasks like solving partial differential equations, or predicting material properties. Traditionally, such datasets consist of inputs given as meshes with a large number of nodes representing the problem geometry (seen as graphs), and corresponding outputs obtained with a numerical solver. This means the supervised learning model must be able to handle large and sparse graphs with continuous node attributes. In this work, we focus on Gaussian process regression, for which we introduce the Sliced Wasserstein Weisfeiler-Lehman (SWWL) graph kernel. In contrast to existing graph kernels, the proposed SWWL kernel enjoys positive definiteness and a drastic complexity reduction, which makes it possible to process datasets that were previously impossible to handle. The new kernel is first validated on graph classification for molecular datasets, where the input graphs have a few tens of nodes. The efficiency of the SWWL kernel is then illustrated on graph regression in computational fluid dynamics and solid mechanics, where the input graphs are made up of tens of thousands of nodes.

Automated approach for source location in shallow waters

This paper proposes a fully automated method for recovering the location of a source and medium parameters in shallow waters. The scenario involves an unknown source emitting low-frequency sound waves in a shallow water environment, and a single hydrophone recording the signal. Firstly, theoretical tools are introduced to understand the robustness of the warping method and to propose and analyze an automated way to separate the modal components of the recorded signal. Secondly, using the spectrogram of each modal component, the paper investigates the best way to recover the modal travel times and provides stability estimates. Finally, a penalized minimization algorithm is presented to recover estimates of the source location and medium parameters. The proposed method is tested on experimental data of right whale gunshot and combustive sound sources, demonstrating its effectiveness in real-world scenarios.

Conditional score-based diffusion models for Bayesian inference in infinite dimensions

Since their first introduction, score-based diffusion models (SDMs) have been successfully applied to solve a variety of linear inverse problems in finite-dimensional vector spaces due to their ability to efficiently approximate the posterior distribution. However, using SDMs for inverse problems in infinite-dimensional function spaces has only been addressed recently and by learning the unconditional score. While this approach has some advantages, depending on the specific inverse problem at hand, in order to sample from the conditional distribution it needs to incorporate the information from the observed data with a proximal optimization step, solving an optimization problem numerous times. This may not be feasible in inverse problems with computationally costly forward operators. To address these limitations, in this work we propose a method to learn the posterior distribution in infinite-dimensional Bayesian linear inverse problems using amortized conditional SDMs. In particular, we prove that the conditional denoising estimator is a consistent estimator of the conditional score in infinite dimensions. We show that the extension of SDMs to the conditional setting requires some care because the conditional score typically blows up for small times contrarily to the unconditional score. We also discuss the robustness of the learned distribution against perturbations of the observations. We conclude by presenting numerical examples that validate our approach and provide additional insights.

Multi-output Gaussian processes for inverse uncertainty quantification in neutron noise analysis

In a fissile material, the inherent multiplicity of neutrons born through induced fissions leads to correlations in their detection statistics. The correlations between neutrons can be used to trace back some characteristics of the fissile material. This technique known as neutron noise analysis has applications in nuclear safeguards or waste identification. It provides a non-destructive examination method for an unknown fissile material. This is an example of an inverse problem where the cause is inferred from observations of the consequences. However, neutron correlation measurements are often noisy because of the stochastic nature of the underlying processes. This makes the resolution of the inverse problem more complex since the measurements are strongly dependent on the material characteristics. A minor change in the material properties can lead to very different outputs. Such an inverse problem is said to be ill-posed. For an ill-posed inverse problem the inverse uncertainty quantification is crucial. Indeed, seemingly low noise in the data can lead to strong uncertainties in the estimation of the material properties. Moreover, the analytical framework commonly used to describe neutron correlations relies on strong physical assumptions and is thus inherently biased. This paper addresses dual goals. Firstly, surrogate models are used to improve neutron correlations predictions and quantify the errors on those predictions. Then, the inverse uncertainty quantification is performed to include the impact of measurement error alongside the residual model bias.

Heterogeneous Treatment Effects Estimation: When Machine Learning meets multiple treatment regime

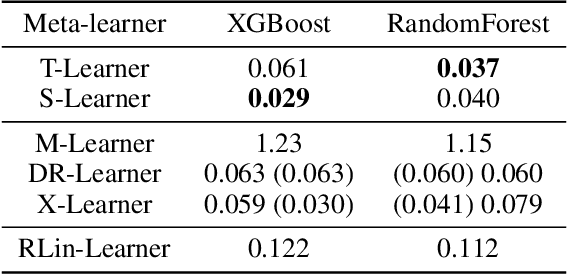
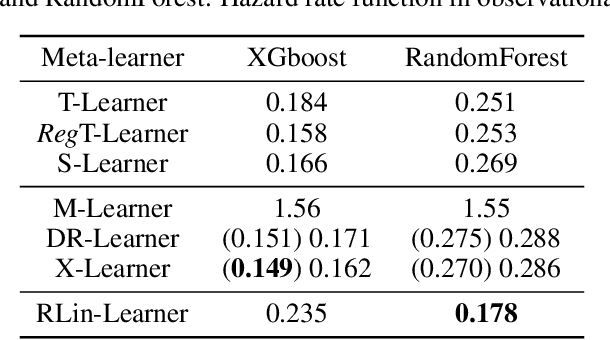
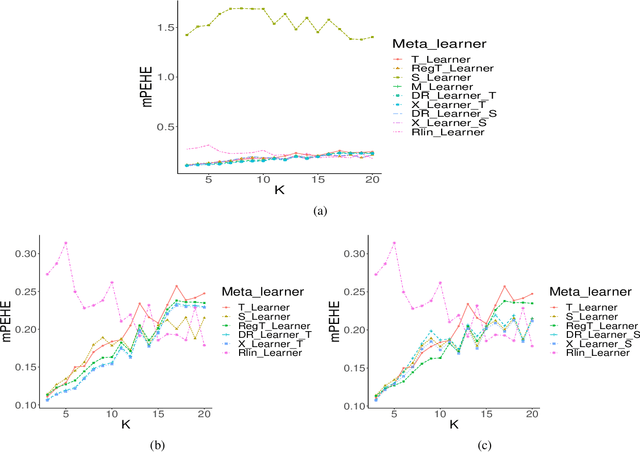
In many scientific and engineering domains, inferring the effect of treatment and exploring its heterogeneity is crucial for optimization and decision making. In addition to Machine Learning based models (e.g. Random Forests or Neural Networks), many meta-algorithms have been developed to estimate the Conditional Average Treatment Effect (CATE) function in the binary setting, with the main advantage of not restraining the estimation to a specific supervised learning method. However, this task becomes more challenging when the treatment is not binary. In this paper, we investigate the Rubin Causal Model under the multi-treatment regime and we focus on estimating heterogeneous treatment effects. We generalize \textit{Meta-learning} algorithms to estimate the CATE for each possible treatment value. Using synthetic and semi-synthetic simulation datasets, we assess the quality of each meta-learner in observational data, and we highlight in particular the performances of the X-learner.

Adaptive importance sampling for seismic fragility curve estimation

As part of Probabilistic Risk Assessment studies, it is necessary to study the fragility of mechanical and civil engineered structures when subjected to seismic loads. This risk can be measured with fragility curves, which express the probability of failure of the structure conditionally to a seismic intensity measure. The estimation of fragility curves relies on time-consuming numerical simulations, so that careful experimental design is required in order to gain the maximum information on the structure's fragility with a limited number of code evaluations. We propose and implement an active learning methodology based on adaptive importance sampling in order to reduce the variance of the training loss. The efficiency of the proposed method in terms of bias, standard deviation and prediction interval coverage are theoretically and numerically characterized.

Imaging in random media by two-point coherent interferometry

This paper considers wave-based imaging through a heterogeneous (random) scattering medium. The goal is to estimate the support of the reflectivity function of a remote scene from measurements of the backscattered wave field. The proposed imaging methodology is based on the coherent interferometric (CINT) approach that exploits the local empirical cross correlations of the measurements of the wave field. The standard CINT images are known to be robust (statistically stable) with respect to the random medium, but the stability comes at the expense of a loss of resolution. This paper shows that a two-point CINT function contains the information needed to obtain statistically stable and high-resolution images. Different methods to build such images are presented, theoretically analyzed and compared with the standard imaging approaches using numerical simulations. The first method involves a phase-retrieval step to extract the reflectivity function from the modulus of its Fourier transform. The second method involves the evaluation of the leading eigenvector of the two-point CINT imaging function seen as the kernel of a linear operator. The third method uses an optimization step to extract the reflectivity function from some cross products of its Fourier transform. The presentation is for the synthetic aperture radar data acquisition setup, where a moving sensor probes the scene with signals emitted periodically and records the resulting backscattered wave. The generalization to other imaging setups, with passive or active arrays of sensors, is discussed briefly.