Learning signals defined on graphs with optimal transport and Gaussian process regression

In computational physics, machine learning has now emerged as a powerful complementary tool to explore efficiently candidate designs in engineering studies. Outputs in such supervised problems are signals defined on meshes, and a natural question is the extension of general scalar output regression models to such complex outputs. Changes between input geometries in terms of both size and adjacency structure in particular make this transition non-trivial. In this work, we propose an innovative strategy for Gaussian process regression where inputs are large and sparse graphs with continuous node attributes and outputs are signals defined on the nodes of the associated inputs. The methodology relies on the combination of regularized optimal transport, dimension reduction techniques, and the use of Gaussian processes indexed by graphs. In addition to enabling signal prediction, the main point of our proposal is to come with confidence intervals on node values, which is crucial for uncertainty quantification and active learning. Numerical experiments highlight the efficiency of the method to solve real problems in fluid dynamics and solid mechanics.

Gaussian process regression with Sliced Wasserstein Weisfeiler-Lehman graph kernels

Supervised learning has recently garnered significant attention in the field of computational physics due to its ability to effectively extract complex patterns for tasks like solving partial differential equations, or predicting material properties. Traditionally, such datasets consist of inputs given as meshes with a large number of nodes representing the problem geometry (seen as graphs), and corresponding outputs obtained with a numerical solver. This means the supervised learning model must be able to handle large and sparse graphs with continuous node attributes. In this work, we focus on Gaussian process regression, for which we introduce the Sliced Wasserstein Weisfeiler-Lehman (SWWL) graph kernel. In contrast to existing graph kernels, the proposed SWWL kernel enjoys positive definiteness and a drastic complexity reduction, which makes it possible to process datasets that were previously impossible to handle. The new kernel is first validated on graph classification for molecular datasets, where the input graphs have a few tens of nodes. The efficiency of the SWWL kernel is then illustrated on graph regression in computational fluid dynamics and solid mechanics, where the input graphs are made up of tens of thousands of nodes.

Quantitative performance evaluation of Bayesian neural networks

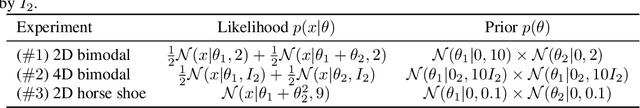
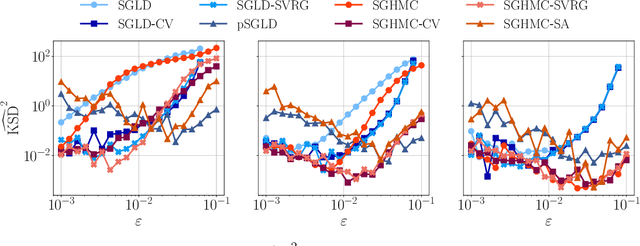
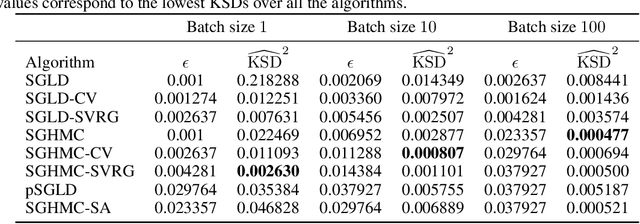
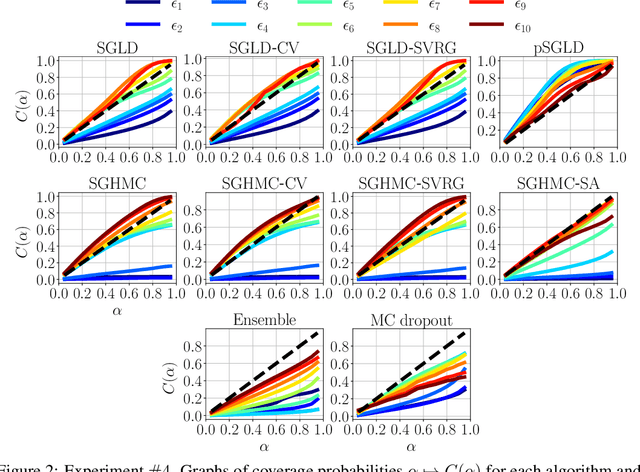
Due to the growing adoption of deep neural networks in many fields of science and engineering, modeling and estimating their uncertainties has become of primary importance. Various approaches have been investigated including Bayesian neural networks, ensembles, deterministic approximations, amongst others. Despite the growing litterature about uncertainty quantification in deep learning, the quality of the uncertainty estimates remains an open question. In this work, we attempt to assess the performance of several algorithms on sampling and regression tasks by evaluating the quality of the confidence regions and how well the generated samples are representative of the unknown target distribution. Towards this end, several sampling and regression tasks are considered, and the selected algorithms are compared in terms of coverage probabilities, kernelized Stein discrepancies, and maximum mean discrepancies.

SHAFF: Fast and consistent SHApley eFfect estimates via random Forests

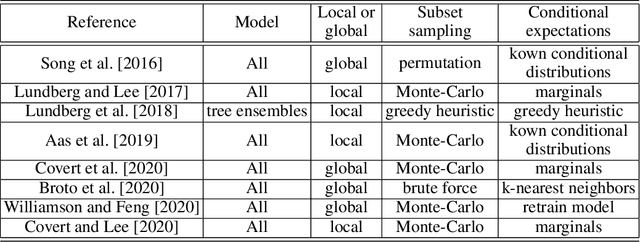
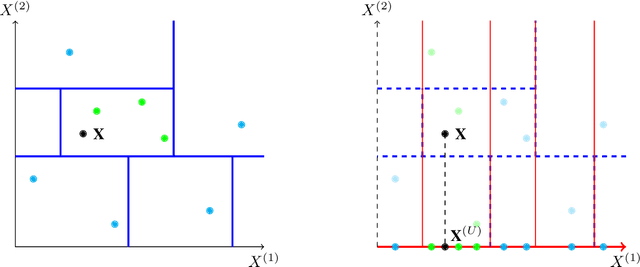
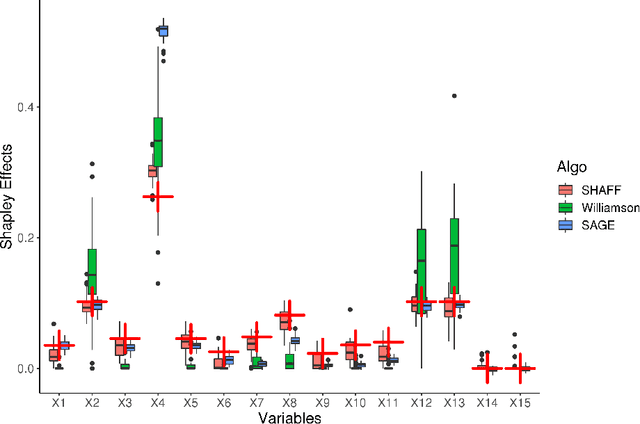
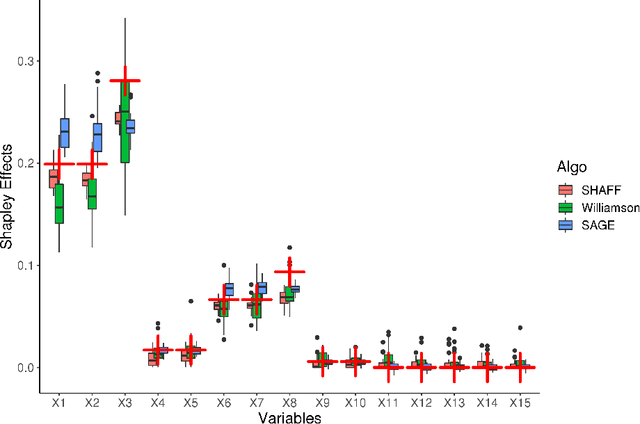
Interpretability of learning algorithms is crucial for applications involving critical decisions, and variable importance is one of the main interpretation tools. Shapley effects are now widely used to interpret both tree ensembles and neural networks, as they can efficiently handle dependence and interactions in the data, as opposed to most other variable importance measures. However, estimating Shapley effects is a challenging task, because of the computational complexity and the conditional expectation estimates. Accordingly, existing Shapley algorithms have flaws: a costly running time, or a bias when input variables are dependent. Therefore, we introduce SHAFF, SHApley eFfects via random Forests, a fast and accurate Shapley effect estimate, even when input variables are dependent. We show SHAFF efficiency through both a theoretical analysis of its consistency, and the practical performance improvements over competitors with extensive experiments. An implementation of SHAFF in C++ and R is available online.

MDA for random forests: inconsistency, and a practical solution via the Sobol-MDA

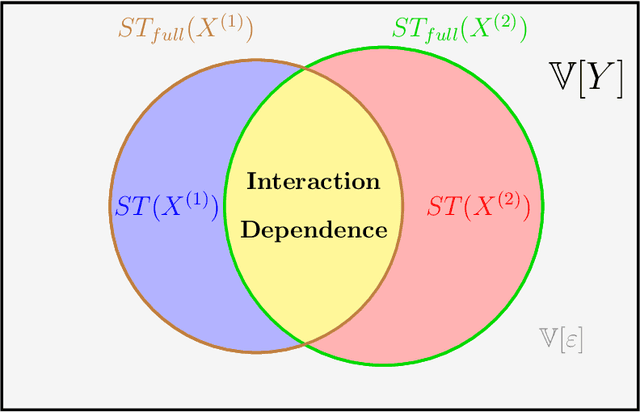
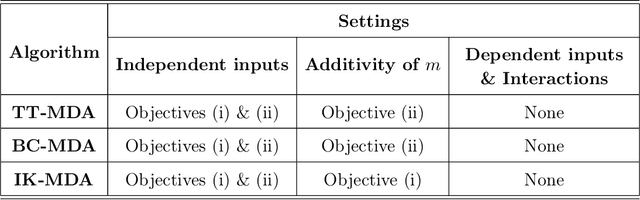
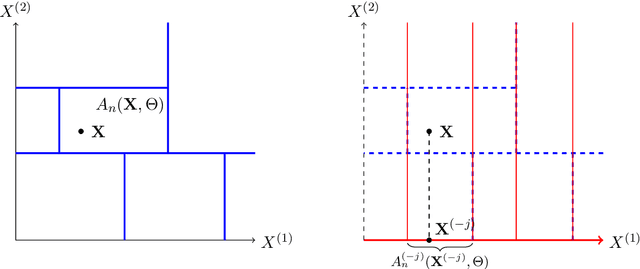
Variable importance measures are the main tools to analyze the black-box mechanism of random forests. Although the Mean Decrease Accuracy (MDA) is widely accepted as the most efficient variable importance measure for random forests, little is known about its theoretical properties. In fact, the exact MDA definition varies across the main random forest software. In this article, our objective is to rigorously analyze the behavior of the main MDA implementations. Consequently, we mathematically formalize the various implemented MDA algorithms, and then establish their limits when the sample size increases. In particular, we break down these limits in three components: the first two are related to Sobol indices, which are well-defined measures of a variable contribution to the output variance, widely used in the sensitivity analysis field, as opposed to the third term, whose value increases with dependence within input variables. Thus, we theoretically demonstrate that the MDA does not target the right quantity when inputs are dependent, a fact that has already been noticed experimentally. To address this issue, we define a new importance measure for random forests, the Sobol-MDA, which fixes the flaws of the original MDA. We prove the consistency of the Sobol-MDA and show its good empirical performance through experiments on both simulated and real data. An open source implementation in R and C++ is available online.

Interpretable Random Forests via Rule Extraction

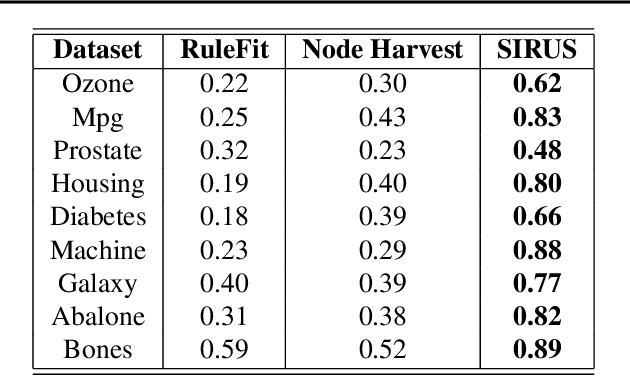
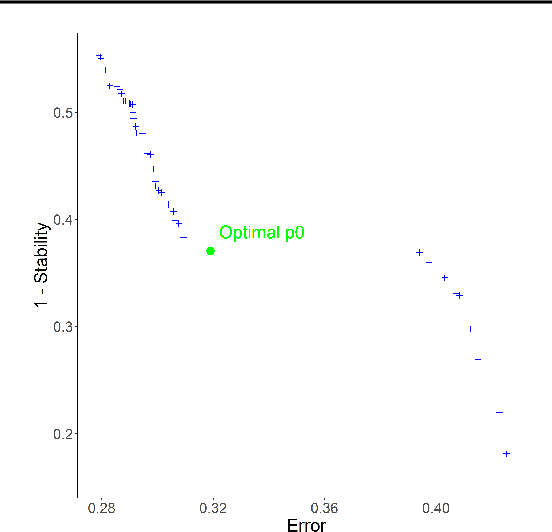
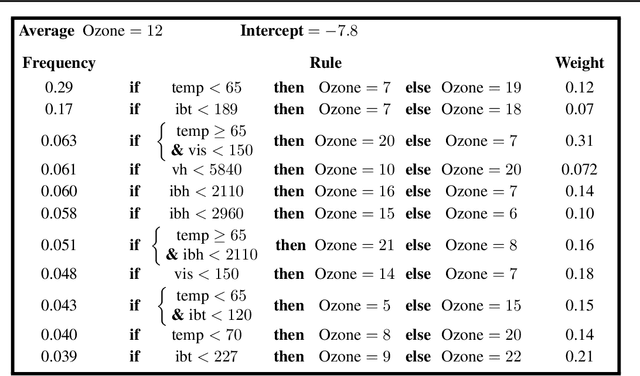
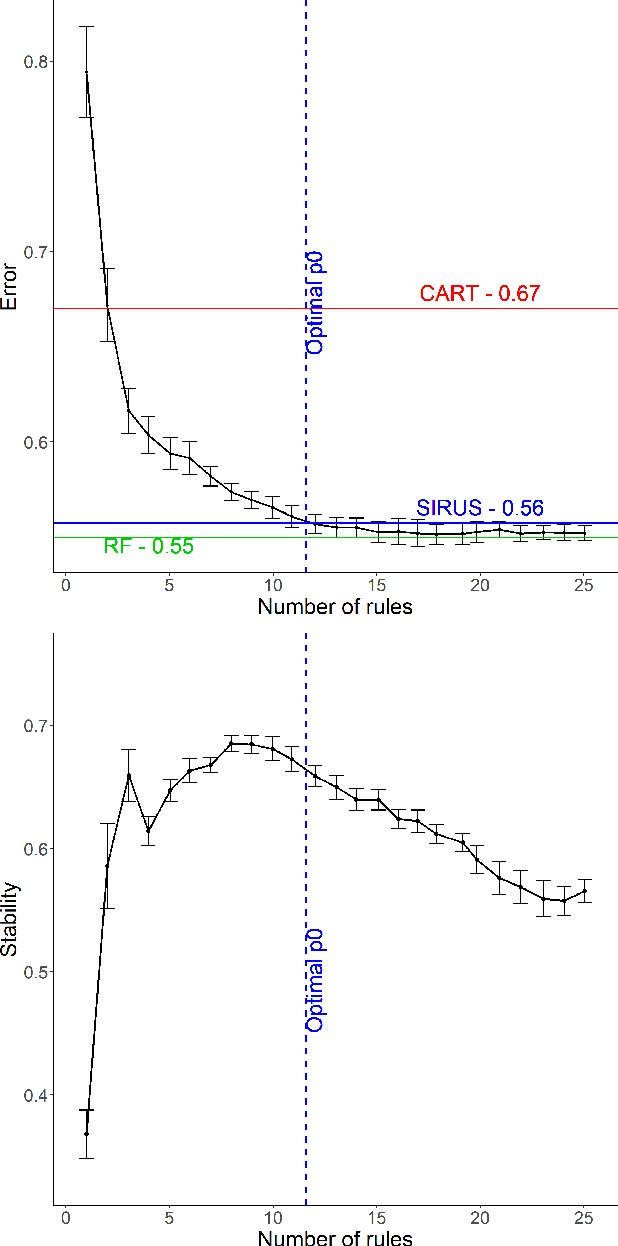
We introduce SIRUS (Stable and Interpretable RUle Set) for regression, a stable rule learning algorithm which takes the form of a short and simple list of rules. State-of-the-art learning algorithms are often referred to as "black boxes" because of the high number of operations involved in their prediction process. Despite their powerful predictivity, this lack of interpretability may be highly restrictive for applications with critical decisions at stake. On the other hand, algorithms with a simple structure-typically decision trees, rule algorithms, or sparse linear models-are well known for their instability. This undesirable feature makes the conclusions of the data analysis unreliable and turns out to be a strong operational limitation. This motivates the design of SIRUS, which combines a simple structure with a remarkable stable behavior when data is perturbed. The algorithm is based on random forests, the predictive accuracy of which is preserved. We demonstrate the efficiency of the method both empirically (through experiments) and theoretically (with the proof of its asymptotic stability). Our R/C++ software implementation sirus is available from CRAN.

Towards new cross-validation-based estimators for Gaussian process regression: efficient adjoint computation of gradients

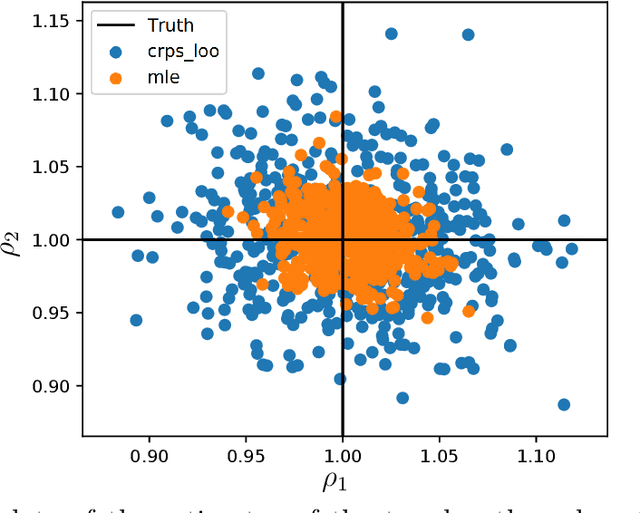
We consider the problem of estimating the parameters of the covariance function of a Gaussian process by cross-validation. We suggest using new cross-validation criteria derived from the literature of scoring rules. We also provide an efficient method for computing the gradient of a cross-validation criterion. To the best of our knowledge, our method is more efficient than what has been proposed in the literature so far. It makes it possible to lower the complexity of jointly evaluating leave-one-out criteria and their gradients.

SIRUS: Making Random Forests Interpretable

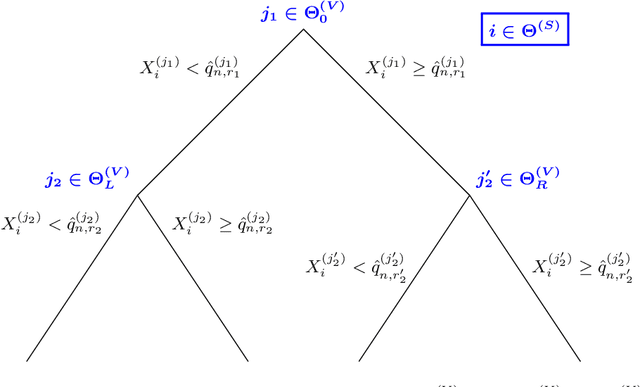
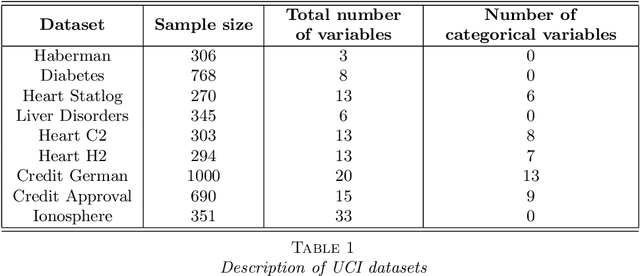
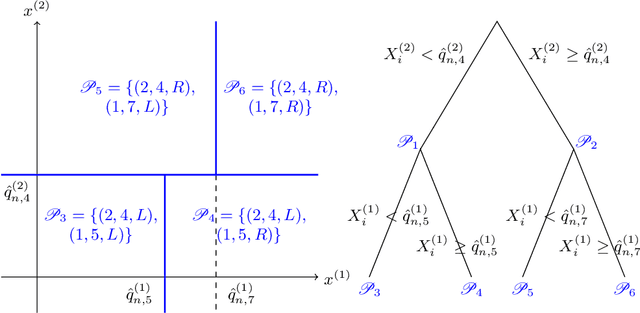
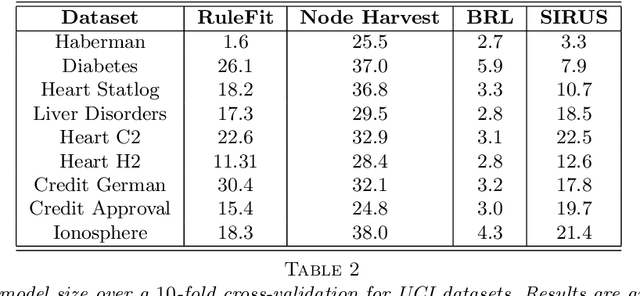
State-of-the-art learning algorithms, such as random forests or neural networks, are often qualified as ''black-boxes'' because of the high number and complexity of operations involved in their prediction mechanism. This lack of interpretability is a strong limitation for applications involving critical decisions, typically the analysis of production processes in the manufacturing industry. In such critical contexts, models have to be interpretable, i.e., simple, stable, and predictive. To address this issue, we design SIRUS (Stable and Interpretable RUle Set), a new classification algorithm based on random forests, which takes the form of a short list of rules. While simple models are usually unstable with respect to data perturbation, SIRUS achieves a remarkable stability improvement over cutting-edge methods. Furthermore, SIRUS inherits a predictive accuracy close to random forests, combined with the simplicity of decision trees. These properties are assessed both from a theoretical and empirical point of view, through extensive numerical experiments based on our R/C++ software implementation sirus available from CRAN.