Distributional encoding for Gaussian process regression with qualitative inputs

Gaussian Process (GP) regression is a popular and sample-efficient approach for many engineering applications, where observations are expensive to acquire, and is also a central ingredient of Bayesian optimization (BO), a highly prevailing method for the optimization of black-box functions. However, when all or some input variables are categorical, building a predictive and computationally efficient GP remains challenging. Starting from the naive target encoding idea, where the original categorical values are replaced with the mean of the target variable for that category, we propose a generalization based on distributional encoding (DE) which makes use of all samples of the target variable for a category. To handle this type of encoding inside the GP, we build upon recent results on characteristic kernels for probability distributions, based on the maximum mean discrepancy and the Wasserstein distance. We also discuss several extensions for classification, multi-task learning and incorporation or auxiliary information. Our approach is validated empirically, and we demonstrate state-of-the-art predictive performance on a variety of synthetic and real-world datasets. DE is naturally complementary to recent advances in BO over discrete and mixed-spaces.

Kernel Stein Discrepancy thinning: a theoretical perspective of pathologies and a practical fix with regularization

Stein thinning is a promising algorithm proposed by (Riabiz et al., 2022) for post-processing outputs of Markov chain Monte Carlo (MCMC). The main principle is to greedily minimize the kernelized Stein discrepancy (KSD), which only requires the gradient of the log-target distribution, and is thus well-suited for Bayesian inference. The main advantages of Stein thinning are the automatic remove of the burn-in period, the correction of the bias introduced by recent MCMC algorithms, and the asymptotic properties of convergence towards the target distribution. Nevertheless, Stein thinning suffers from several empirical pathologies, which may result in poor approximations, as observed in the literature. In this article, we conduct a theoretical analysis of these pathologies, to clearly identify the mechanisms at stake, and suggest improved strategies. Then, we introduce the regularized Stein thinning algorithm to alleviate the identified pathologies. Finally, theoretical guarantees and extensive experiments show the high efficiency of the proposed algorithm.

A sampling criterion for constrained Bayesian optimization with uncertainties

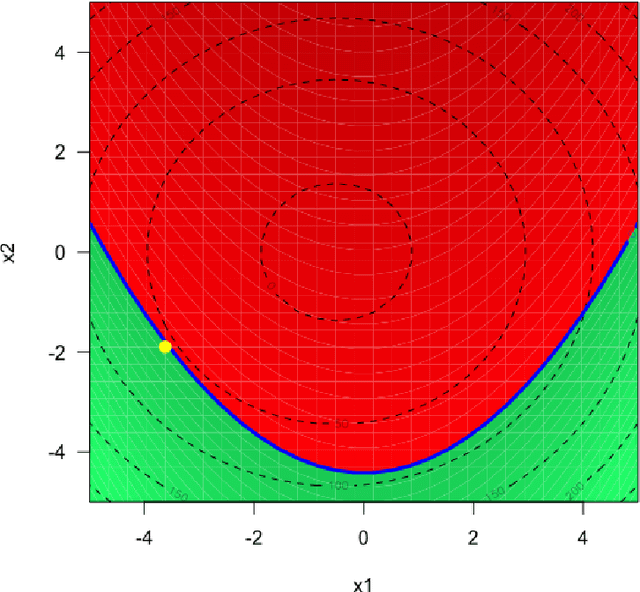
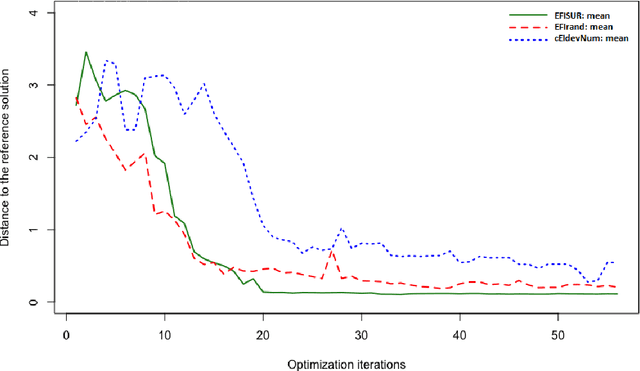
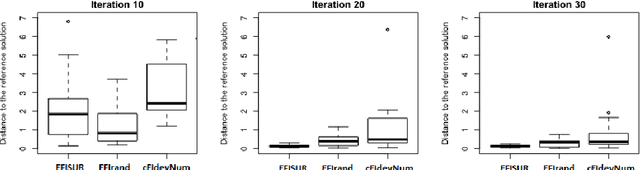
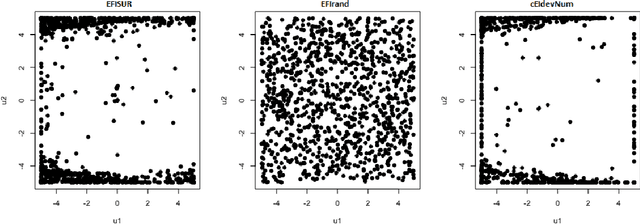
We consider the problem of chance constrained optimization where it is sought to optimize a function and satisfy constraints, both of which are affected by uncertainties. The real world declinations of this problem are particularly challenging because of their inherent computational cost. To tackle such problems, we propose a new Bayesian optimization method. It applies to the situation where the uncertainty comes from some of the inputs, so that it becomes possible to define an acquisition criterion in the joint controlled-uncontrolled input space. The main contribution of this work is an acquisition criterion that accounts for both the average improvement in objective function and the constraint reliability. The criterion is derived following the Stepwise Uncertainty Reduction logic and its maximization provides both optimal controlled and uncontrolled parameters. Analytical expressions are given to efficiently calculate the criterion. Numerical studies on test functions are presented. It is found through experimental comparisons with alternative sampling criteria that the adequation between the sampling criterion and the problem contributes to the efficiency of the overall optimization. As a side result, an expression for the variance of the improvement is given.

Global Sensitivity Analysis with Dependence Measures

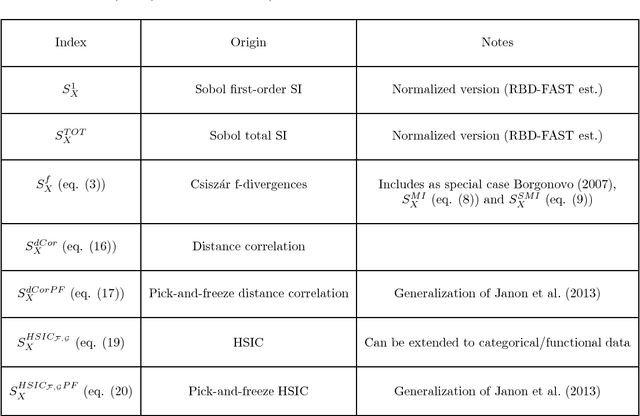
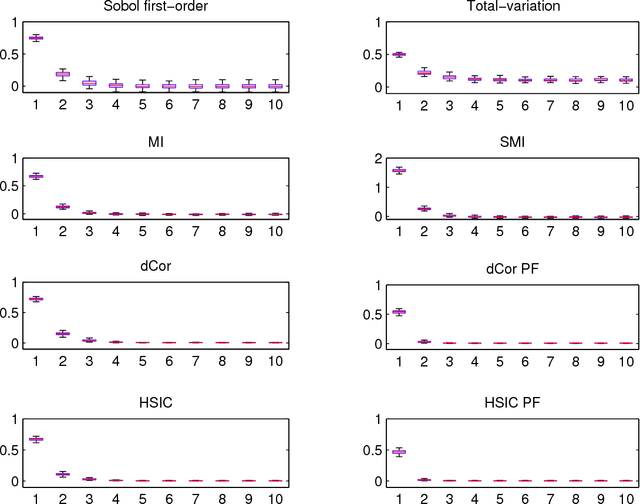
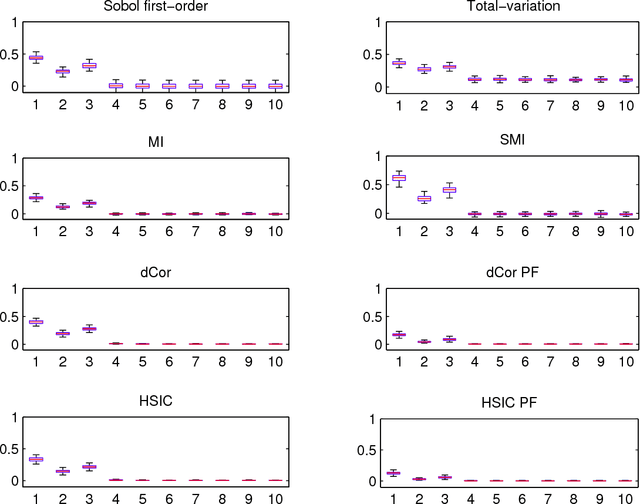
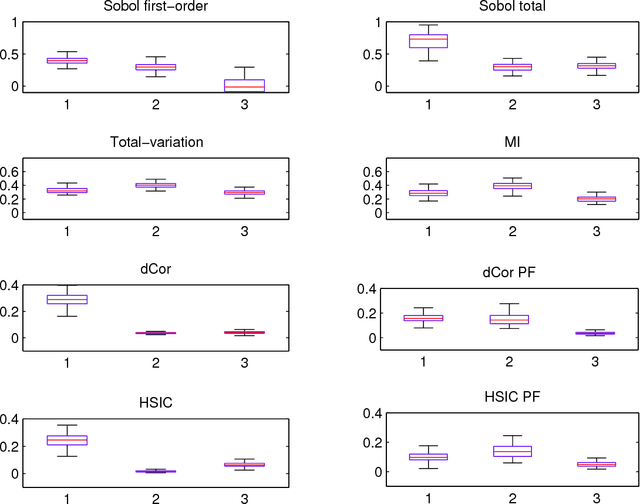
Global sensitivity analysis with variance-based measures suffers from several theoretical and practical limitations, since they focus only on the variance of the output and handle multivariate variables in a limited way. In this paper, we introduce a new class of sensitivity indices based on dependence measures which overcomes these insufficiencies. Our approach originates from the idea to compare the output distribution with its conditional counterpart when one of the input variables is fixed. We establish that this comparison yields previously proposed indices when it is performed with Csiszar f-divergences, as well as sensitivity indices which are well-known dependence measures between random variables. This leads us to investigate completely new sensitivity indices based on recent state-of-the-art dependence measures, such as distance correlation and the Hilbert-Schmidt independence criterion. We also emphasize the potential of feature selection techniques relying on such dependence measures as alternatives to screening in high dimension.