Scalable and adaptive prediction bands with kernel sum-of-squares

Conformal Prediction (CP) is a popular framework for constructing prediction bands with valid coverage in finite samples, while being free of any distributional assumption. A well-known limitation of conformal prediction is the lack of adaptivity, although several works introduced practically efficient alternate procedures. In this work, we build upon recent ideas that rely on recasting the CP problem as a statistical learning problem, directly targeting coverage and adaptivity. This statistical learning problem is based on reproducible kernel Hilbert spaces (RKHS) and kernel sum-of-squares (SoS) methods. First, we extend previous results with a general representer theorem and exhibit the dual formulation of the learning problem. Crucially, such dual formulation can be solved efficiently by accelerated gradient methods with several hundreds or thousands of samples, unlike previous strategies based on off-the-shelf semidefinite programming algorithms. Second, we introduce a new hyperparameter tuning strategy tailored specifically to target adaptivity through bounds on test-conditional coverage. This strategy, based on the Hilbert-Schmidt Independence Criterion (HSIC), is introduced here to tune kernel lengthscales in our framework, but has broader applicability since it could be used in any CP algorithm where the score function is learned. Finally, extensive experiments are conducted to show how our method compares to related work. All figures can be reproduced with the accompanying code.

Physics-Learning AI Datamodel (PLAID) datasets: a collection of physics simulations for machine learning

Machine learning-based surrogate models have emerged as a powerful tool to accelerate simulation-driven scientific workflows. However, their widespread adoption is hindered by the lack of large-scale, diverse, and standardized datasets tailored to physics-based simulations. While existing initiatives provide valuable contributions, many are limited in scope-focusing on specific physics domains, relying on fragmented tooling, or adhering to overly simplistic datamodels that restrict generalization. To address these limitations, we introduce PLAID (Physics-Learning AI Datamodel), a flexible and extensible framework for representing and sharing datasets of physics simulations. PLAID defines a unified standard for describing simulation data and is accompanied by a library for creating, reading, and manipulating complex datasets across a wide range of physical use cases (gitlab.com/drti/plaid). We release six carefully crafted datasets under the PLAID standard, covering structural mechanics and computational fluid dynamics, and provide baseline benchmarks using representative learning methods. Benchmarking tools are made available on Hugging Face, enabling direct participation by the community and contribution to ongoing evaluation efforts (huggingface.co/PLAIDcompetitions).

Learning signals defined on graphs with optimal transport and Gaussian process regression

In computational physics, machine learning has now emerged as a powerful complementary tool to explore efficiently candidate designs in engineering studies. Outputs in such supervised problems are signals defined on meshes, and a natural question is the extension of general scalar output regression models to such complex outputs. Changes between input geometries in terms of both size and adjacency structure in particular make this transition non-trivial. In this work, we propose an innovative strategy for Gaussian process regression where inputs are large and sparse graphs with continuous node attributes and outputs are signals defined on the nodes of the associated inputs. The methodology relies on the combination of regularized optimal transport, dimension reduction techniques, and the use of Gaussian processes indexed by graphs. In addition to enabling signal prediction, the main point of our proposal is to come with confidence intervals on node values, which is crucial for uncertainty quantification and active learning. Numerical experiments highlight the efficiency of the method to solve real problems in fluid dynamics and solid mechanics.

Gaussian process regression with Sliced Wasserstein Weisfeiler-Lehman graph kernels

Supervised learning has recently garnered significant attention in the field of computational physics due to its ability to effectively extract complex patterns for tasks like solving partial differential equations, or predicting material properties. Traditionally, such datasets consist of inputs given as meshes with a large number of nodes representing the problem geometry (seen as graphs), and corresponding outputs obtained with a numerical solver. This means the supervised learning model must be able to handle large and sparse graphs with continuous node attributes. In this work, we focus on Gaussian process regression, for which we introduce the Sliced Wasserstein Weisfeiler-Lehman (SWWL) graph kernel. In contrast to existing graph kernels, the proposed SWWL kernel enjoys positive definiteness and a drastic complexity reduction, which makes it possible to process datasets that were previously impossible to handle. The new kernel is first validated on graph classification for molecular datasets, where the input graphs have a few tens of nodes. The efficiency of the SWWL kernel is then illustrated on graph regression in computational fluid dynamics and solid mechanics, where the input graphs are made up of tens of thousands of nodes.

MMGP: a Mesh Morphing Gaussian Process-based machine learning method for regression of physical problems under non-parameterized geometrical variability

When learning simulations for modeling physical phenomena in industrial designs, geometrical variabilities are of prime interest. For parameterized geometries, classical regression techniques can be successfully employed. However, in practice, the shape parametrization is generally not available in the inference stage and we only have access to a mesh discretization. Learning mesh-based simulations is challenging and most of the recent advances have been relying on deep graph neural networks in order to overcome the limitations of standard machine learning approaches. While graph neural networks have shown promising performances, they still suffer from a few shortcomings, such as the need of large datasets or their inability to provide predictive uncertainties out of the shelf. In this work, we propose a machine learning method that do not rely on graph neural networks. Complex geometrical shapes and variations with fixed topology are dealt with using well-known mesh morphing onto a common support, combined with classical dimensionality reduction techniques and Gaussian processes. The proposed methodology can easily deal with large meshes, without knowing any parametrization describing the shape, and provide predictive uncertainties, which are of primary importance for decision-making. In the considered numerical experiments, the proposed method is competitive with respect to our implementation of graph neural networks, regarding either efficiency of the training and accuracy of the predictions.

Kernel Stein Discrepancy thinning: a theoretical perspective of pathologies and a practical fix with regularization

Stein thinning is a promising algorithm proposed by (Riabiz et al., 2022) for post-processing outputs of Markov chain Monte Carlo (MCMC). The main principle is to greedily minimize the kernelized Stein discrepancy (KSD), which only requires the gradient of the log-target distribution, and is thus well-suited for Bayesian inference. The main advantages of Stein thinning are the automatic remove of the burn-in period, the correction of the bias introduced by recent MCMC algorithms, and the asymptotic properties of convergence towards the target distribution. Nevertheless, Stein thinning suffers from several empirical pathologies, which may result in poor approximations, as observed in the literature. In this article, we conduct a theoretical analysis of these pathologies, to clearly identify the mechanisms at stake, and suggest improved strategies. Then, we introduce the regularized Stein thinning algorithm to alleviate the identified pathologies. Finally, theoretical guarantees and extensive experiments show the high efficiency of the proposed algorithm.

Quantitative performance evaluation of Bayesian neural networks

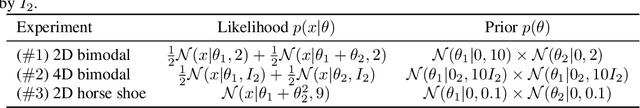
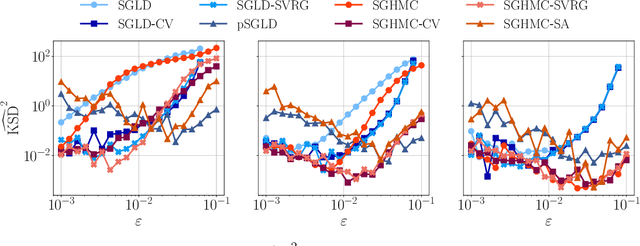
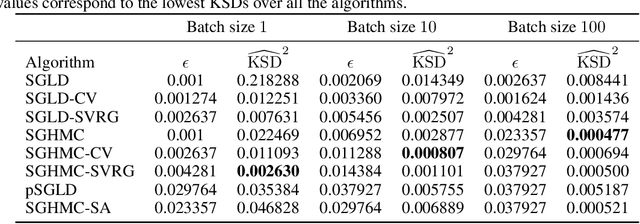
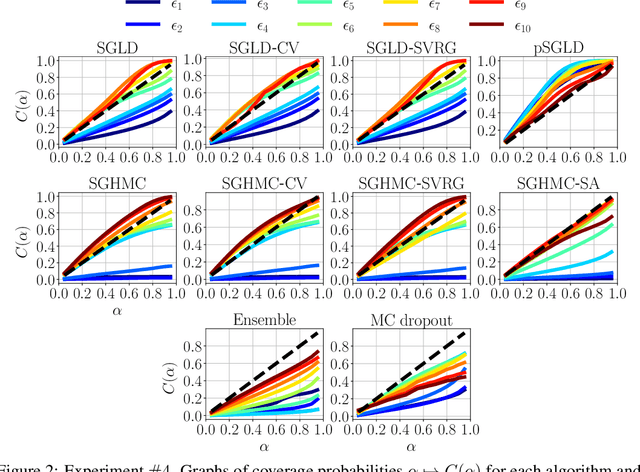
Due to the growing adoption of deep neural networks in many fields of science and engineering, modeling and estimating their uncertainties has become of primary importance. Various approaches have been investigated including Bayesian neural networks, ensembles, deterministic approximations, amongst others. Despite the growing litterature about uncertainty quantification in deep learning, the quality of the uncertainty estimates remains an open question. In this work, we attempt to assess the performance of several algorithms on sampling and regression tasks by evaluating the quality of the confidence regions and how well the generated samples are representative of the unknown target distribution. Towards this end, several sampling and regression tasks are considered, and the selected algorithms are compared in terms of coverage probabilities, kernelized Stein discrepancies, and maximum mean discrepancies.