Transformers Learn Shortcuts to Automata

Algorithmic reasoning requires capabilities which are most naturally understood through recurrent models of computation, like the Turing machine. However, Transformer models, while lacking recurrence, are able to perform such reasoning using far fewer layers than the number of reasoning steps. This raises the question: what solutions are these shallow and non-recurrent models finding? We investigate this question in the setting of learning automata, discrete dynamical systems naturally suited to recurrent modeling and expressing algorithmic tasks. Our theoretical results completely characterize shortcut solutions, whereby a shallow Transformer with only $o(T)$ layers can exactly replicate the computation of an automaton on an input sequence of length $T$. By representing automata using the algebraic structure of their underlying transformation semigroups, we obtain $O(\log T)$-depth simulators for all automata and $O(1)$-depth simulators for all automata whose associated groups are solvable. Empirically, we perform synthetic experiments by training Transformers to simulate a wide variety of automata, and show that shortcut solutions can be learned via standard training. We further investigate the brittleness of these solutions and propose potential mitigations.

Anti-Concentrated Confidence Bonuses for Scalable Exploration

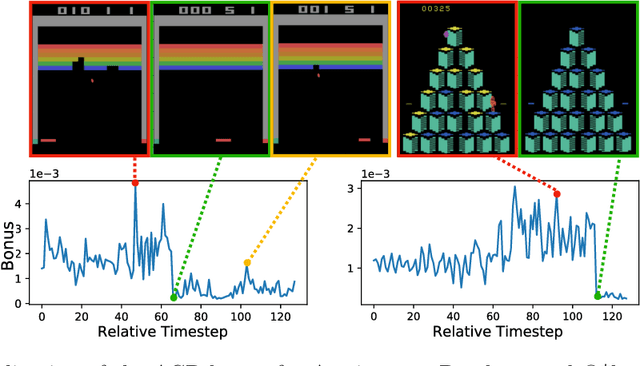
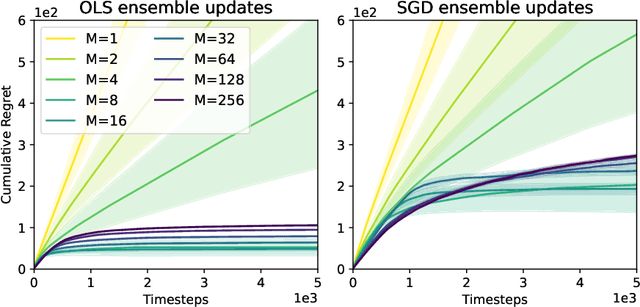
Intrinsic rewards play a central role in handling the exploration-exploitation trade-off when designing sequential decision-making algorithms, in both foundational theory and state-of-the-art deep reinforcement learning. The LinUCB algorithm, a centerpiece of the stochastic linear bandits literature, prescribes an elliptical bonus which addresses the challenge of leveraging shared information in large action spaces. This bonus scheme cannot be directly transferred to high-dimensional exploration problems, however, due to the computational cost of maintaining the inverse covariance matrix of action features. We introduce \emph{anti-concentrated confidence bounds} for efficiently approximating the elliptical bonus, using an ensemble of regressors trained to predict random noise from policy network-derived features. Using this approximation, we obtain stochastic linear bandit algorithms which obtain $\tilde O(d \sqrt{T})$ regret bounds for $\mathrm{poly}(d)$ fixed actions. We develop a practical variant for deep reinforcement learning that is competitive with contemporary intrinsic reward heuristics on Atari benchmarks.

Investigating the Role of Negatives in Contrastive Representation Learning

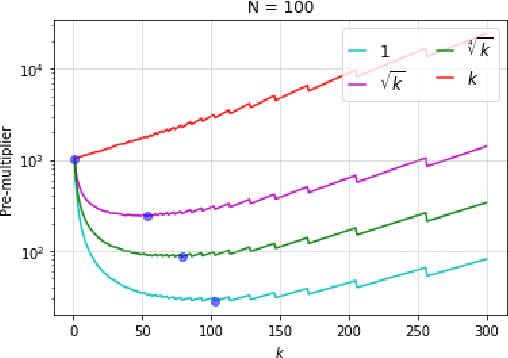
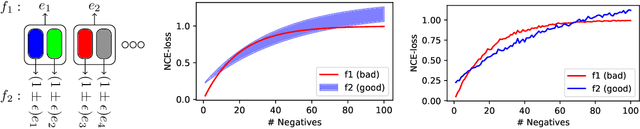
Noise contrastive learning is a popular technique for unsupervised representation learning. In this approach, a representation is obtained via reduction to supervised learning, where given a notion of semantic similarity, the learner tries to distinguish a similar (positive) example from a collection of random (negative) examples. The success of modern contrastive learning pipelines relies on many parameters such as the choice of data augmentation, the number of negative examples, and the batch size; however, there is limited understanding as to how these parameters interact and affect downstream performance. We focus on disambiguating the role of one of these parameters: the number of negative examples. Theoretically, we show the existence of a collision-coverage trade-off suggesting that the optimal number of negative examples should scale with the number of underlying concepts in the data. Empirically, we scrutinize the role of the number of negatives in both NLP and vision tasks. In the NLP task, we find that the results broadly agree with our theory, while our vision experiments are murkier with performance sometimes even being insensitive to the number of negatives. We discuss plausible explanations for this behavior and suggest future directions to better align theory and practice.

Gone Fishing: Neural Active Learning with Fisher Embeddings

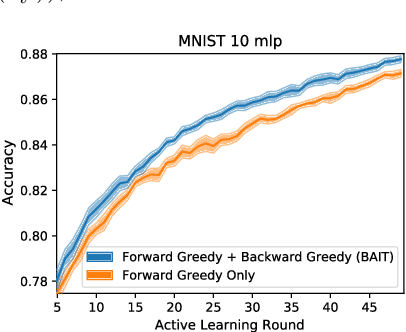
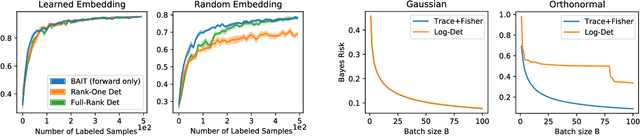
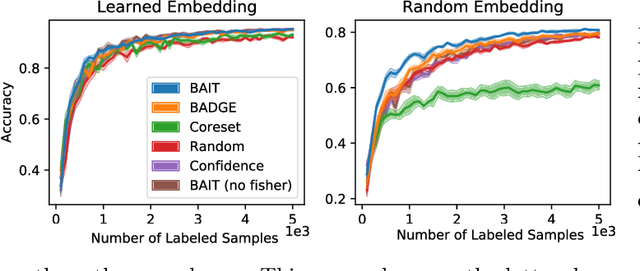
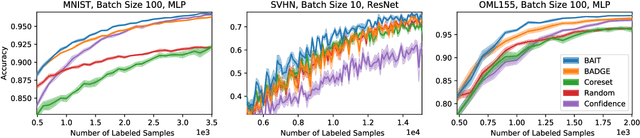
There is an increasing need for effective active learning algorithms that are compatible with deep neural networks. While there are many classic, well-studied sample selection methods, the non-convexity and varying internal representation of neural models make it unclear how to extend these approaches. This article introduces BAIT, a practical, tractable, and high-performing active learning algorithm for neural networks that addresses these concerns. BAIT draws inspiration from the theoretical analysis of maximum likelihood estimators (MLE) for parametric models. It selects batches of samples by optimizing a bound on the MLE error in terms of the Fisher information, which we show can be implemented efficiently at scale by exploiting linear-algebraic structure especially amenable to execution on modern hardware. Our experiments show that BAIT outperforms the previous state of the art on both classification and regression problems, and is flexible enough to be used with a variety of model architectures.

Learning Composable Energy Surrogates for PDE Order Reduction

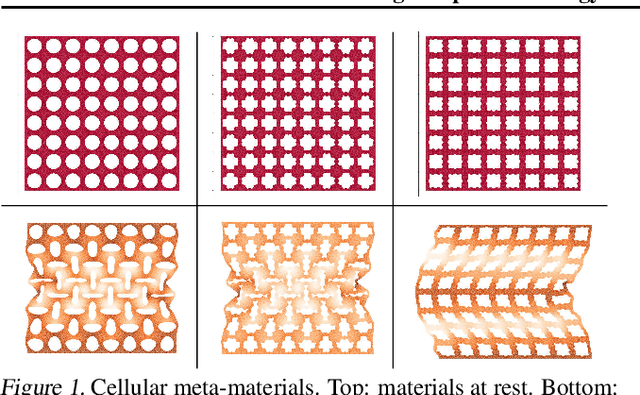
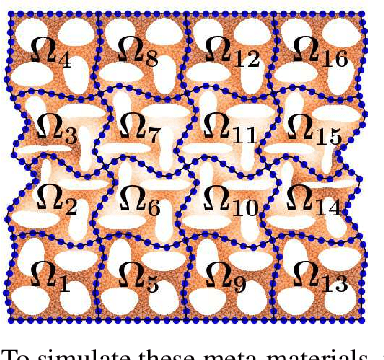
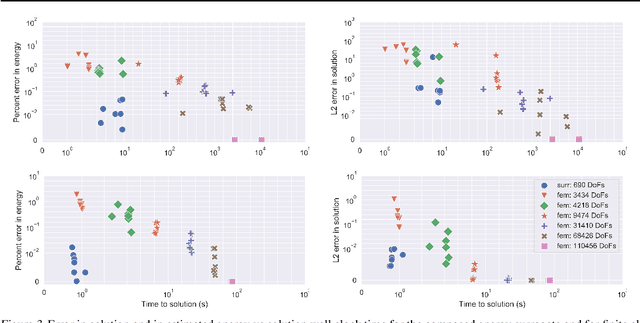
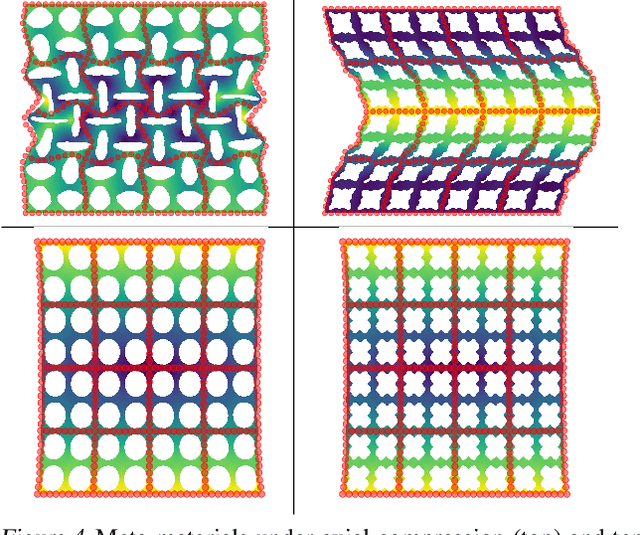
Meta-materials are an important emerging class of engineered materials in which complex macroscopic behaviour--whether electromagnetic, thermal, or mechanical--arises from modular substructure. Simulation and optimization of these materials are computationally challenging, as rich substructures necessitate high-fidelity finite element meshes to solve the governing PDEs. To address this, we leverage parametric modular structure to learn component-level surrogates, enabling cheaper high-fidelity simulation. We use a neural network to model the stored potential energy in a component given boundary conditions. This yields a structured prediction task: macroscopic behavior is determined by the minimizer of the system's total potential energy, which can be approximated by composing these surrogate models. Composable energy surrogates thus permit simulation in the reduced basis of component boundaries. Costly ground-truth simulation of the full structure is avoided, as training data are generated by performing finite element analysis with individual components. Using dataset aggregation to choose training boundary conditions allows us to learn energy surrogates which produce accurate macroscopic behavior when composed, accelerating simulation of parametric meta-materials.

On the Difficulty of Warm-Starting Neural Network Training

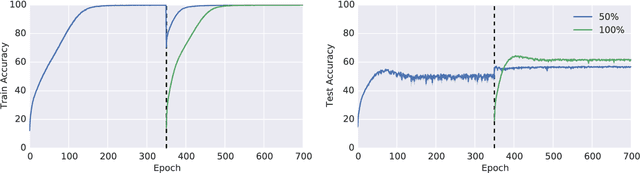
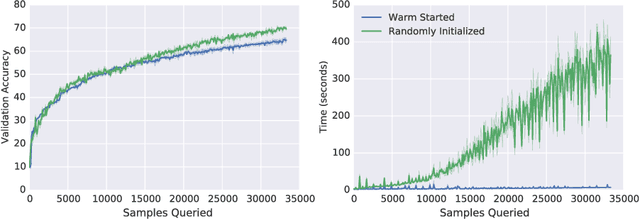
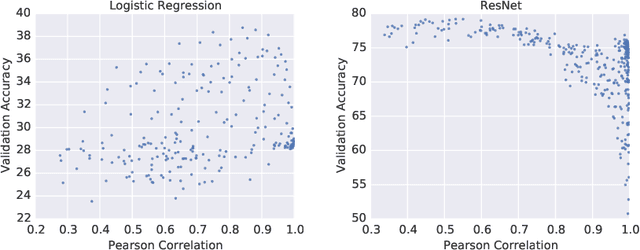
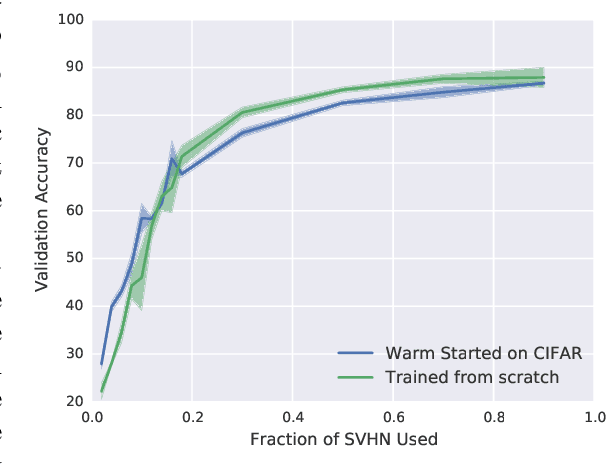
In many real-world deployments of machine learning systems, data arrive piecemeal. These learning scenarios may be passive, where data arrive incrementally due to structural properties of the problem (e.g., daily financial data) or active, where samples are selected according to a measure of their quality (e.g., experimental design). In both of these cases, we are building a sequence of models that incorporate an increasing amount of data. We would like each of these models in the sequence to be performant and take advantage of all the data that are available to that point. Conventional intuition suggests that when solving a sequence of related optimization problems of this form, it should be possible to initialize using the solution of the previous iterate---to "warm start" the optimization rather than initialize from scratch---and see reductions in wall-clock time. However, in practice this warm-starting seems to yield poorer generalization performance than models that have fresh random initializations, even though the final training losses are similar. While it appears that some hyperparameter settings allow a practitioner to close this generalization gap, they seem to only do so in regimes that damage the wall-clock gains of the warm start. Nevertheless, it is highly desirable to be able to warm-start neural network training, as it would dramatically reduce the resource usage associated with the construction of performant deep learning systems. In this work, we take a closer look at this empirical phenomenon and try to understand when and how it occurs. Although the present investigation did not lead to a solution, we hope that a thorough articulation of the problem will spur new research that may lead to improved methods that consume fewer resources during training.

Deep Batch Active Learning by Diverse, Uncertain Gradient Lower Bounds

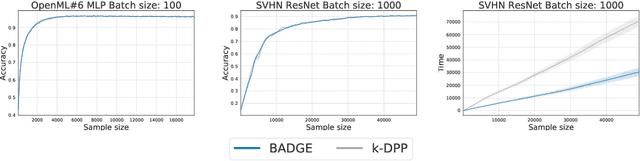
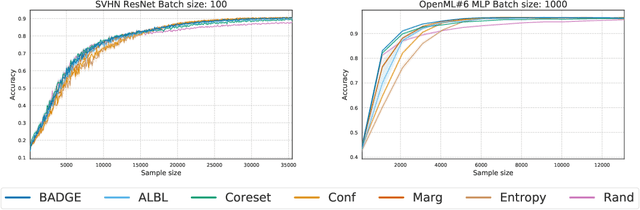
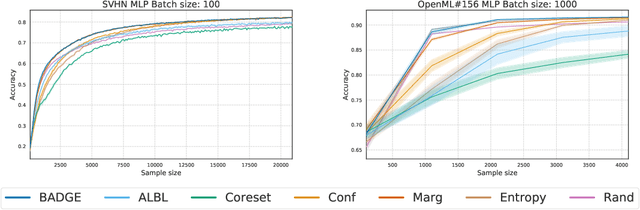
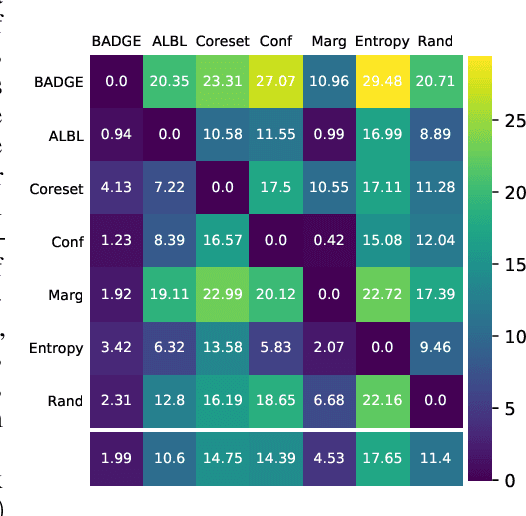
We design a new algorithm for batch active learning with deep neural network models. Our algorithm, Batch Active learning by Diverse Gradient Embeddings (BADGE), samples groups of points that are disparate and high-magnitude when represented in a hallucinated gradient space, a strategy designed to incorporate both predictive uncertainty and sample diversity into every selected batch. Crucially, BADGE trades off between diversity and uncertainty without requiring any hand-tuned hyperparameters. We show that while other approaches sometimes succeed for particular batch sizes or architectures, BADGE consistently performs as well or better, making it a versatile option for practical active learning problems.

Unsupervised Domain Adaptation Using Approximate Label Matching

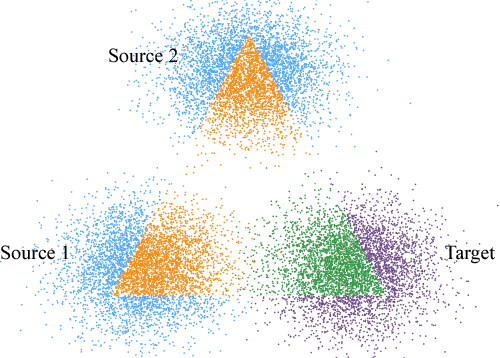
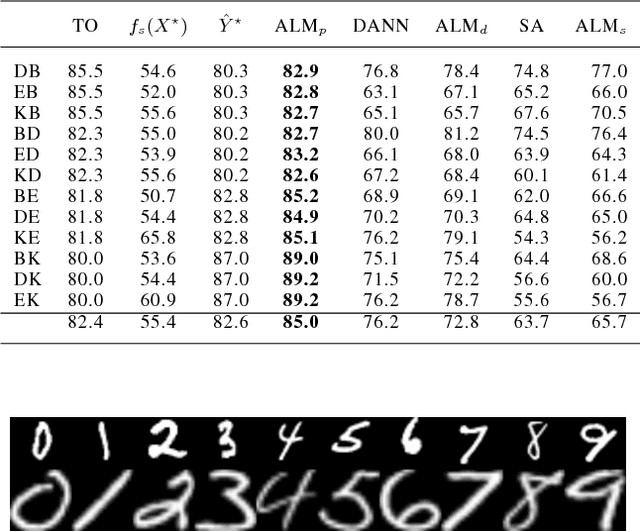
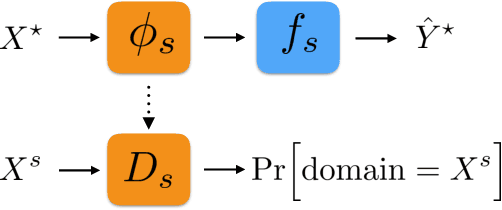
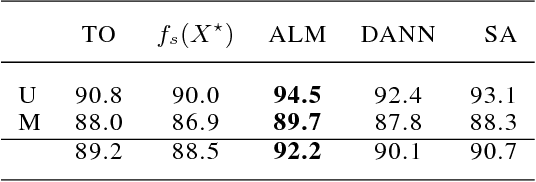
Domain adaptation addresses the problem created when training data is generated by a so-called source distribution, but test data is generated by a significantly different target distribution. In this work, we present approximate label matching (ALM), a new unsupervised domain adaptation technique that creates and leverages a rough labeling on the test samples, then uses these noisy labels to learn a transformation that aligns the source and target samples. We show that the transformation estimated by ALM has favorable properties compared to transformations estimated by other methods, which do not use any kind of target labeling. Our model is regularized by requiring that a classifier trained to discriminate source from transformed target samples cannot distinguish between the two. We experiment with ALM on simulated and real data, and show that it outperforms techniques commonly used in the field.