Nonlinear Kalman Filtering with Reparametrization Gradients

We introduce a novel nonlinear Kalman filter that utilizes reparametrization gradients. The widely used parametric approximation is based on a jointly Gaussian assumption of the state-space model, which is in turn equivalent to minimizing an approximation to the Kullback-Leibler divergence. It is possible to obtain better approximations using the alpha divergence, but the resulting problem is substantially more complex. In this paper, we introduce an alternate formulation based on an energy function, which can be optimized instead of the alpha divergence. The optimization can be carried out using reparametrization gradients, a technique that has recently been utilized in a number of deep learning models.

Self-Verification in Image Denoising

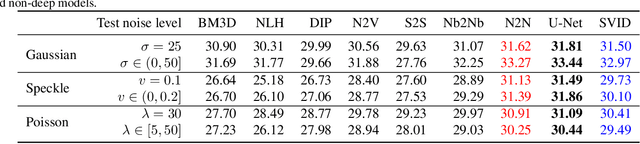
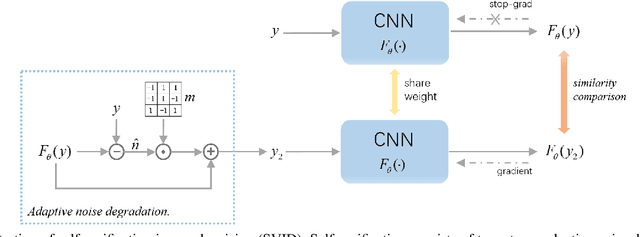
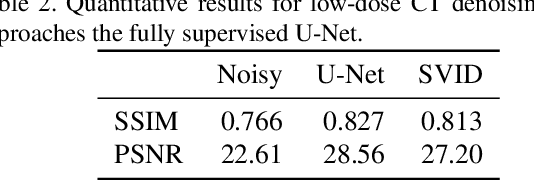
We devise a new regularization, called self-verification, for image denoising. This regularization is formulated using a deep image prior learned by the network, rather than a traditional predefined prior. Specifically, we treat the output of the network as a ``prior'' that we denoise again after ``re-noising''. The comparison between the again denoised image and its prior can be interpreted as a self-verification of the network's denoising ability. We demonstrate that self-verification encourages the network to capture low-level image statistics needed to restore the image. Based on this self-verification regularization, we further show that the network can learn to denoise even if it has not seen any clean images. This learning strategy is self-supervised, and we refer to it as Self-Verification Image Denoising (SVID). SVID can be seen as a mixture of learning-based methods and traditional model-based denoising methods, in which regularization is adaptively formulated using the output of the network. We show the application of SVID to various denoising tasks using only observed corrupted data. It can achieve the denoising performance close to supervised CNNs.

Bayesian non-parametric non-negative matrix factorization for pattern identification in environmental mixtures

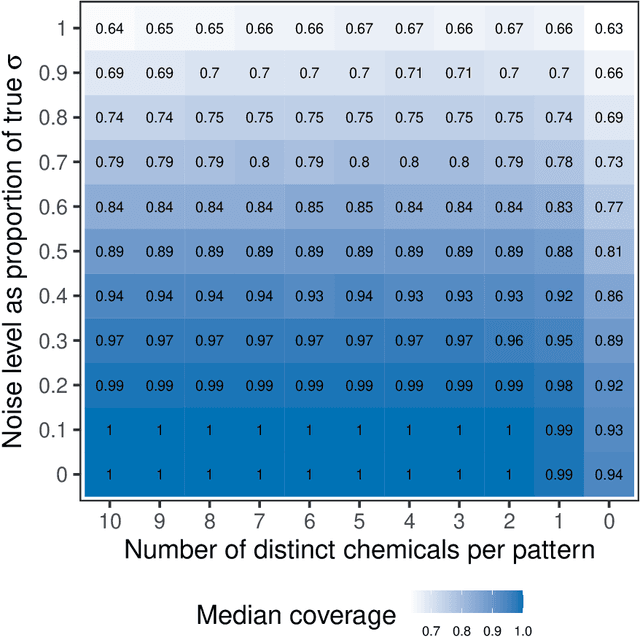
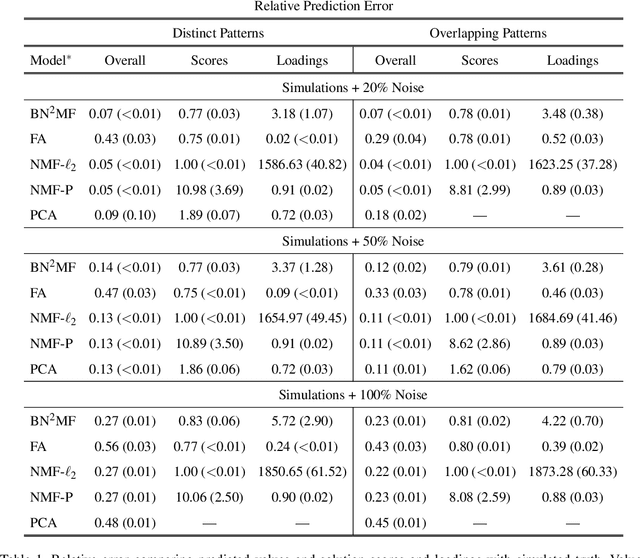
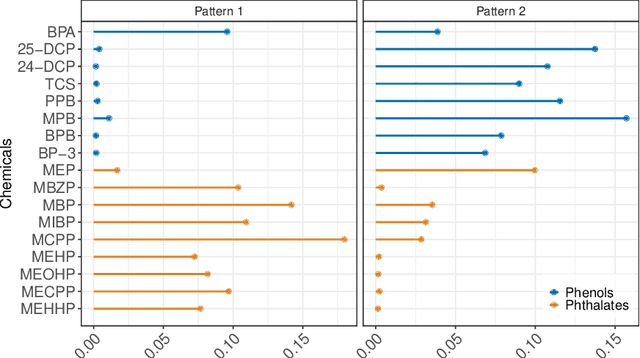
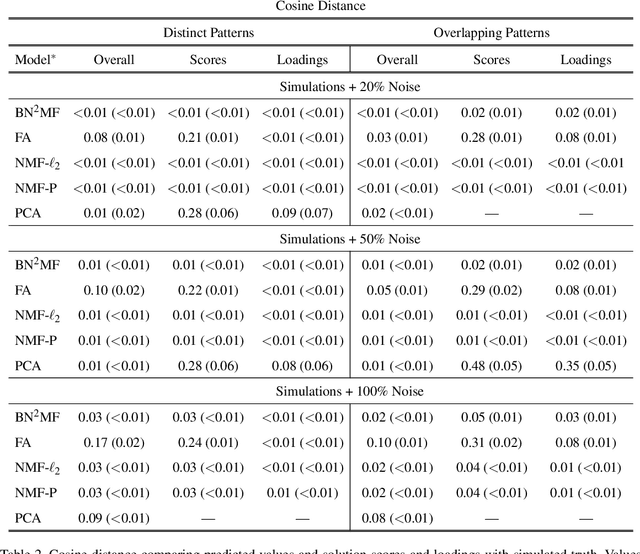
Environmental health researchers may aim to identify exposure patterns that represent sources, product use, or behaviors that give rise to mixtures of potentially harmful environmental chemical exposures. We present Bayesian non-parametric non-negative matrix factorization (BN^2MF) as a novel method to identify patterns of chemical exposures when the number of patterns is not known a priori. We placed non-negative continuous priors on pattern loadings and individual scores to enhance interpretability and used a clever non-parametric sparse prior to estimate the pattern number. We further derived variational confidence intervals around estimates; this is a critical development because it quantifies the model's confidence in estimated patterns. These unique features contrast with existing pattern recognition methods employed in this field which are limited by user-specified pattern number, lack of interpretability of patterns in terms of human understanding, and lack of uncertainty quantification.

Adaptive noise imitation for image denoising

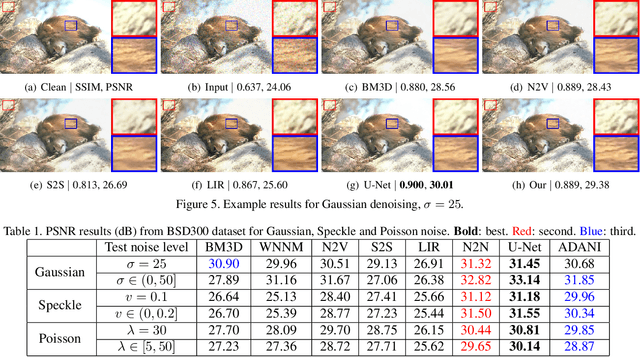
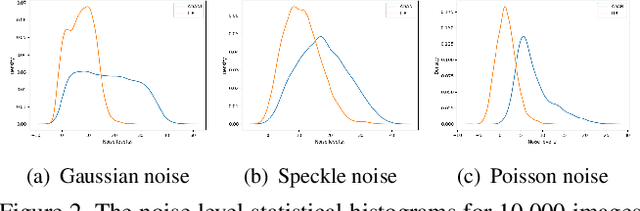
The effectiveness of existing denoising algorithms typically relies on accurate pre-defined noise statistics or plenty of paired data, which limits their practicality. In this work, we focus on denoising in the more common case where noise statistics and paired data are unavailable. Considering that denoising CNNs require supervision, we develop a new \textbf{adaptive noise imitation (ADANI)} algorithm that can synthesize noisy data from naturally noisy images. To produce realistic noise, a noise generator takes unpaired noisy/clean images as input, where the noisy image is a guide for noise generation. By imposing explicit constraints on the type, level and gradient of noise, the output noise of ADANI will be similar to the guided noise, while keeping the original clean background of the image. Coupling the noisy data output from ADANI with the corresponding ground-truth, a denoising CNN is then trained in a fully-supervised manner. Experiments show that the noisy data produced by ADANI are visually and statistically similar to real ones so that the denoising CNN in our method is competitive to other networks trained with external paired data.

Bayesian recurrent state space model for rs-fMRI

We propose a hierarchical Bayesian recurrent state space model for modeling switching network connectivity in resting state fMRI data. Our model allows us to uncover shared network patterns across disease conditions. We evaluate our method on the ADNI2 dataset by inferring latent state patterns corresponding to altered neural circuits in individuals with Mild Cognitive Impairment (MCI). In addition to states shared across healthy and individuals with MCI, we discover latent states that are predominantly observed in individuals with MCI. Our model outperforms current state of the art deep learning method on ADNI2 dataset.

Deep Bayesian Nonparametric Factor Analysis

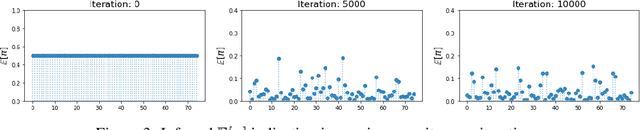
We propose a deep generative factor analysis model with beta process prior that can approximate complex non-factorial distributions over the latent codes. We outline a stochastic EM algorithm for scalable inference in a specific instantiation of this model and present some preliminary results.

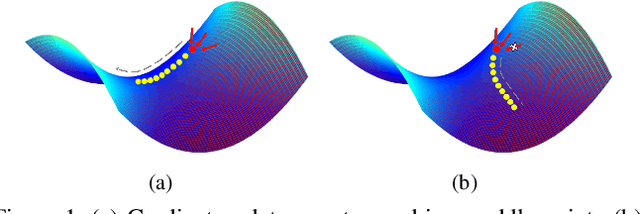
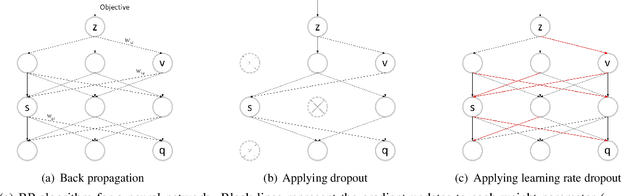
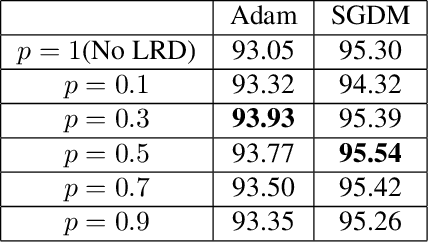
Learning Rate Dropout

The performance of a deep neural network is highly dependent on its training, and finding better local optimal solutions is the goal of many optimization algorithms. However, existing optimization algorithms show a preference for descent paths that converge slowly and do not seek to avoid bad local optima. In this work, we propose Learning Rate Dropout (LRD), a simple gradient descent technique for training related to coordinate descent. LRD empirically aids the optimizer to actively explore in the parameter space by randomly setting some learning rates to zero; at each iteration, only parameters whose learning rate is not 0 are updated. As the learning rate of different parameters is dropped, the optimizer will sample a new loss descent path for the current update. The uncertainty of the descent path helps the model avoid saddle points and bad local minima. Experiments show that LRD is surprisingly effective in accelerating training while preventing overfitting.

Noise2Blur: Online Noise Extraction and Denoising

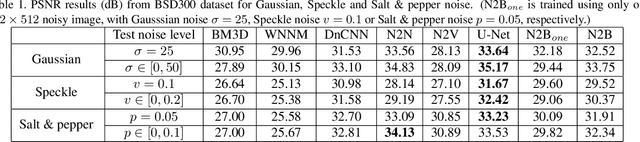
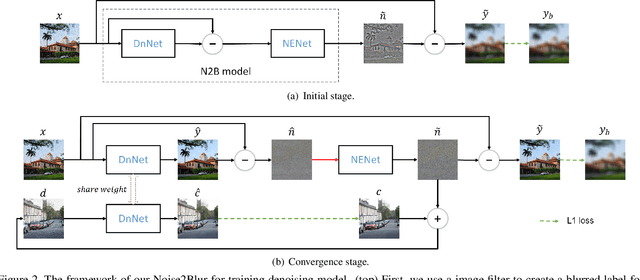
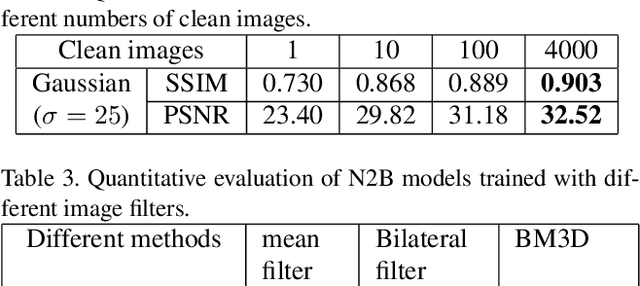
We propose a new framework called Noise2Blur (N2B) for training robust image denoising models without pre-collected paired noisy/clean images. The training of the model requires only some (or even one) noisy images, some random unpaired clean images, and noise-free but blurred labels obtained by predefined filtering of the noisy images. The N2B model consists of two parts: a denoising network and a noise extraction network. First, the noise extraction network learns to output a noise map using the noise information from the denoising network under the guidence of the blurred labels. Then, the noise map is added to a clean image to generate a new ``noisy/clean'' image pair. Using the new image pair, the denoising network learns to generate clean and high-quality images from noisy observations. These two networks are trained simultaneously and mutually aid each other to learn the mappings of noise to clean/blur. Experiments on several denoising tasks show that the denoising performance of N2B is close to that of other denoising CNNs trained with pre-collected paired data.

Risk Bounds for Low Cost Bipartite Ranking

Bipartite ranking is an important supervised learning problem; however, unlike regression or classification, it has a quadratic dependence on the number of samples. To circumvent the prohibitive sample cost, many recent work focus on stochastic gradient-based methods. In this paper we consider an alternative approach, which leverages the structure of the widely-adopted pairwise squared loss, to obtain a stochastic and low cost algorithm that does not require stochastic gradients or learning rates. Using a novel uniform risk bound---based on matrix and vector concentration inequalities---we show that the sample size required for competitive performance against the all-pairs batch algorithm does not have a quadratic dependence. Generalization bounds for both the batch and low cost stochastic algorithms are presented. Experimental results show significant speed gain against the batch algorithm, as well as competitive performance against state-of-the-art bipartite ranking algorithms on real datasets.

Accurate Uncertainty Estimation and Decomposition in Ensemble Learning

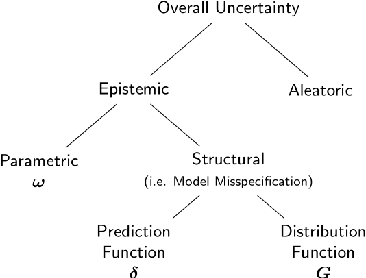
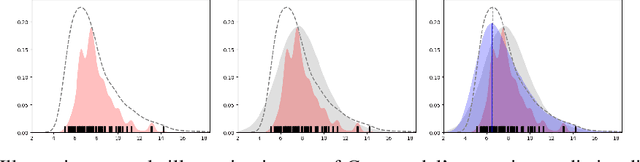
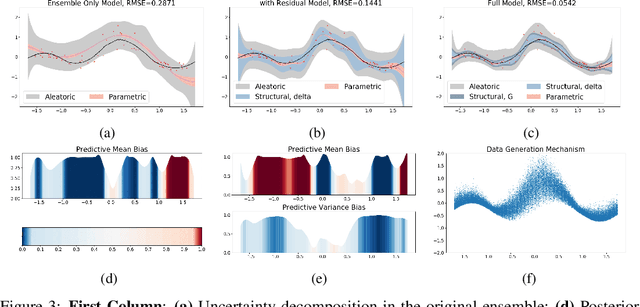
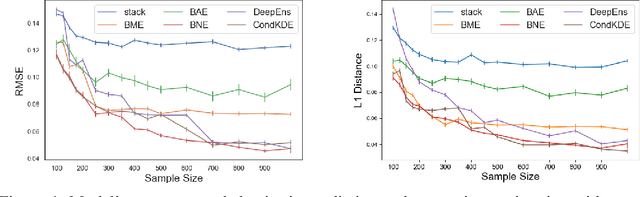
Ensemble learning is a standard approach to building machine learning systems that capture complex phenomena in real-world data. An important aspect of these systems is the complete and valid quantification of model uncertainty. We introduce a Bayesian nonparametric ensemble (BNE) approach that augments an existing ensemble model to account for different sources of model uncertainty. BNE augments a model's prediction and distribution functions using Bayesian nonparametric machinery. It has a theoretical guarantee in that it robustly estimates the uncertainty patterns in the data distribution, and can decompose its overall predictive uncertainty into distinct components that are due to different sources of noise and error. We show that our method achieves accurate uncertainty estimates under complex observational noise, and illustrate its real-world utility in terms of uncertainty decomposition and model bias detection for an ensemble in predict air pollution exposures in Eastern Massachusetts, USA.