Robust testing of low-dimensional functions

A natural problem in high-dimensional inference is to decide if a classifier $f:\mathbb{R}^n \rightarrow [-1,1]$ depends on a small number of linear directions of its input data. Call a function $g: \mathbb{R}^n \rightarrow [-1,1]$, a linear $k$-junta if it is completely determined by some $k$-dimensional subspace of the input space. A recent work of the authors showed that linear $k$-juntas are testable. Thus there exists an algorithm to distinguish between: 1. $f: \mathbb{R}^n \rightarrow \{-1,1\}$ which is a linear $k$-junta with surface area $s$, 2. $f$ is $\epsilon$-far from any linear $k$-junta, where the query complexity of the algorithm is independent of the ambient dimension $n$. Following the surge of interest in noise-tolerant property testing, in this paper we prove a noise-tolerant (or robust) version of this result. Namely, we give an algorithm which given any $c>0$, $\epsilon>0$, distinguishes between 1. $f: \mathbb{R}^n \rightarrow \{-1,1\}$ has correlation at least $c$ with some linear $k$-junta with surface area $s$. 2. $f$ has correlation at most $c-\epsilon$ with any linear $k$-junta. Our query complexity is qualitatively the same, i.e., remains independent of $n$ and is polynomially dependent on $k$. A major motivation for studying Linear Junta Testing come from statistical models where it is crucial to allow noise. In the language of model compression, our results show statistical models can be "compressed" in query complexity that depends only on the size of the desired compression, when the compression is a linear Junta.

The Search Problem in Mixture Models

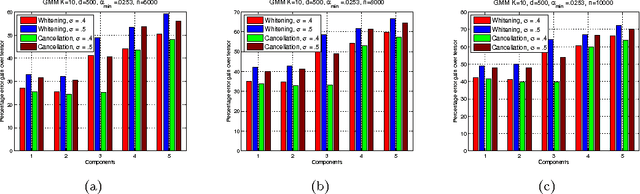
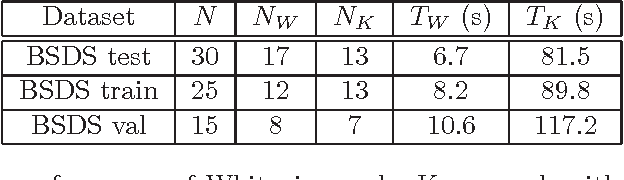
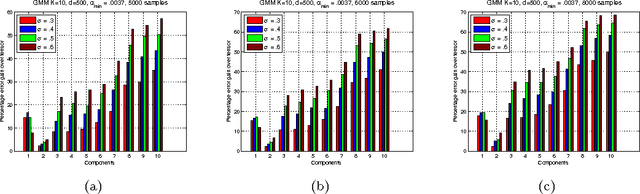
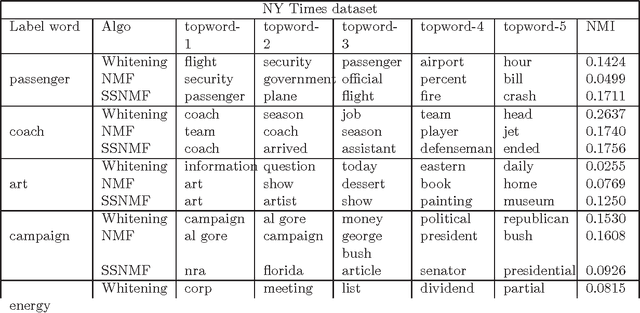
We consider the task of learning the parameters of a {\em single} component of a mixture model, for the case when we are given {\em side information} about that component, we call this the "search problem" in mixture models. We would like to solve this with computational and sample complexity lower than solving the overall original problem, where one learns parameters of all components. Our main contributions are the development of a simple but general model for the notion of side information, and a corresponding simple matrix-based algorithm for solving the search problem in this general setting. We then specialize this model and algorithm to four common scenarios: Gaussian mixture models, LDA topic models, subspace clustering, and mixed linear regression. For each one of these we show that if (and only if) the side information is informative, we obtain parameter estimates with greater accuracy, and also improved computation complexity than existing moment based mixture model algorithms (e.g. tensor methods). We also illustrate several natural ways one can obtain such side information, for specific problem instances. Our experiments on real data sets (NY Times, Yelp, BSDS500) further demonstrate the practicality of our algorithms showing significant improvement in runtime and accuracy.

Preference Completion: Large-scale Collaborative Ranking from Pairwise Comparisons

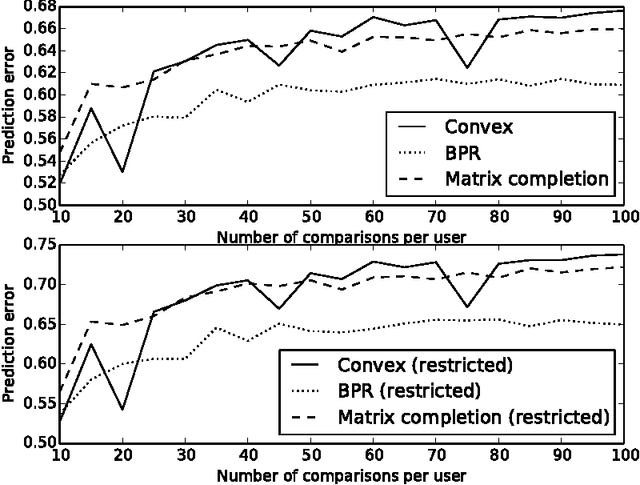
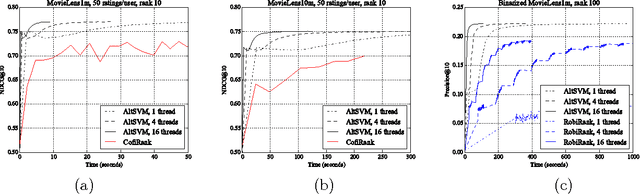
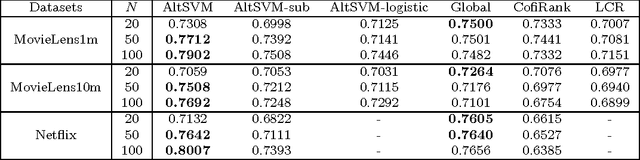
In this paper we consider the collaborative ranking setting: a pool of users each provides a small number of pairwise preferences between $d$ possible items; from these we need to predict preferences of the users for items they have not yet seen. We do so by fitting a rank $r$ score matrix to the pairwise data, and provide two main contributions: (a) we show that an algorithm based on convex optimization provides good generalization guarantees once each user provides as few as $O(r\log^2 d)$ pairwise comparisons -- essentially matching the sample complexity required in the related matrix completion setting (which uses actual numerical as opposed to pairwise information), and (b) we develop a large-scale non-convex implementation, which we call AltSVM, that trains a factored form of the matrix via alternating minimization (which we show reduces to alternating SVM problems), and scales and parallelizes very well to large problem settings. It also outperforms common baselines on many moderately large popular collaborative filtering datasets in both NDCG and in other measures of ranking performance.

Spectral redemption: clustering sparse networks

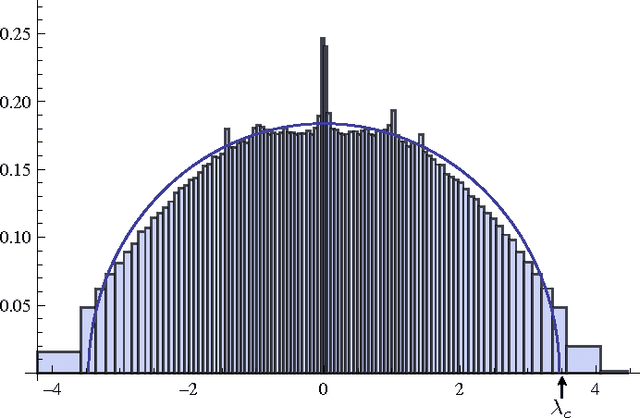
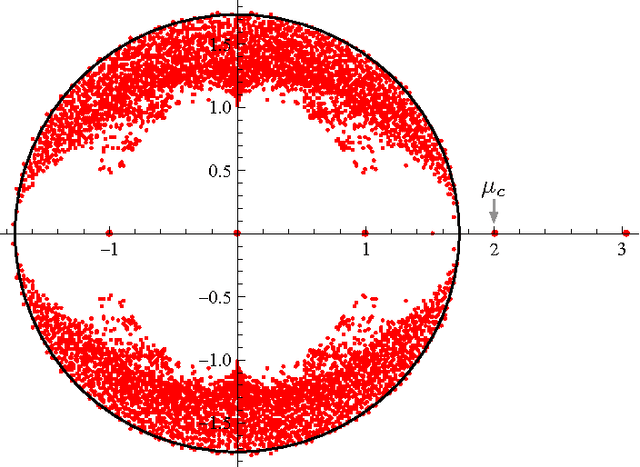
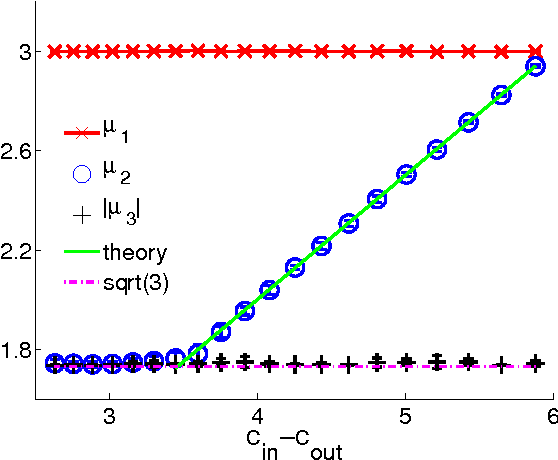
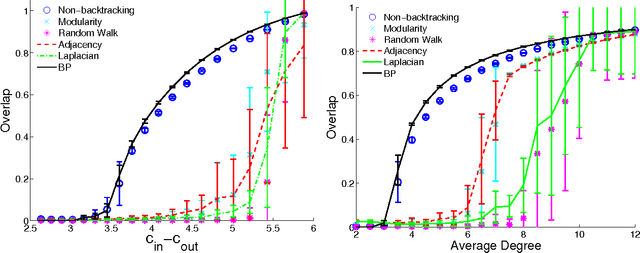
Spectral algorithms are classic approaches to clustering and community detection in networks. However, for sparse networks the standard versions of these algorithms are suboptimal, in some cases completely failing to detect communities even when other algorithms such as belief propagation can do so. Here we introduce a new class of spectral algorithms based on a non-backtracking walk on the directed edges of the graph. The spectrum of this operator is much better-behaved than that of the adjacency matrix or other commonly used matrices, maintaining a strong separation between the bulk eigenvalues and the eigenvalues relevant to community structure even in the sparse case. We show that our algorithm is optimal for graphs generated by the stochastic block model, detecting communities all the way down to the theoretical limit. We also show the spectrum of the non-backtracking operator for some real-world networks, illustrating its advantages over traditional spectral clustering.