Binary perceptron: efficient algorithms can find solutions in a rare well-connected cluster

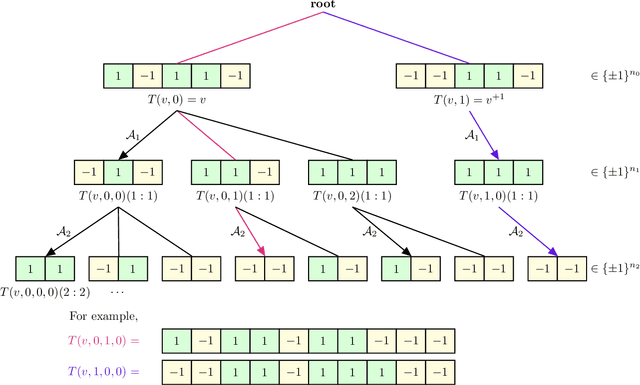
It was recently shown that almost all solutions in the symmetric binary perceptron are isolated, even at low constraint densities, suggesting that finding typical solutions is hard. In contrast, some algorithms have been shown empirically to succeed in finding solutions at low density. This phenomenon has been justified numerically by the existence of subdominant and dense connected regions of solutions, which are accessible by simple learning algorithms. In this paper, we establish formally such a phenomenon for both the symmetric and asymmetric binary perceptrons. We show that at low constraint density (equivalently for overparametrized perceptrons), there exists indeed a subdominant connected cluster of solutions with almost maximal diameter, and that an efficient multiscale majority algorithm can find solutions in such a cluster with high probability, settling in particular an open problem posed by Perkins-Xu '21. In addition, even close to the critical threshold, we show that there exist clusters of linear diameter for the symmetric perceptron, as well as for the asymmetric perceptron under additional assumptions.

Proof of the Contiguity Conjecture and Lognormal Limit for the Symmetric Perceptron

We consider the symmetric binary perceptron model, a simple model of neural networks that has gathered significant attention in the statistical physics, information theory and probability theory communities, with recent connections made to the performance of learning algorithms in Baldassi et al. '15. We establish that the partition function of this model, normalized by its expected value, converges to a lognormal distribution. As a consequence, this allows us to establish several conjectures for this model: (i) it proves the contiguity conjecture of Aubin et al. '19 between the planted and unplanted models in the satisfiable regime; (ii) it establishes the sharp threshold conjecture; (iii) it proves the frozen 1-RSB conjecture in the symmetric case, conjectured first by Krauth-M\'ezard '89 in the asymmetric case. In a recent concurrent work of Perkins-Xu [PX21], the last two conjectures were also established by proving that the partition function concentrates on an exponential scale. This left open the contiguity conjecture and the lognormal limit characterization, which are established here. In particular, our proof technique relies on a dense counter-part of the small graph conditioning method, which was developed for sparse models in the celebrated work of Robinson and Wormald.

Learning Sparse Graphons and the Generalized Kesten-Stigum Threshold

The problem of learning graphons has attracted considerable attention across several scientific communities, with significant progress over the recent years in sparser regimes. Yet, the current techniques still require diverging degrees in order to succeed with efficient algorithms in the challenging cases where the local structure of the graph is homogeneous. This paper provides an efficient algorithm to learn graphons in the constant expected degree regime. The algorithm is shown to succeed in estimating the rank-$k$ projection of a graphon in the $L_2$ metric if the top $k$ eigenvalues of the graphon satisfy a generalized Kesten-Stigum condition.

Spectral redemption: clustering sparse networks

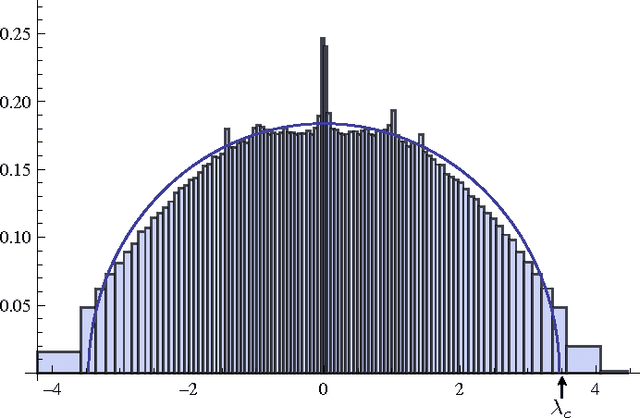
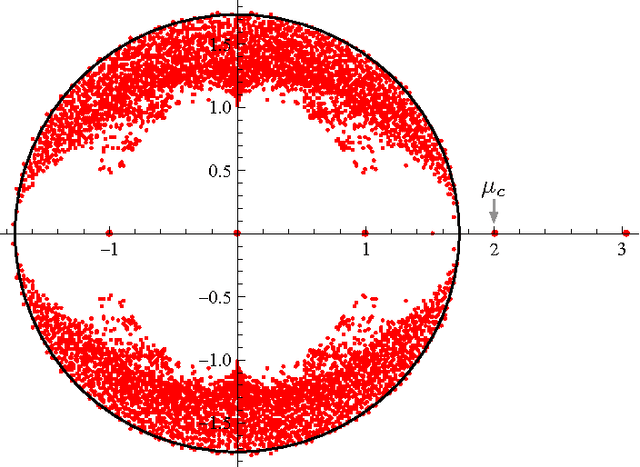
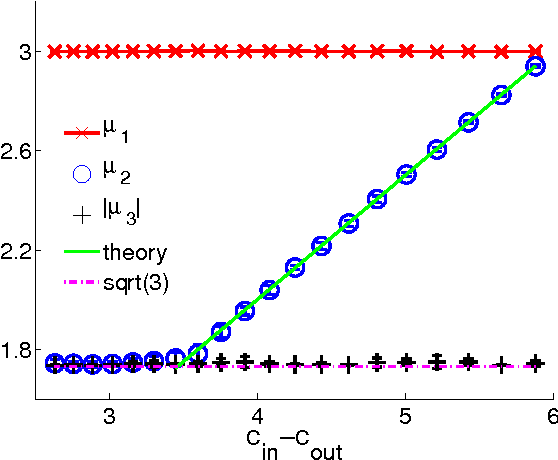
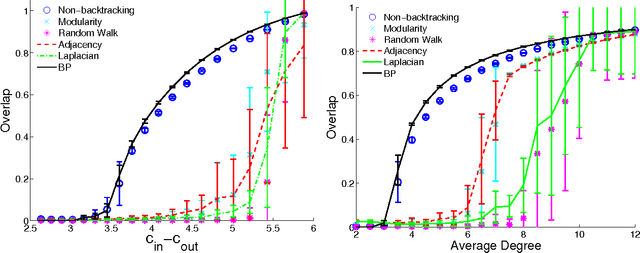
Spectral algorithms are classic approaches to clustering and community detection in networks. However, for sparse networks the standard versions of these algorithms are suboptimal, in some cases completely failing to detect communities even when other algorithms such as belief propagation can do so. Here we introduce a new class of spectral algorithms based on a non-backtracking walk on the directed edges of the graph. The spectrum of this operator is much better-behaved than that of the adjacency matrix or other commonly used matrices, maintaining a strong separation between the bulk eigenvalues and the eigenvalues relevant to community structure even in the sparse case. We show that our algorithm is optimal for graphs generated by the stochastic block model, detecting communities all the way down to the theoretical limit. We also show the spectrum of the non-backtracking operator for some real-world networks, illustrating its advantages over traditional spectral clustering.

Robust estimation of latent tree graphical models: Inferring hidden states with inexact parameters

Latent tree graphical models are widely used in computational biology, signal and image processing, and network tomography. Here we design a new efficient, estimation procedure for latent tree models, including Gaussian and discrete, reversible models, that significantly improves on previous sample requirement bounds. Our techniques are based on a new hidden state estimator which is robust to inaccuracies in estimated parameters. More precisely, we prove that latent tree models can be estimated with high probability in the so-called Kesten-Stigum regime with $O(log^2 n)$ samples where $n$ is the number of nodes.

Reconstruction of Markov Random Fields from Samples: Some Easy Observations and Algorithms

Markov random fields are used to model high dimensional distributions in a number of applied areas. Much recent interest has been devoted to the reconstruction of the dependency structure from independent samples from the Markov random fields. We analyze a simple algorithm for reconstructing the underlying graph defining a Markov random field on $n$ nodes and maximum degree $d$ given observations. We show that under mild non-degeneracy conditions it reconstructs the generating graph with high probability using $\Theta(d \epsilon^{-2}\delta^{-4} \log n)$ samples where $\epsilon,\delta$ depend on the local interactions. For most local interaction $\eps,\delta$ are of order $\exp(-O(d))$. Our results are optimal as a function of $n$ up to a multiplicative constant depending on $d$ and the strength of the local interactions. Our results seem to be the first results for general models that guarantee that {\em the} generating model is reconstructed. Furthermore, we provide explicit $O(n^{d+2} \epsilon^{-2}\delta^{-4} \log n)$ running time bound. In cases where the measure on the graph has correlation decay, the running time is $O(n^2 \log n)$ for all fixed $d$. We also discuss the effect of observing noisy samples and show that as long as the noise level is low, our algorithm is effective. On the other hand, we construct an example where large noise implies non-identifiability even for generic noise and interactions. Finally, we briefly show that in some simple cases, models with hidden nodes can also be recovered.