On the Convergence of Gradient Descent on Learning Transformers with Residual Connections

Transformer models have emerged as fundamental tools across various scientific and engineering disciplines, owing to their outstanding performance in diverse applications. Despite this empirical success, the theoretical foundations of Transformers remain relatively underdeveloped, particularly in understanding their training dynamics. Existing research predominantly examines isolated components--such as self-attention mechanisms and feedforward networks--without thoroughly investigating the interdependencies between these components, especially when residual connections are present. In this paper, we aim to bridge this gap by analyzing the convergence behavior of a structurally complete yet single-layer Transformer, comprising self-attention, a feedforward network, and residual connections. We demonstrate that, under appropriate initialization, gradient descent exhibits a linear convergence rate, where the convergence speed is determined by the minimum and maximum singular values of the output matrix from the attention layer. Moreover, our analysis reveals that residual connections serve to ameliorate the ill-conditioning of this output matrix, an issue stemming from the low-rank structure imposed by the softmax operation, thereby promoting enhanced optimization stability. We also extend our theoretical findings to a multi-layer Transformer architecture, confirming the linear convergence rate of gradient descent under suitable initialization. Empirical results corroborate our theoretical insights, illustrating the beneficial role of residual connections in promoting convergence stability.

Analyzing Fine-Grained Alignment and Enhancing Vision Understanding in Multimodal Language Models

Achieving better alignment between vision embeddings and Large Language Models (LLMs) is crucial for enhancing the abilities of Multimodal LLMs (MLLMs), particularly for recent models that rely on powerful pretrained vision encoders and LLMs. A common approach to connect the pretrained vision encoder and LLM is through a projector applied after the vision encoder. However, the projector is often trained to enable the LLM to generate captions, and hence the mechanism by which LLMs understand each vision token remains unclear. In this work, we first investigate the role of the projector in compressing vision embeddings and aligning them with word embeddings. We show that the projector significantly compresses visual information, removing redundant details while preserving essential elements necessary for the LLM to understand visual content. We then examine patch-level alignment -- the alignment between each vision patch and its corresponding semantic words -- and propose a *multi-semantic alignment hypothesis*. Our analysis indicates that the projector trained by caption loss improves patch-level alignment but only to a limited extent, resulting in weak and coarse alignment. To address this issue, we propose *patch-aligned training* to efficiently enhance patch-level alignment. Our experiments show that patch-aligned training (1) achieves stronger compression capability and improved patch-level alignment, enabling the MLLM to generate higher-quality captions, (2) improves the MLLM's performance by 16% on referring expression grounding tasks, 4% on question-answering tasks, and 3% on modern instruction-following benchmarks when using the same supervised fine-tuning (SFT) setting. The proposed method can be easily extended to other multimodal models.

From Compression to Expansion: A Layerwise Analysis of In-Context Learning

In-context learning (ICL) enables large language models (LLMs) to adapt to new tasks without weight updates by learning from demonstration sequences. While ICL shows strong empirical performance, its internal representational mechanisms are not yet well understood. In this work, we conduct a statistical geometric analysis of ICL representations to investigate how task-specific information is captured across layers. Our analysis reveals an intriguing phenomenon, which we term *Layerwise Compression-Expansion*: early layers progressively produce compact and discriminative representations that encode task information from the input demonstrations, while later layers expand these representations to incorporate the query and generate the prediction. This phenomenon is observed consistently across diverse tasks and a range of contemporary LLM architectures. We demonstrate that it has important implications for ICL performance -- improving with model size and the number of demonstrations -- and for robustness in the presence of noisy examples. To further understand the effect of the compact task representation, we propose a bias-variance decomposition and provide a theoretical analysis showing how attention mechanisms contribute to reducing both variance and bias, thereby enhancing performance as the number of demonstrations increases. Our findings reveal an intriguing layerwise dynamic in ICL, highlight how structured representations emerge within LLMs, and showcase that analyzing internal representations can facilitate a deeper understanding of model behavior.

On Layer-wise Representation Similarity: Application for Multi-Exit Models with a Single Classifier

Analyzing the similarity of internal representations within and across different models has been an important technique for understanding the behavior of deep neural networks. Most existing methods for analyzing the similarity between representations of high dimensions, such as those based on Canonical Correlation Analysis (CCA) and widely used Centered Kernel Alignment (CKA), rely on statistical properties of the representations for a set of data points. In this paper, we focus on transformer models and study the similarity of representations between the hidden layers of individual transformers. In this context, we show that a simple sample-wise cosine similarity metric is capable of capturing the similarity and aligns with the complicated CKA. Our experimental results on common transformers reveal that representations across layers are positively correlated, albeit the similarity decreases when layers are far apart. We then propose an aligned training approach to enhance the similarity between internal representations, with trained models that enjoy the following properties: (1) the last-layer classifier can be directly applied right after any hidden layers, yielding intermediate layer accuracies much higher than those under standard training, (2) the layer-wise accuracies monotonically increase and reveal the minimal depth needed for the given task, (3) when served as multi-exit models, they achieve on-par performance with standard multi-exit architectures which consist of additional classifiers designed for early exiting in shallow layers. To our knowledge, our work is the first to show that one common classifier is sufficient for multi-exit models. We conduct experiments on both vision and NLP tasks to demonstrate the performance of the proposed aligned training.

AdaContour: Adaptive Contour Descriptor with Hierarchical Representation

Existing angle-based contour descriptors suffer from lossy representation for non-starconvex shapes. By and large, this is the result of the shape being registered with a single global inner center and a set of radii corresponding to a polar coordinate parameterization. In this paper, we propose AdaContour, an adaptive contour descriptor that uses multiple local representations to desirably characterize complex shapes. After hierarchically encoding object shapes in a training set and constructing a contour matrix of all subdivided regions, we compute a robust low-rank robust subspace and approximate each local contour by linearly combining the shared basis vectors to represent an object. Experiments show that AdaContour is able to represent shapes more accurately and robustly than other descriptors while retaining effectiveness. We validate AdaContour by integrating it into off-the-shelf detectors to enable instance segmentation which demonstrates faithful performance. The code is available at https://github.com/tding1/AdaContour.

The Efficiency Spectrum of Large Language Models: An Algorithmic Survey

The rapid growth of Large Language Models (LLMs) has been a driving force in transforming various domains, reshaping the artificial general intelligence landscape. However, the increasing computational and memory demands of these models present substantial challenges, hindering both academic research and practical applications. To address these issues, a wide array of methods, including both algorithmic and hardware solutions, have been developed to enhance the efficiency of LLMs. This survey delivers a comprehensive review of algorithmic advancements aimed at improving LLM efficiency. Unlike other surveys that typically focus on specific areas such as training or model compression, this paper examines the multi-faceted dimensions of efficiency essential for the end-to-end algorithmic development of LLMs. Specifically, it covers various topics related to efficiency, including scaling laws, data utilization, architectural innovations, training and tuning strategies, and inference techniques. This paper aims to serve as a valuable resource for researchers and practitioners, laying the groundwork for future innovations in this critical research area. Our repository of relevant references is maintained at url{https://github.com/tding1/Efficient-LLM-Survey}.

DREAM: Diffusion Rectification and Estimation-Adaptive Models

We present DREAM, a novel training framework representing Diffusion Rectification and Estimation-Adaptive Models, requiring minimal code changes (just three lines) yet significantly enhancing the alignment of training with sampling in diffusion models. DREAM features two components: diffusion rectification, which adjusts training to reflect the sampling process, and estimation adaptation, which balances perception against distortion. When applied to image super-resolution (SR), DREAM adeptly navigates the tradeoff between minimizing distortion and preserving high image quality. Experiments demonstrate DREAM's superiority over standard diffusion-based SR methods, showing a $2$ to $3\times $ faster training convergence and a $10$ to $20\times$ reduction in necessary sampling steps to achieve comparable or superior results. We hope DREAM will inspire a rethinking of diffusion model training paradigms.

Generalized Neural Collapse for a Large Number of Classes

Neural collapse provides an elegant mathematical characterization of learned last layer representations (a.k.a. features) and classifier weights in deep classification models. Such results not only provide insights but also motivate new techniques for improving practical deep models. However, most of the existing empirical and theoretical studies in neural collapse focus on the case that the number of classes is small relative to the dimension of the feature space. This paper extends neural collapse to cases where the number of classes are much larger than the dimension of feature space, which broadly occur for language models, retrieval systems, and face recognition applications. We show that the features and classifier exhibit a generalized neural collapse phenomenon, where the minimum one-vs-rest margins is maximized.We provide empirical study to verify the occurrence of generalized neural collapse in practical deep neural networks. Moreover, we provide theoretical study to show that the generalized neural collapse provably occurs under unconstrained feature model with spherical constraint, under certain technical conditions on feature dimension and number of classes.

Principled and Efficient Transfer Learning of Deep Models via Neural Collapse

With the ever-growing model size and the limited availability of labeled training data, transfer learning has become an increasingly popular approach in many science and engineering domains. For classification problems, this work delves into the mystery of transfer learning through an intriguing phenomenon termed neural collapse (NC), where the last-layer features and classifiers of learned deep networks satisfy: (i) the within-class variability of the features collapses to zero, and (ii) the between-class feature means are maximally and equally separated. Through the lens of NC, our findings for transfer learning are the following: (i) when pre-training models, preventing intra-class variability collapse (to a certain extent) better preserves the intrinsic structures of the input data, so that it leads to better model transferability; (ii) when fine-tuning models on downstream tasks, obtaining features with more NC on downstream data results in better test accuracy on the given task. The above results not only demystify many widely used heuristics in model pre-training (e.g., data augmentation, projection head, self-supervised learning), but also leads to more efficient and principled fine-tuning method on downstream tasks that we demonstrate through extensive experimental results.

Are All Losses Created Equal: A Neural Collapse Perspective

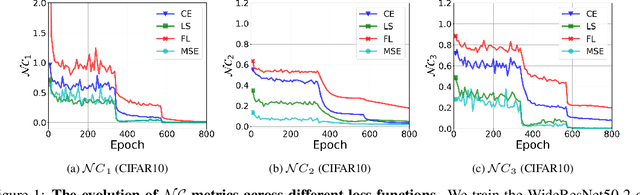
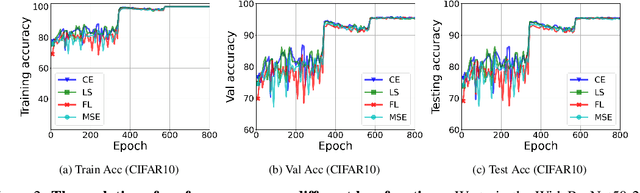
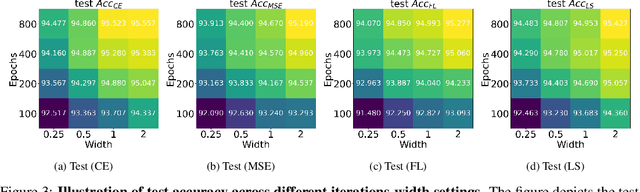
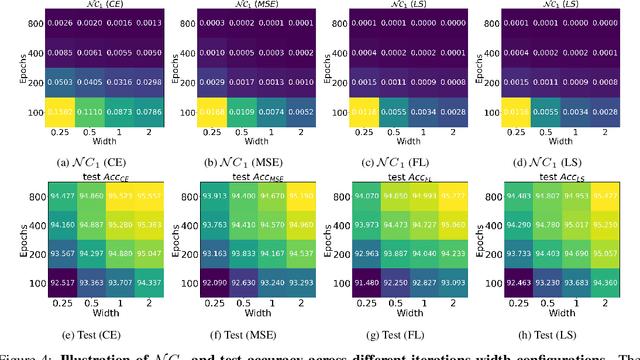
While cross entropy (CE) is the most commonly used loss to train deep neural networks for classification tasks, many alternative losses have been developed to obtain better empirical performance. Among them, which one is the best to use is still a mystery, because there seem to be multiple factors affecting the answer, such as properties of the dataset, the choice of network architecture, and so on. This paper studies the choice of loss function by examining the last-layer features of deep networks, drawing inspiration from a recent line work showing that the global optimal solution of CE and mean-square-error (MSE) losses exhibits a Neural Collapse phenomenon. That is, for sufficiently large networks trained until convergence, (i) all features of the same class collapse to the corresponding class mean and (ii) the means associated with different classes are in a configuration where their pairwise distances are all equal and maximized. We extend such results and show through global solution and landscape analyses that a broad family of loss functions including commonly used label smoothing (LS) and focal loss (FL) exhibits Neural Collapse. Hence, all relevant losses(i.e., CE, LS, FL, MSE) produce equivalent features on training data. Based on the unconstrained feature model assumption, we provide either the global landscape analysis for LS loss or the local landscape analysis for FL loss and show that the (only!) global minimizers are neural collapse solutions, while all other critical points are strict saddles whose Hessian exhibit negative curvature directions either in the global scope for LS loss or in the local scope for FL loss near the optimal solution. The experiments further show that Neural Collapse features obtained from all relevant losses lead to largely identical performance on test data as well, provided that the network is sufficiently large and trained until convergence.