Reinforcement Learning in Low-Rank MDPs with Density Features

MDPs with low-rank transitions -- that is, the transition matrix can be factored into the product of two matrices, left and right -- is a highly representative structure that enables tractable learning. The left matrix enables expressive function approximation for value-based learning and has been studied extensively. In this work, we instead investigate sample-efficient learning with density features, i.e., the right matrix, which induce powerful models for state-occupancy distributions. This setting not only sheds light on leveraging unsupervised learning in RL, but also enables plug-in solutions for convex RL. In the offline setting, we propose an algorithm for off-policy estimation of occupancies that can handle non-exploratory data. Using this as a subroutine, we further devise an online algorithm that constructs exploratory data distributions in a level-by-level manner. As a central technical challenge, the additive error of occupancy estimation is incompatible with the multiplicative definition of data coverage. In the absence of strong assumptions like reachability, this incompatibility easily leads to exponential error blow-up, which we overcome via novel technical tools. Our results also readily extend to the representation learning setting, when the density features are unknown and must be learned from an exponentially large candidate set.

On the Statistical Efficiency of Reward-Free Exploration in Non-Linear RL

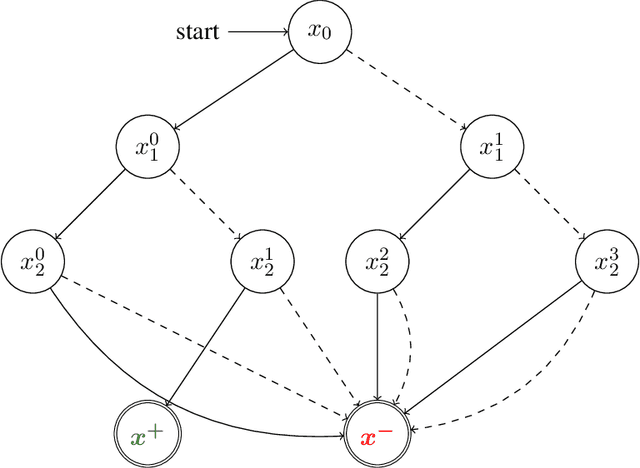
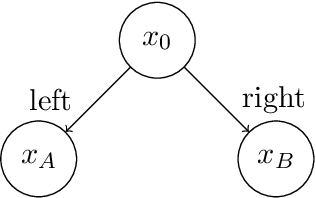
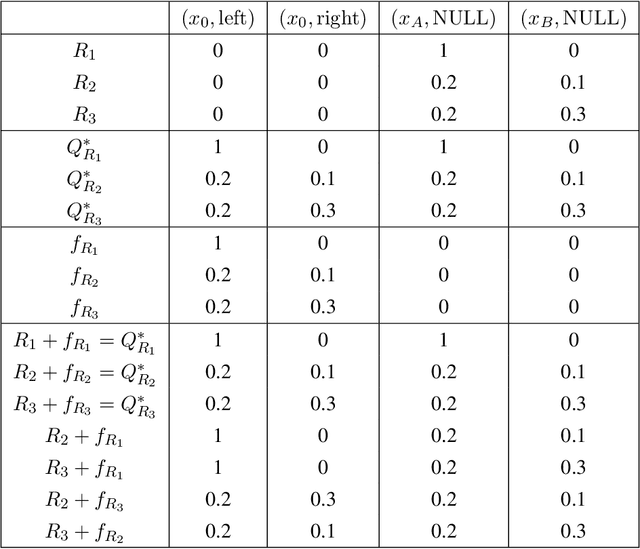
We study reward-free reinforcement learning (RL) under general non-linear function approximation, and establish sample efficiency and hardness results under various standard structural assumptions. On the positive side, we propose the RFOLIVE (Reward-Free OLIVE) algorithm for sample-efficient reward-free exploration under minimal structural assumptions, which covers the previously studied settings of linear MDPs (Jin et al., 2020b), linear completeness (Zanette et al., 2020b) and low-rank MDPs with unknown representation (Modi et al., 2021). Our analyses indicate that the explorability or reachability assumptions, previously made for the latter two settings, are not necessary statistically for reward-free exploration. On the negative side, we provide a statistical hardness result for both reward-free and reward-aware exploration under linear completeness assumptions when the underlying features are unknown, showing an exponential separation between low-rank and linear completeness settings.

Offline Reinforcement Learning Under Value and Density-Ratio Realizability: the Power of Gaps

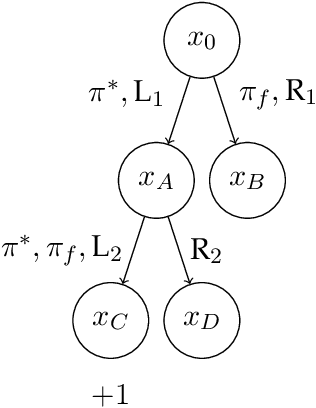
We consider a challenging theoretical problem in offline reinforcement learning (RL): obtaining sample-efficiency guarantees with a dataset lacking sufficient coverage, under only realizability-type assumptions for the function approximators. While the existing theory has addressed learning under realizability and under non-exploratory data separately, no work has been able to address both simultaneously (except for a concurrent work which we compare in detail). Under an additional gap assumption, we provide guarantees to a simple pessimistic algorithm based on a version space formed by marginalized importance sampling, and the guarantee only requires the data to cover the optimal policy and the function classes to realize the optimal value and density-ratio functions. While similar gap assumptions have been used in other areas of RL theory, our work is the first to identify the utility and the novel mechanism of gap assumptions in offline RL with weak function approximation.

Towards Deployment-Efficient Reinforcement Learning: Lower Bound and Optimality

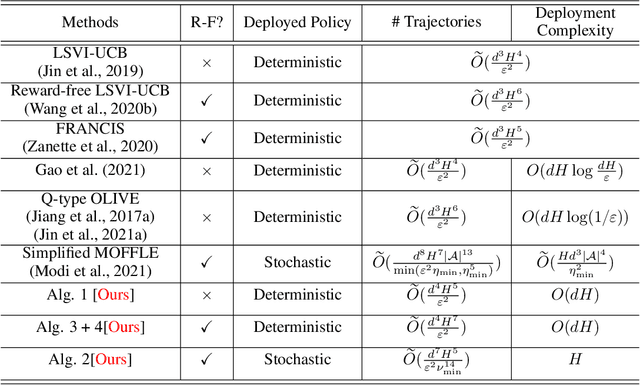
Deployment efficiency is an important criterion for many real-world applications of reinforcement learning (RL). Despite the community's increasing interest, there lacks a formal theoretical formulation for the problem. In this paper, we propose such a formulation for deployment-efficient RL (DE-RL) from an "optimization with constraints" perspective: we are interested in exploring an MDP and obtaining a near-optimal policy within minimal \emph{deployment complexity}, whereas in each deployment the policy can sample a large batch of data. Using finite-horizon linear MDPs as a concrete structural model, we reveal the fundamental limit in achieving deployment efficiency by establishing information-theoretic lower bounds, and provide algorithms that achieve the optimal deployment efficiency. Moreover, our formulation for DE-RL is flexible and can serve as a building block for other practically relevant settings; we give "Safe DE-RL" and "Sample-Efficient DE-RL" as two examples, which may be worth future investigation.

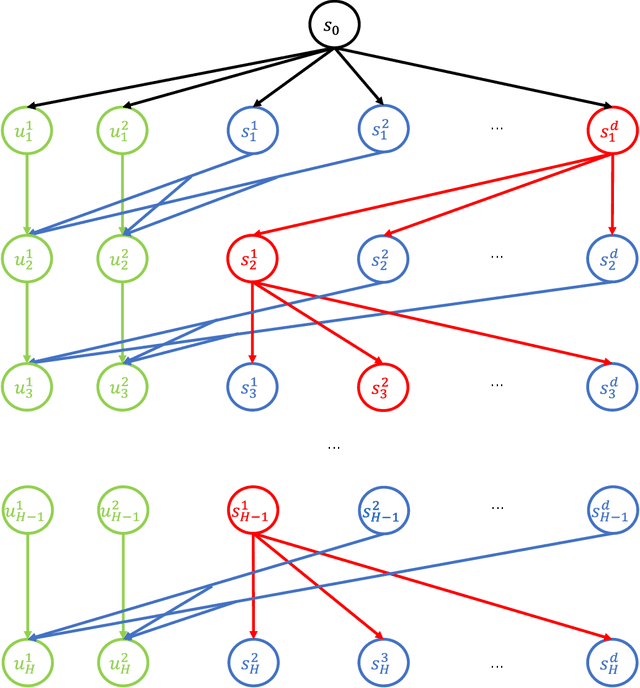
Model-free Representation Learning and Exploration in Low-rank MDPs

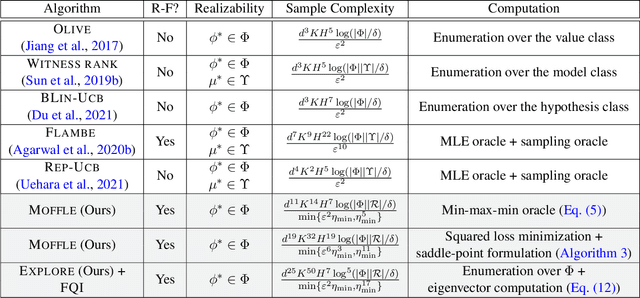
The low rank MDP has emerged as an important model for studying representation learning and exploration in reinforcement learning. With a known representation, several model-free exploration strategies exist. In contrast, all algorithms for the unknown representation setting are model-based, thereby requiring the ability to model the full dynamics. In this work, we present the first model-free representation learning algorithms for low rank MDPs. The key algorithmic contribution is a new minimax representation learning objective, for which we provide variants with differing tradeoffs in their statistical and computational properties. We interleave this representation learning step with an exploration strategy to cover the state space in a reward-free manner. The resulting algorithms are provably sample efficient and can accommodate general function approximation to scale to complex environments.

Improved Worst-Case Regret Bounds for Randomized Least-Squares Value Iteration

This paper studies regret minimization with randomized value functions in reinforcement learning. In tabular finite-horizon Markov Decision Processes, we introduce a clipping variant of one classical Thompson Sampling (TS)-like algorithm, randomized least-squares value iteration (RLSVI). We analyze the algorithm using a novel intertwined regret decomposition. Our $\tilde{\mathrm{O}}(H^2S\sqrt{AT})$ high-probability worst-case regret bound improves the previous sharpest worst-case regret bounds for RLSVI and matches the existing state-of-the-art worst-case TS-based regret bounds.

Nonstationary Reinforcement Learning with Linear Function Approximation

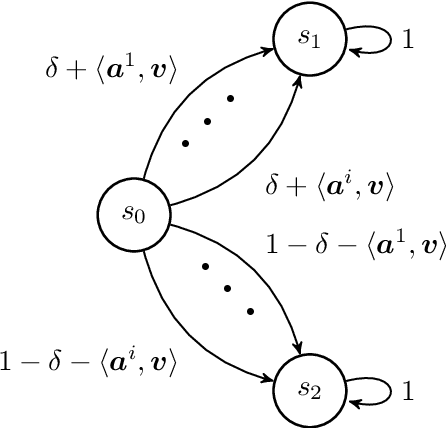
We consider reinforcement learning (RL) in episodic Markov decision processes (MDPs) with linear function approximation under drifting environment. Specifically, both the reward and state transition functions can evolve over time, as long as their respective total variations, quantified by suitable metrics, do not exceed certain \textit{variation budgets}. We first develop the $\texttt{LSVI-UCB-Restart}$ algorithm, an optimistic modification of least-squares value iteration combined with periodic restart, and establish its dynamic regret bound when variation budgets are known. We then propose a parameter-free algorithm, $\texttt{Ada-LSVI-UCB-Restart}$, that works without knowing the variation budgets, but with a slightly worse dynamic regret bound. We also derive the first minimax dynamic regret lower bound for nonstationary MDPs to show that our proposed algorithms are near-optimal. As a byproduct, we establish a minimax regret lower bound for linear MDPs, which is unsolved by \cite{jin2020provably}. In addition, we provide numerical experiments to demonstrate the effectiveness of our proposed algorithms. As far as we know, this is the first dynamic regret analysis in nonstationary reinforcement learning with function approximation.

Accelerating Nonconvex Learning via Replica Exchange Langevin Diffusion

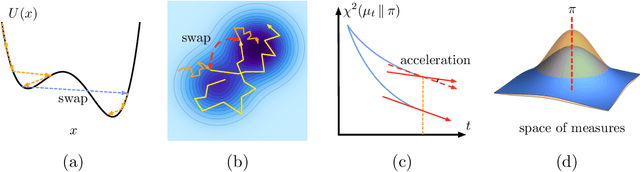
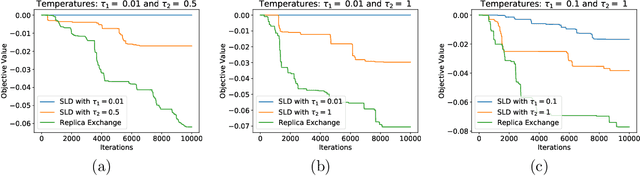
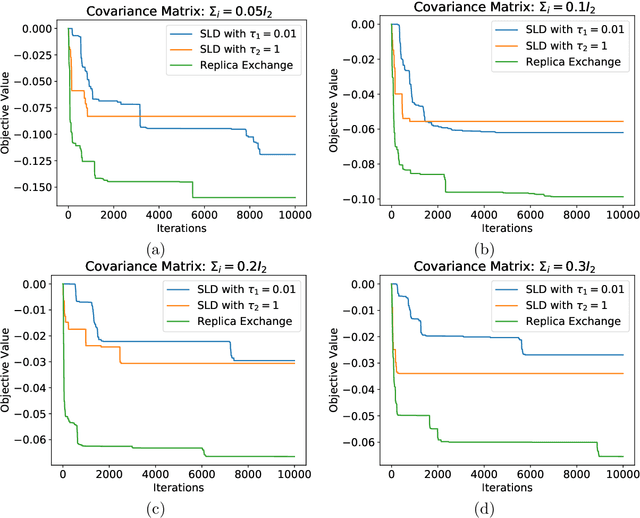
Langevin diffusion is a powerful method for nonconvex optimization, which enables the escape from local minima by injecting noise into the gradient. In particular, the temperature parameter controlling the noise level gives rise to a tradeoff between ``global exploration'' and ``local exploitation'', which correspond to high and low temperatures. To attain the advantages of both regimes, we propose to use replica exchange, which swaps between two Langevin diffusions with different temperatures. We theoretically analyze the acceleration effect of replica exchange from two perspectives: (i) the convergence in \chi^2-divergence, and (ii) the large deviation principle. Such an acceleration effect allows us to faster approach the global minima. Furthermore, by discretizing the replica exchange Langevin diffusion, we obtain a discrete-time algorithm. For such an algorithm, we quantify its discretization error in theory and demonstrate its acceleration effect in practice.

Information-Theoretic Considerations in Batch Reinforcement Learning

Value-function approximation methods that operate in batch mode have foundational importance to reinforcement learning (RL). Finite sample guarantees for these methods often crucially rely on two types of assumptions: (1) mild distribution shift, and (2) representation conditions that are stronger than realizability. However, the necessity ("why do we need them?") and the naturalness ("when do they hold?") of such assumptions have largely eluded the literature. In this paper, we revisit these assumptions and provide theoretical results towards answering the above questions, and make steps towards a deeper understanding of value-function approximation.

Efficient Localized Inference for Large Graphical Models

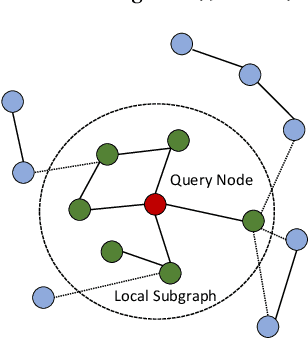
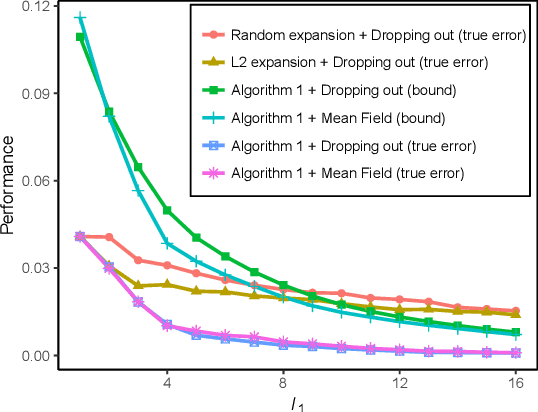
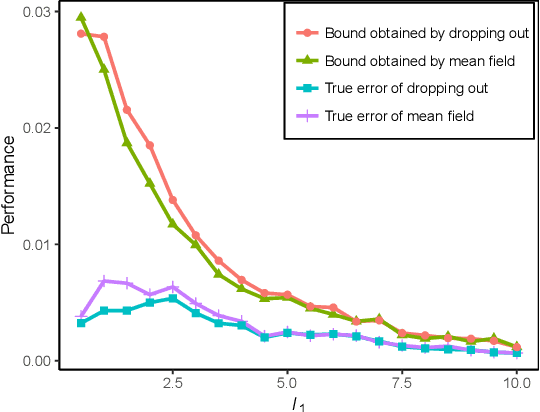
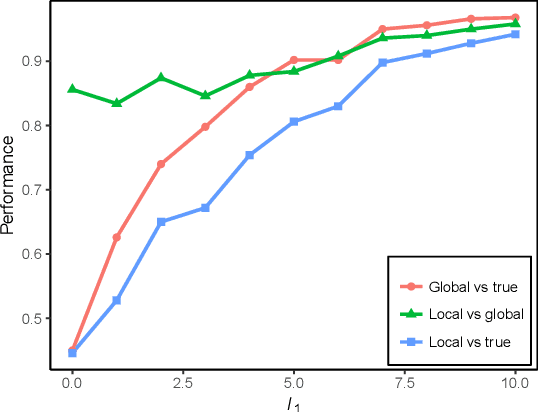
We propose a new localized inference algorithm for answering marginalization queries in large graphical models with the correlation decay property. Given a query variable and a large graphical model, we define a much smaller model in a local region around the query variable in the target model so that the marginal distribution of the query variable can be accurately approximated. We introduce two approximation error bounds based on the Dobrushin's comparison theorem and apply our bounds to derive a greedy expansion algorithm that efficiently guides the selection of neighbor nodes for localized inference. We verify our theoretical bounds on various datasets and demonstrate that our localized inference algorithm can provide fast and accurate approximation for large graphical models.