ML-DCN: Masked Low-Rank Deep Crossing Network Towards Scalable Ads Click-through Rate Prediction at Pinterest

Deep learning recommendation systems rely on feature interaction modules to model complex user-item relationships across sparse categorical and dense features. In large-scale ad ranking, increasing model capacity is a promising path to improving both predictive performance and business outcomes, yet production serving budgets impose strict constraints on latency and FLOPs. This creates a central tension: we want interaction modules that both scale effectively with additional compute and remain compute-efficient at serving time. In this work, we study how to scale feature interaction modules under a fixed serving budget. We find that naively scaling DCNv2 and MaskNet, despite their widespread adoption in industry, yields rapidly diminishing offline gains in the Pinterest ads ranking system. To overcome aforementioned limitations, we propose ML-DCN, an interaction module that integrates an instance-conditioned mask into a low-rank crossing layer, enabling per-example selection and amplification of salient interaction directions while maintaining efficient computation. This novel architecture combines the strengths of DCNv2 and MaskNet, scales efficiently with increased compute, and achieves state-of-the-art performance. Experiments on a large internal Pinterest ads dataset show that ML-DCN achieves higher AUC than DCNv2, MaskNet, and recent scaling-oriented alternatives at matched FLOPs, and it scales more favorably overall as compute increases, exhibiting a stronger AUC-FLOPs trade-off. Finally, online A/B tests demonstrate statistically significant improvements in key ads metrics (including CTR and click-quality measures) and ML-DCN has been deployed in the production system with neutral serving cost.

Accelerated Federated Learning with Decoupled Adaptive Optimization

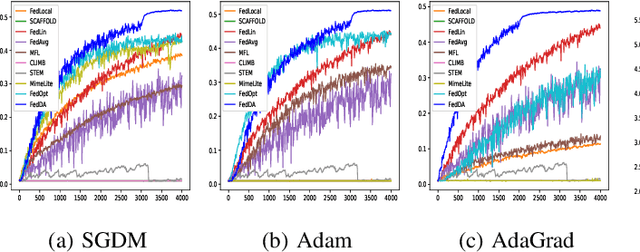
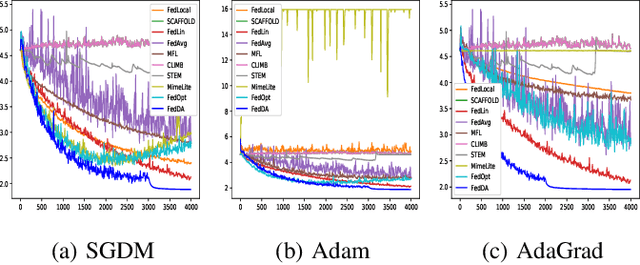
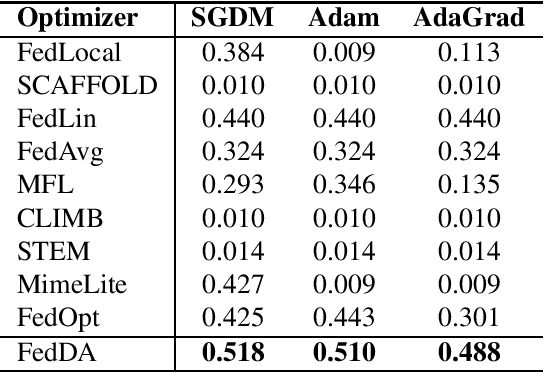
The federated learning (FL) framework enables edge clients to collaboratively learn a shared inference model while keeping privacy of training data on clients. Recently, many heuristics efforts have been made to generalize centralized adaptive optimization methods, such as SGDM, Adam, AdaGrad, etc., to federated settings for improving convergence and accuracy. However, there is still a paucity of theoretical principles on where to and how to design and utilize adaptive optimization methods in federated settings. This work aims to develop novel adaptive optimization methods for FL from the perspective of dynamics of ordinary differential equations (ODEs). First, an analytic framework is established to build a connection between federated optimization methods and decompositions of ODEs of corresponding centralized optimizers. Second, based on this analytic framework, a momentum decoupling adaptive optimization method, FedDA, is developed to fully utilize the global momentum on each local iteration and accelerate the training convergence. Last but not least, full batch gradients are utilized to mimic centralized optimization in the end of the training process to ensure the convergence and overcome the possible inconsistency caused by adaptive optimization methods.

Input-agnostic Certified Group Fairness via Gaussian Parameter Smoothing

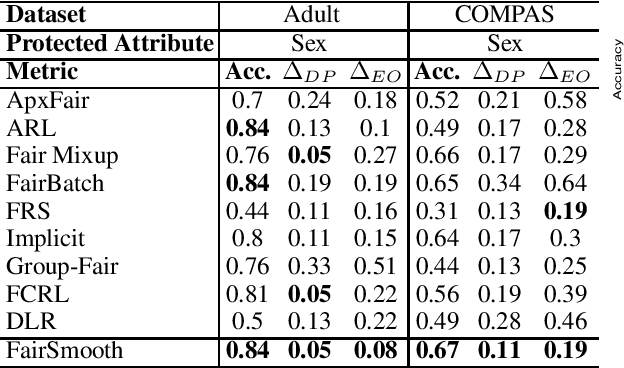
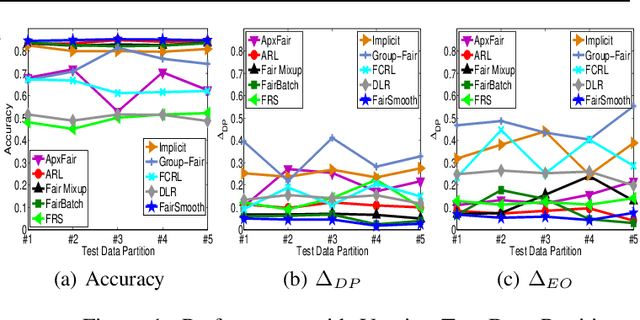
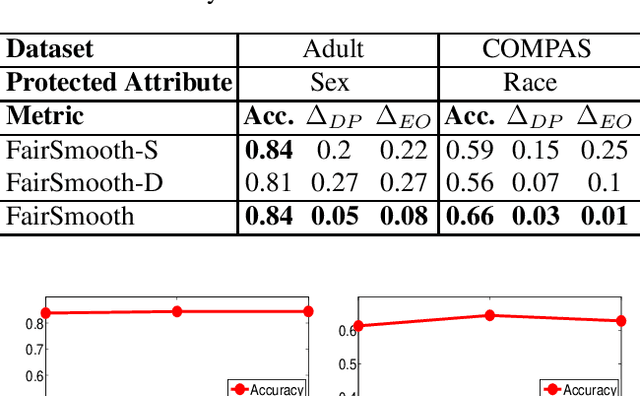
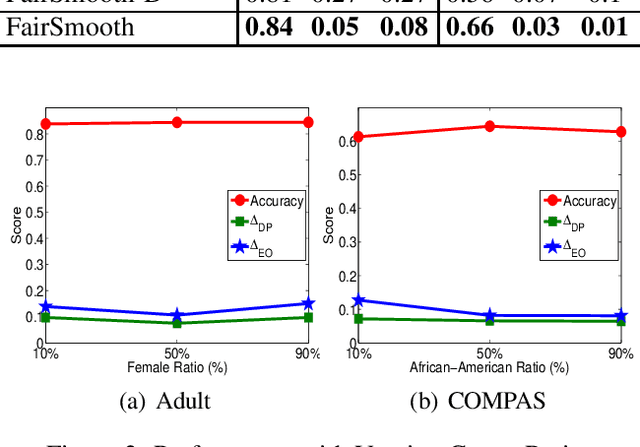
Only recently, researchers attempt to provide classification algorithms with provable group fairness guarantees. Most of these algorithms suffer from harassment caused by the requirement that the training and deployment data follow the same distribution. This paper proposes an input-agnostic certified group fairness algorithm, FairSmooth, for improving the fairness of classification models while maintaining the remarkable prediction accuracy. A Gaussian parameter smoothing method is developed to transform base classifiers into their smooth versions. An optimal individual smooth classifier is learnt for each group with only the data regarding the group and an overall smooth classifier for all groups is generated by averaging the parameters of all the individual smooth ones. By leveraging the theory of nonlinear functional analysis, the smooth classifiers are reformulated as output functions of a Nemytskii operator. Theoretical analysis is conducted to derive that the Nemytskii operator is smooth and induces a Frechet differentiable smooth manifold. We theoretically demonstrate that the smooth manifold has a global Lipschitz constant that is independent of the domain of the input data, which derives the input-agnostic certified group fairness.