Cascaded Mutual Modulation for Visual Reasoning

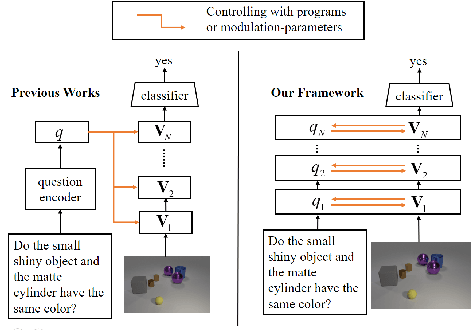
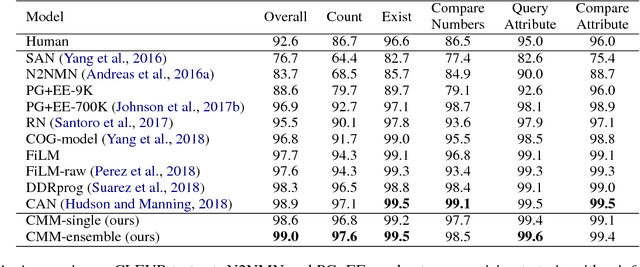
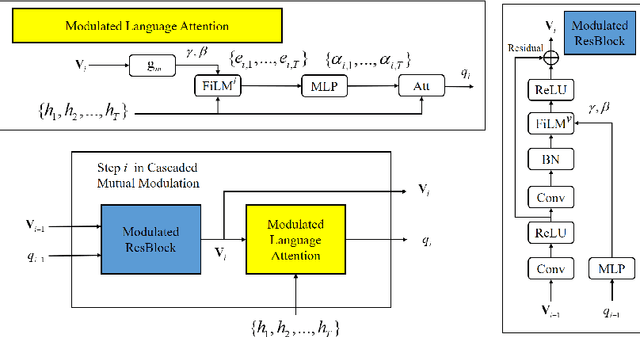
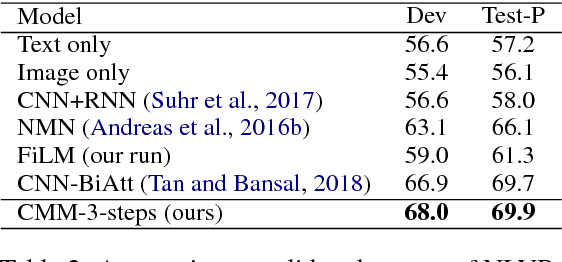
Visual reasoning is a special visual question answering problem that is multi-step and compositional by nature, and also requires intensive text-vision interactions. We propose CMM: Cascaded Mutual Modulation as a novel end-to-end visual reasoning model. CMM includes a multi-step comprehension process for both question and image. In each step, we use a Feature-wise Linear Modulation (FiLM) technique to enable textual/visual pipeline to mutually control each other. Experiments show that CMM significantly outperforms most related models, and reach state-of-the-arts on two visual reasoning benchmarks: CLEVR and NLVR, collected from both synthetic and natural languages. Ablation studies confirm that both our multistep framework and our visual-guided language modulation are critical to the task. Our code is available at https://github.com/FlamingHorizon/CMM-VR.

Seeded Graph Matching via Large Neighborhood Statistics

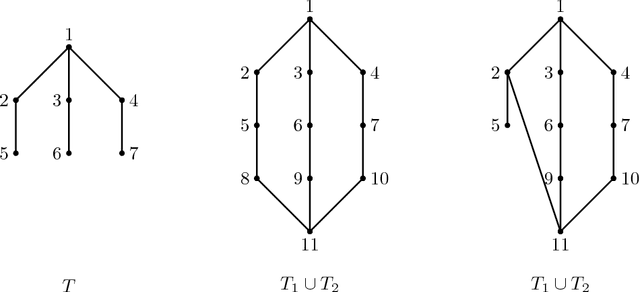
We study a well known noisy model of the graph isomorphism problem. In this model, the goal is to perfectly recover the vertex correspondence between two edge-correlated Erd\H{o}s-R\'{e}nyi random graphs, with an initial seed set of correctly matched vertex pairs revealed as side information. For seeded problems, our result provides a significant improvement over previously known results. We show that it is possible to achieve the information-theoretic limit of graph sparsity in time polynomial in the number of vertices $n$. Moreover, we show the number of seeds needed for exact recovery in polynomial-time can be as low as $n^{3\epsilon}$ in the sparse graph regime (with the average degree smaller than $n^{\epsilon}$) and $\Omega(\log n)$ in the dense graph regime. Our results also shed light on the unseeded problem. In particular, we give sub-exponential time algorithms for sparse models and an $n^{O(\log n)}$ algorithm for dense models for some parameters, including some that are not covered by recent results of Barak et al.

Securing Distributed Machine Learning in High Dimensions

Standard distributed machine learning frameworks require collecting the training data from data providers and storing it in a datacenter. To ease privacy concerns, alternative distributed machine learning frameworks (such as {\em Federated Learning}) have been proposed, wherein the training data is kept confidential by its providers from the learner, and the learner learns the model by communicating with data providers. However, such frameworks suffer from serious security risks, as data providers are vulnerable to adversarial attacks and the learner lacks of enough administrative power. We assume in each communication round, up to $q$ out of the $m$ data providers/workers suffer Byzantine faults. Each worker keeps a local sample of size $n$ and the total sample size is $N=nm$. Of particular interest is the high-dimensional regime, where the local sample size $n$ is much smaller than the model dimension $d$. We propose a secured variant of the gradient descent method and show that it tolerates up to a constant fraction of Byzantine workers. Moreover, we show the statistical estimation error of the iterates converges in $O(\log N)$ rounds to $O(\sqrt{q/N} + \sqrt{d/N})$, which is larger than the minimax-optimal error rate $O(\sqrt{d/N})$ in the failure-free setting by at most an additive term $O(\sqrt{q/N})$. As long as $q=O(d)$, our proposed algorithm achieves the optimal error rate $O(\sqrt{d/N})$. The core of our method is a robust gradient aggregator based on the iterative filtering algorithm proposed by Steinhardt et al. We establish a {\em uniform} concentration of the sample covariance matrix of gradients, and show that the aggregated gradient, as a function of model parameter, converges uniformly to the true gradient function. As a by-product, we develop a new concentration inequality for sample covariance matrices, which might be of independent interest.

Hidden Hamiltonian Cycle Recovery via Linear Programming

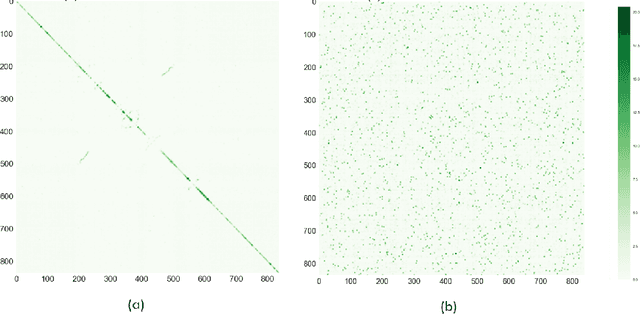
We introduce the problem of hidden Hamiltonian cycle recovery, where there is an unknown Hamiltonian cycle in an $n$-vertex complete graph that needs to be inferred from noisy edge measurements. The measurements are independent and distributed according to $\calP_n$ for edges in the cycle and $\calQ_n$ otherwise. This formulation is motivated by a problem in genome assembly, where the goal is to order a set of contigs (genome subsequences) according to their positions on the genome using long-range linking measurements between the contigs. Computing the maximum likelihood estimate in this model reduces to a Traveling Salesman Problem (TSP). Despite the NP-hardness of TSP, we show that a simple linear programming (LP) relaxation, namely the fractional $2$-factor (F2F) LP, recovers the hidden Hamiltonian cycle with high probability as $n \to \infty$ provided that $\alpha_n - \log n \to \infty$, where $\alpha_n \triangleq -2 \log \int \sqrt{d P_n d Q_n}$ is the R\'enyi divergence of order $\frac{1}{2}$. This condition is information-theoretically optimal in the sense that, under mild distributional assumptions, $\alpha_n \geq (1+o(1)) \log n$ is necessary for any algorithm to succeed regardless of the computational cost. Departing from the usual proof techniques based on dual witness construction, the analysis relies on the combinatorial characterization (in particular, the half-integrality) of the extreme points of the F2F polytope. Represented as bicolored multi-graphs, these extreme points are further decomposed into simpler "blossom-type" structures for the large deviation analysis and counting arguments. Evaluation of the algorithm on real data shows improvements over existing approaches.

Recovering a Hidden Community Beyond the Kesten-Stigum Threshold in $O(|E| \log^*|V|)$ Time

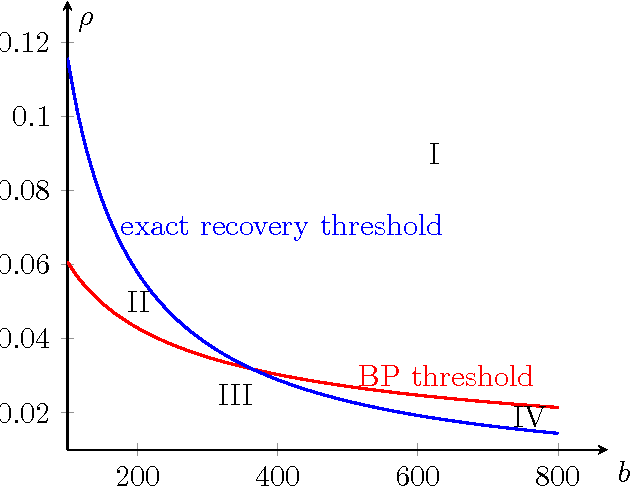
Community detection is considered for a stochastic block model graph of n vertices, with K vertices in the planted community, edge probability p for pairs of vertices both in the community, and edge probability q for other pairs of vertices. The main focus of the paper is on weak recovery of the community based on the graph G, with o(K) misclassified vertices on average, in the sublinear regime $n^{1-o(1)} \leq K \leq o(n).$ A critical parameter is the effective signal-to-noise ratio $\lambda=K^2(p-q)^2/((n-K)q)$, with $\lambda=1$ corresponding to the Kesten-Stigum threshold. We show that a belief propagation algorithm achieves weak recovery if $\lambda>1/e$, beyond the Kesten-Stigum threshold by a factor of $1/e.$ The belief propagation algorithm only needs to run for $\log^\ast n+O(1) $ iterations, with the total time complexity $O(|E| \log^*n)$, where $\log^*n$ is the iterated logarithm of $n.$ Conversely, if $\lambda \leq 1/e$, no local algorithm can asymptotically outperform trivial random guessing. Furthermore, a linear message-passing algorithm that corresponds to applying power iteration to the non-backtracking matrix of the graph is shown to attain weak recovery if and only if $\lambda>1$. In addition, the belief propagation algorithm can be combined with a linear-time voting procedure to achieve the information limit of exact recovery (correctly classify all vertices with high probability) for all $K \ge \frac{n}{\log n} \left( \rho_{\rm BP} +o(1) \right),$ where $\rho_{\rm BP}$ is a function of $p/q$.

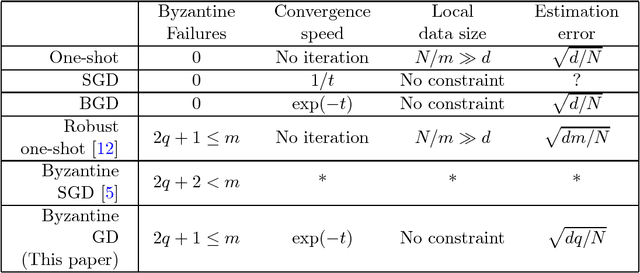
Distributed Statistical Machine Learning in Adversarial Settings: Byzantine Gradient Descent

We consider the problem of distributed statistical machine learning in adversarial settings, where some unknown and time-varying subset of working machines may be compromised and behave arbitrarily to prevent an accurate model from being learned. This setting captures the potential adversarial attacks faced by Federated Learning -- a modern machine learning paradigm that is proposed by Google researchers and has been intensively studied for ensuring user privacy. Formally, we focus on a distributed system consisting of a parameter server and $m$ working machines. Each working machine keeps $N/m$ data samples, where $N$ is the total number of samples. The goal is to collectively learn the underlying true model parameter of dimension $d$. In classical batch gradient descent methods, the gradients reported to the server by the working machines are aggregated via simple averaging, which is vulnerable to a single Byzantine failure. In this paper, we propose a Byzantine gradient descent method based on the geometric median of means of the gradients. We show that our method can tolerate $q \le (m-1)/2$ Byzantine failures, and the parameter estimate converges in $O(\log N)$ rounds with an estimation error of $\sqrt{d(2q+1)/N}$, hence approaching the optimal error rate $\sqrt{d/N}$ in the centralized and failure-free setting. The total computational complexity of our algorithm is of $O((Nd/m) \log N)$ at each working machine and $O(md + kd \log^3 N)$ at the central server, and the total communication cost is of $O(m d \log N)$. We further provide an application of our general results to the linear regression problem. A key challenge arises in the above problem is that Byzantine failures create arbitrary and unspecified dependency among the iterations and the aggregated gradients. We prove that the aggregated gradient converges uniformly to the true gradient function.

Rates of Convergence of Spectral Methods for Graphon Estimation

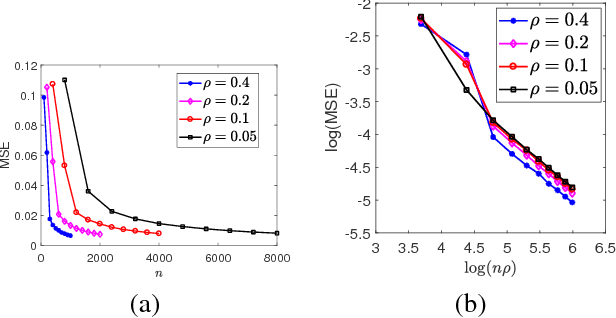
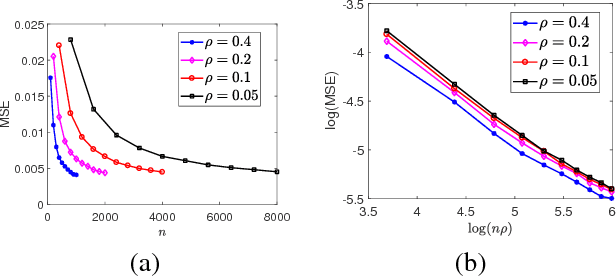
This paper studies the problem of estimating the grahpon model - the underlying generating mechanism of a network. Graphon estimation arises in many applications such as predicting missing links in networks and learning user preferences in recommender systems. The graphon model deals with a random graph of $n$ vertices such that each pair of two vertices $i$ and $j$ are connected independently with probability $\rho \times f(x_i,x_j)$, where $x_i$ is the unknown $d$-dimensional label of vertex $i$, $f$ is an unknown symmetric function, and $\rho$ is a scaling parameter characterizing the graph sparsity. Recent studies have identified the minimax error rate of estimating the graphon from a single realization of the random graph. However, there exists a wide gap between the known error rates of computationally efficient estimation procedures and the minimax optimal error rate. Here we analyze a spectral method, namely universal singular value thresholding (USVT) algorithm, in the relatively sparse regime with the average vertex degree $n\rho=\Omega(\log n)$. When $f$ belongs to H\"{o}lder or Sobolev space with smoothness index $\alpha$, we show the error rate of USVT is at most $(n\rho)^{ -2 \alpha / (2\alpha+d)}$, approaching the minimax optimal error rate $\log (n\rho)/(n\rho)$ for $d=1$ as $\alpha$ increases. Furthermore, when $f$ is analytic, we show the error rate of USVT is at most $\log^d (n\rho)/(n\rho)$. In the special case of stochastic block model with $k$ blocks, the error rate of USVT is at most $k/(n\rho)$, which is larger than the minimax optimal error rate by at most a multiplicative factor $k/\log k$. This coincides with the computational gap observed for community detection. A key step of our analysis is to derive the eigenvalue decaying rate of the edge probability matrix using piecewise polynomial approximations of the graphon function $f$.

Learning from Comparisons and Choices

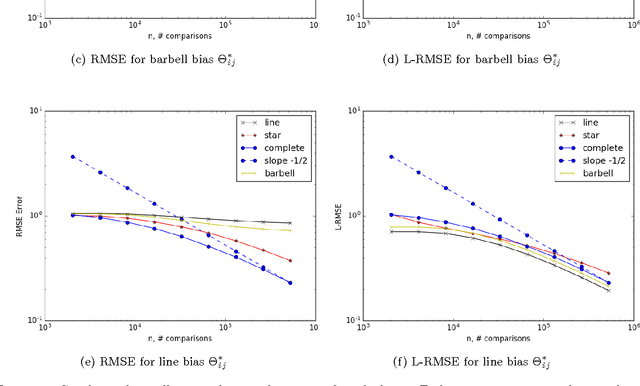
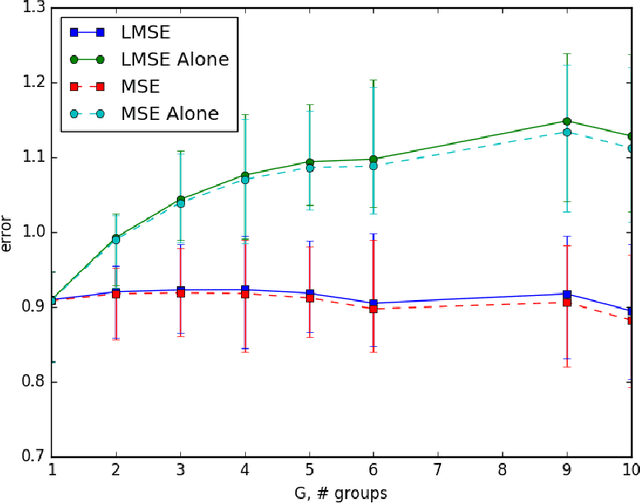
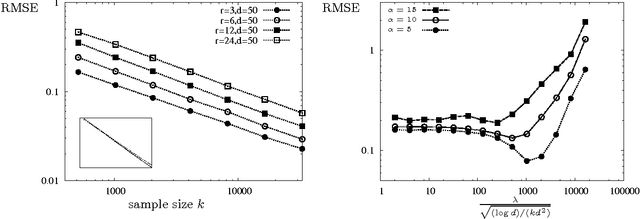
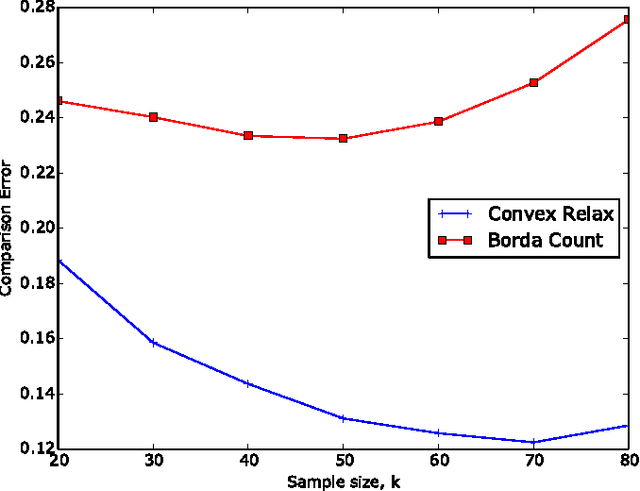
When tracking user-specific online activities, each user's preference is revealed in the form of choices and comparisons. For example, a user's purchase history tracks her choices, i.e. which item was chosen among a subset of offerings. A user's comparisons are observed either explicitly as in movie ratings or implicitly as in viewing times of news articles. Given such individualized ordinal data, we address the problem of collaboratively learning representations of the users and the items. The learned features can be used to predict a user's preference of an unseen item to be used in recommendation systems. This also allows one to compute similarities among users and items to be used for categorization and search. Motivated by the empirical successes of the MultiNomial Logit (MNL) model in marketing and transportation, and also more recent successes in word embedding and crowdsourced image embedding, we pose this problem as learning the MNL model parameters that best explains the data. We propose a convex optimization for learning the MNL model, and show that it is minimax optimal up to a logarithmic factor by comparing its performance to a fundamental lower bound. This characterizes the minimax sample complexity of the problem, and proves that the proposed estimator cannot be improved upon other than by a logarithmic factor. Further, the analysis identifies how the accuracy depends on the topology of sampling via the spectrum of the sampling graph. This provides a guideline for designing surveys when one can choose which items are to be compared. This is accompanies by numerical simulations on synthetic and real datasets confirming our theoretical predictions.

Self-Taught Convolutional Neural Networks for Short Text Clustering

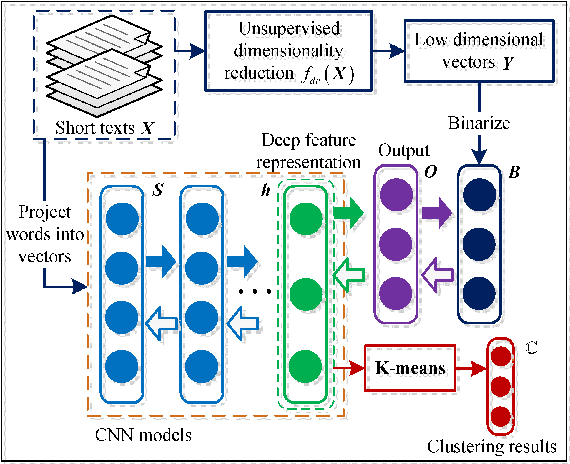
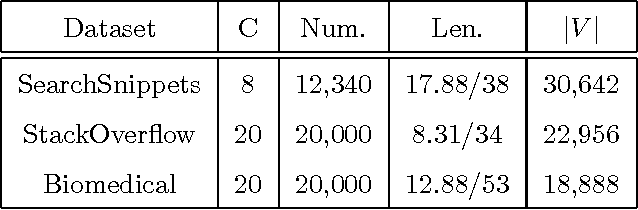
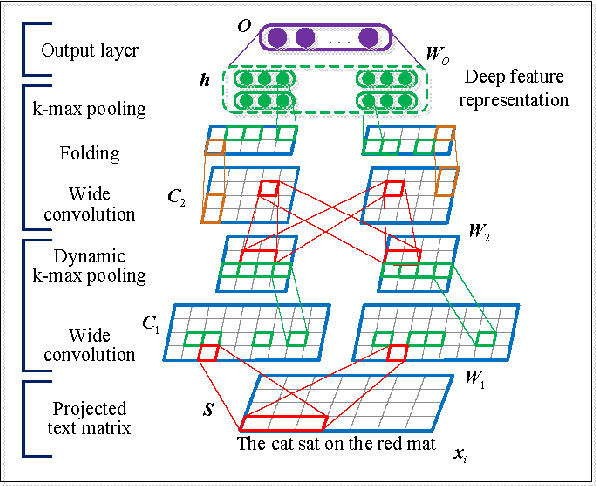
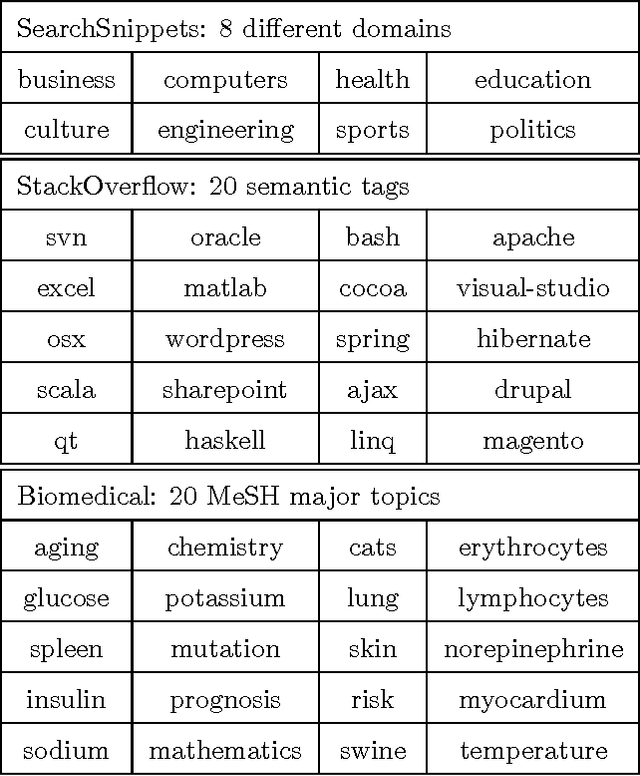
Short text clustering is a challenging problem due to its sparseness of text representation. Here we propose a flexible Self-Taught Convolutional neural network framework for Short Text Clustering (dubbed STC^2), which can flexibly and successfully incorporate more useful semantic features and learn non-biased deep text representation in an unsupervised manner. In our framework, the original raw text features are firstly embedded into compact binary codes by using one existing unsupervised dimensionality reduction methods. Then, word embeddings are explored and fed into convolutional neural networks to learn deep feature representations, meanwhile the output units are used to fit the pre-trained binary codes in the training process. Finally, we get the optimal clusters by employing K-means to cluster the learned representations. Extensive experimental results demonstrate that the proposed framework is effective, flexible and outperform several popular clustering methods when tested on three public short text datasets.

Text Classification Improved by Integrating Bidirectional LSTM with Two-dimensional Max Pooling

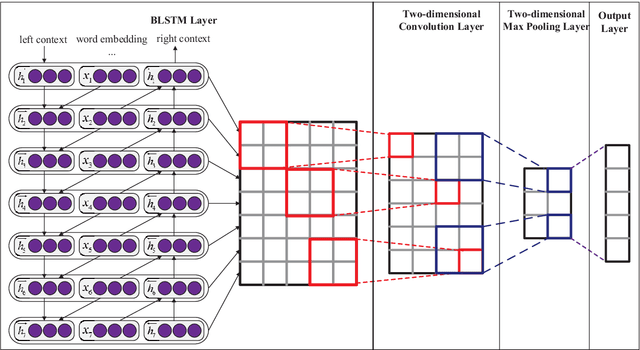
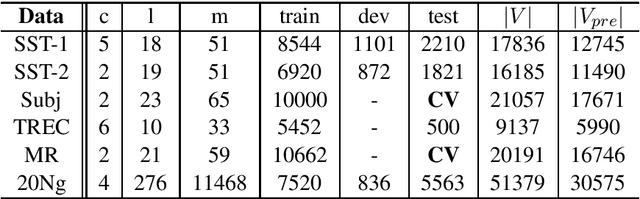
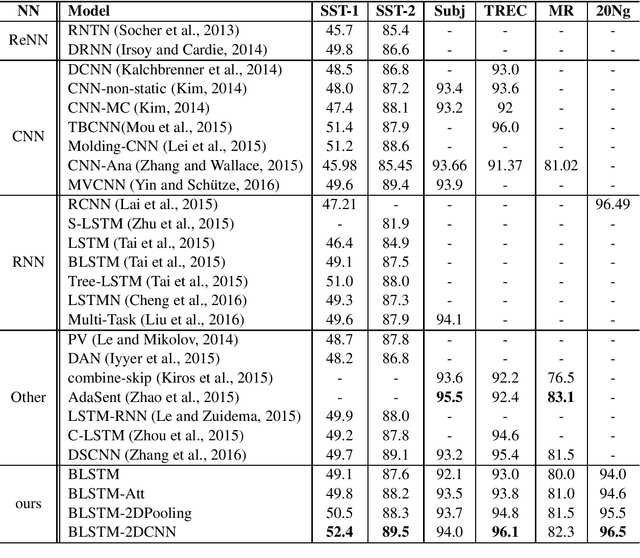
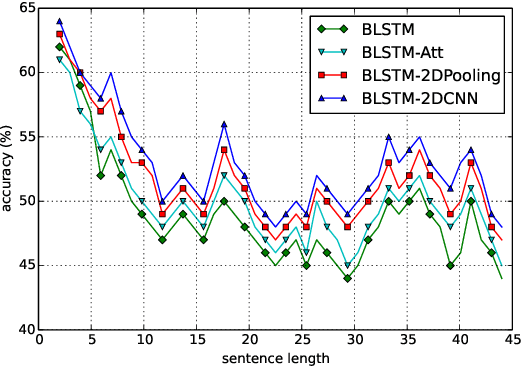
Recurrent Neural Network (RNN) is one of the most popular architectures used in Natural Language Processsing (NLP) tasks because its recurrent structure is very suitable to process variable-length text. RNN can utilize distributed representations of words by first converting the tokens comprising each text into vectors, which form a matrix. And this matrix includes two dimensions: the time-step dimension and the feature vector dimension. Then most existing models usually utilize one-dimensional (1D) max pooling operation or attention-based operation only on the time-step dimension to obtain a fixed-length vector. However, the features on the feature vector dimension are not mutually independent, and simply applying 1D pooling operation over the time-step dimension independently may destroy the structure of the feature representation. On the other hand, applying two-dimensional (2D) pooling operation over the two dimensions may sample more meaningful features for sequence modeling tasks. To integrate the features on both dimensions of the matrix, this paper explores applying 2D max pooling operation to obtain a fixed-length representation of the text. This paper also utilizes 2D convolution to sample more meaningful information of the matrix. Experiments are conducted on six text classification tasks, including sentiment analysis, question classification, subjectivity classification and newsgroup classification. Compared with the state-of-the-art models, the proposed models achieve excellent performance on 4 out of 6 tasks. Specifically, one of the proposed models achieves highest accuracy on Stanford Sentiment Treebank binary classification and fine-grained classification tasks.