Horizon-free Reinforcement Learning in Adversarial Linear Mixture MDPs

Recent studies have shown that episodic reinforcement learning (RL) is no harder than bandits when the total reward is bounded by $1$, and proved regret bounds that have a polylogarithmic dependence on the planning horizon $H$. However, it remains an open question that if such results can be carried over to adversarial RL, where the reward is adversarially chosen at each episode. In this paper, we answer this question affirmatively by proposing the first horizon-free policy search algorithm. To tackle the challenges caused by exploration and adversarially chosen reward, our algorithm employs (1) a variance-uncertainty-aware weighted least square estimator for the transition kernel; and (2) an occupancy measure-based technique for the online search of a \emph{stochastic} policy. We show that our algorithm achieves an $\tilde{O}\big((d+\log (|\mathcal{S}|^2 |\mathcal{A}|))\sqrt{K}\big)$ regret with full-information feedback, where $d$ is the dimension of a known feature mapping linearly parametrizing the unknown transition kernel of the MDP, $K$ is the number of episodes, $|\mathcal{S}|$ and $|\mathcal{A}|$ are the cardinalities of the state and action spaces. We also provide hardness results and regret lower bounds to justify the near optimality of our algorithm and the unavoidability of $\log|\mathcal{S}|$ and $\log|\mathcal{A}|$ in the regret bound.

Cooperative Multi-Agent Reinforcement Learning: Asynchronous Communication and Linear Function Approximation

We study multi-agent reinforcement learning in the setting of episodic Markov decision processes, where multiple agents cooperate via communication through a central server. We propose a provably efficient algorithm based on value iteration that enable asynchronous communication while ensuring the advantage of cooperation with low communication overhead. With linear function approximation, we prove that our algorithm enjoys an $\tilde{\mathcal{O}}(d^{3/2}H^2\sqrt{K})$ regret with $\tilde{\mathcal{O}}(dHM^2)$ communication complexity, where $d$ is the feature dimension, $H$ is the horizon length, $M$ is the total number of agents, and $K$ is the total number of episodes. We also provide a lower bound showing that a minimal $\Omega(dM)$ communication complexity is required to improve the performance through collaboration.

On the Interplay Between Misspecification and Sub-optimality Gap in Linear Contextual Bandits

We study linear contextual bandits in the misspecified setting, where the expected reward function can be approximated by a linear function class up to a bounded misspecification level $\zeta>0$. We propose an algorithm based on a novel data selection scheme, which only selects the contextual vectors with large uncertainty for online regression. We show that, when the misspecification level $\zeta$ is dominated by $\tilde O (\Delta / \sqrt{d})$ with $\Delta$ being the minimal sub-optimality gap and $d$ being the dimension of the contextual vectors, our algorithm enjoys the same gap-dependent regret bound $\tilde O (d^2/\Delta)$ as in the well-specified setting up to logarithmic factors. In addition, we show that an existing algorithm SupLinUCB (Chu et al., 2011) can also achieve a gap-dependent constant regret bound without the knowledge of sub-optimality gap $\Delta$. Together with a lower bound adapted from Lattimore et al. (2020), our result suggests an interplay between misspecification level and the sub-optimality gap: (1) the linear contextual bandit model is efficiently learnable when $\zeta \leq \tilde O(\Delta / \sqrt{d})$; and (2) it is not efficiently learnable when $\zeta \geq \tilde \Omega({\Delta} / {\sqrt{d}})$. Experiments on both synthetic and real-world datasets corroborate our theoretical results.

Variance-Dependent Regret Bounds for Linear Bandits and Reinforcement Learning: Adaptivity and Computational Efficiency

Recently, several studies (Zhou et al., 2021a; Zhang et al., 2021b; Kim et al., 2021; Zhou and Gu, 2022) have provided variance-dependent regret bounds for linear contextual bandits, which interpolates the regret for the worst-case regime and the deterministic reward regime. However, these algorithms are either computationally intractable or unable to handle unknown variance of the noise. In this paper, we present a novel solution to this open problem by proposing the first computationally efficient algorithm for linear bandits with heteroscedastic noise. Our algorithm is adaptive to the unknown variance of noise and achieves an $\tilde{O}(d \sqrt{\sum_{k = 1}^K \sigma_k^2} + d)$ regret, where $\sigma_k^2$ is the variance of the noise at the round $k$, $d$ is the dimension of the contexts and $K$ is the total number of rounds. Our results are based on an adaptive variance-aware confidence set enabled by a new Freedman-type concentration inequality for self-normalized martingales and a multi-layer structure to stratify the context vectors into different layers with different uniform upper bounds on the uncertainty. Furthermore, our approach can be extended to linear mixture Markov decision processes (MDPs) in reinforcement learning. We propose a variance-adaptive algorithm for linear mixture MDPs, which achieves a problem-dependent horizon-free regret bound that can gracefully reduce to a nearly constant regret for deterministic MDPs. Unlike existing nearly minimax optimal algorithms for linear mixture MDPs, our algorithm does not require explicit variance estimation of the transitional probabilities or the use of high-order moment estimators to attain horizon-free regret. We believe the techniques developed in this paper can have independent value for general online decision making problems.

Nearly Minimax Optimal Reinforcement Learning for Linear Markov Decision Processes

We study reinforcement learning (RL) with linear function approximation. For episodic time-inhomogeneous linear Markov decision processes (linear MDPs) whose transition dynamic can be parameterized as a linear function of a given feature mapping, we propose the first computationally efficient algorithm that achieves the nearly minimax optimal regret $\tilde O(d\sqrt{H^3K})$, where $d$ is the dimension of the feature mapping, $H$ is the planning horizon, and $K$ is the number of episodes. Our algorithm is based on a weighted linear regression scheme with a carefully designed weight, which depends on a new variance estimator that (1) directly estimates the variance of the \emph{optimal} value function, (2) monotonically decreases with respect to the number of episodes to ensure a better estimation accuracy, and (3) uses a rare-switching policy to update the value function estimator to control the complexity of the estimated value function class. Our work provides a complete answer to optimal RL with linear MDPs, and the developed algorithm and theoretical tools may be of independent interest.

A Simple and Provably Efficient Algorithm for Asynchronous Federated Contextual Linear Bandits

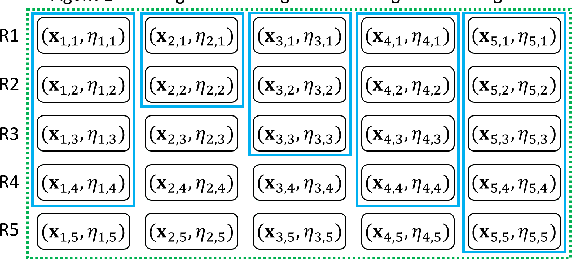
We study federated contextual linear bandits, where $M$ agents cooperate with each other to solve a global contextual linear bandit problem with the help of a central server. We consider the asynchronous setting, where all agents work independently and the communication between one agent and the server will not trigger other agents' communication. We propose a simple algorithm named \texttt{FedLinUCB} based on the principle of optimism. We prove that the regret of \texttt{FedLinUCB} is bounded by $\tilde{O}(d\sqrt{\sum_{m=1}^M T_m})$ and the communication complexity is $\tilde{O}(dM^2)$, where $d$ is the dimension of the contextual vector and $T_m$ is the total number of interactions with the environment by $m$-th agent. To the best of our knowledge, this is the first provably efficient algorithm that allows fully asynchronous communication for federated contextual linear bandits, while achieving the same regret guarantee as in the single-agent setting.

Nearly Optimal Algorithms for Linear Contextual Bandits with Adversarial Corruptions

We study the linear contextual bandit problem in the presence of adversarial corruption, where the reward at each round is corrupted by an adversary, and the corruption level (i.e., the sum of corruption magnitudes over the horizon) is $C\geq 0$. The best-known algorithms in this setting are limited in that they either are computationally inefficient or require a strong assumption on the corruption, or their regret is at least $C$ times worse than the regret without corruption. In this paper, to overcome these limitations, we propose a new algorithm based on the principle of optimism in the face of uncertainty. At the core of our algorithm is a weighted ridge regression where the weight of each chosen action depends on its confidence up to some threshold. We show that for both known $C$ and unknown $C$ cases, our algorithm with proper choice of hyperparameter achieves a regret that nearly matches the lower bounds. Thus, our algorithm is nearly optimal up to logarithmic factors for both cases. Notably, our algorithm achieves the near-optimal regret for both corrupted and uncorrupted cases ($C=0$) simultaneously.

Bandit Learning with General Function Classes: Heteroscedastic Noise and Variance-dependent Regret Bounds

We consider learning a stochastic bandit model, where the reward function belongs to a general class of uniformly bounded functions, and the additive noise can be heteroscedastic. Our model captures contextual linear bandits and generalized linear bandits as special cases. While previous works (Kirschner and Krause, 2018; Zhou et al., 2021) based on weighted ridge regression can deal with linear bandits with heteroscedastic noise, they are not directly applicable to our general model due to the curse of nonlinearity. In order to tackle this problem, we propose a multi-level learning framework for the general bandit model. The core idea of our framework is to partition the observed data into different levels according to the variance of their respective reward and perform online learning at each level collaboratively. Under our framework, we first design an algorithm that constructs the variance-aware confidence set based on empirical risk minimization and prove a variance-dependent regret bound. For generalized linear bandits, we further propose an algorithm based on follow-the-regularized-leader (FTRL) subroutine and online-to-confidence-set conversion, which can achieve a tighter variance-dependent regret under certain conditions.

Learning Stochastic Shortest Path with Linear Function Approximation

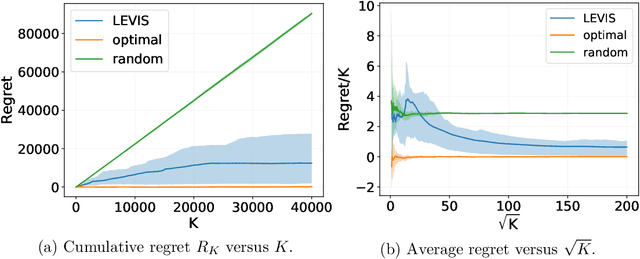
We study the stochastic shortest path (SSP) problem in reinforcement learning with linear function approximation, where the transition kernel is represented as a linear mixture of unknown models. We call this class of SSP problems the linear mixture SSP. We propose a novel algorithm for learning the linear mixture SSP, which can attain a $\tilde O(d B_{\star}^{1.5}\sqrt{K/c_{\min}})$ regret. Here $K$ is the number of episodes, $d$ is the dimension of the feature mapping in the mixture model, $B_{\star}$ bounds the expected cumulative cost of the optimal policy, and $c_{\min}>0$ is the lower bound of the cost function. Our algorithm also applies to the case when $c_{\min} = 0$, where a $\tilde O(K^{2/3})$ regret is guaranteed. To the best of our knowledge, this is the first algorithm with a sublinear regret guarantee for learning linear mixture SSP. In complement to the regret upper bounds, we also prove a lower bound of $\Omega(d B_{\star} \sqrt{K})$, which nearly matches our upper bound.

Locally Differentially Private Reinforcement Learning for Linear Mixture Markov Decision Processes

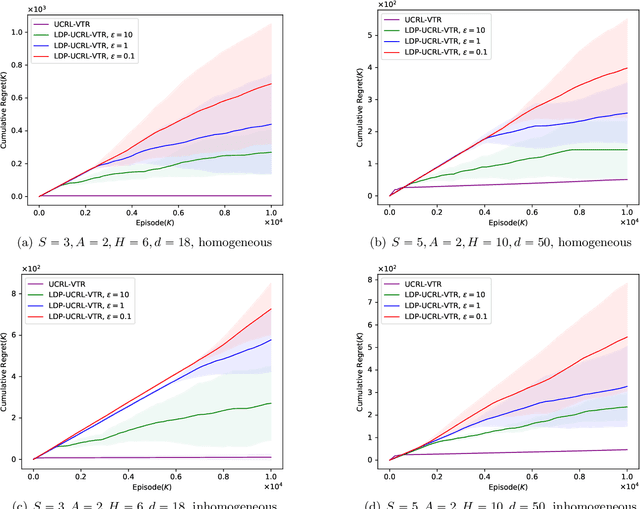
Reinforcement learning (RL) algorithms can be used to provide personalized services, which rely on users' private and sensitive data. To protect the users' privacy, privacy-preserving RL algorithms are in demand. In this paper, we study RL with linear function approximation and local differential privacy (LDP) guarantees. We propose a novel $(\varepsilon, \delta)$-LDP algorithm for learning a class of Markov decision processes (MDPs) dubbed linear mixture MDPs, and obtains an $\tilde{\mathcal{O}}( d^{5/4}H^{7/4}T^{3/4}\left(\log(1/\delta)\right)^{1/4}\sqrt{1/\varepsilon})$ regret, where $d$ is the dimension of feature mapping, $H$ is the length of the planning horizon, and $T$ is the number of interactions with the environment. We also prove a lower bound $\Omega(dH\sqrt{T}/\left(e^{\varepsilon}(e^{\varepsilon}-1)\right))$ for learning linear mixture MDPs under $\varepsilon$-LDP constraint. Experiments on synthetic datasets verify the effectiveness of our algorithm. To the best of our knowledge, this is the first provable privacy-preserving RL algorithm with linear function approximation.