Assessing Episodic Memory in LLMs with Sequence Order Recall Tasks

Current LLM benchmarks focus on evaluating models' memory of facts and semantic relations, primarily assessing semantic aspects of long-term memory. However, in humans, long-term memory also includes episodic memory, which links memories to their contexts, such as the time and place they occurred. The ability to contextualize memories is crucial for many cognitive tasks and everyday functions. This form of memory has not been evaluated in LLMs with existing benchmarks. To address the gap in evaluating memory in LLMs, we introduce Sequence Order Recall Tasks (SORT), which we adapt from tasks used to study episodic memory in cognitive psychology. SORT requires LLMs to recall the correct order of text segments, and provides a general framework that is both easily extendable and does not require any additional annotations. We present an initial evaluation dataset, Book-SORT, comprising 36k pairs of segments extracted from 9 books recently added to the public domain. Based on a human experiment with 155 participants, we show that humans can recall sequence order based on long-term memory of a book. We find that models can perform the task with high accuracy when relevant text is given in-context during the SORT evaluation. However, when presented with the book text only during training, LLMs' performance on SORT falls short. By allowing to evaluate more aspects of memory, we believe that SORT will aid in the emerging development of memory-augmented models.

Slower is Better: Revisiting the Forgetting Mechanism in LSTM for Slower Information Decay

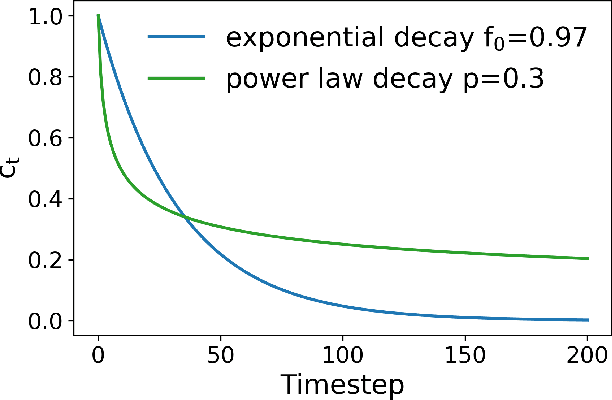
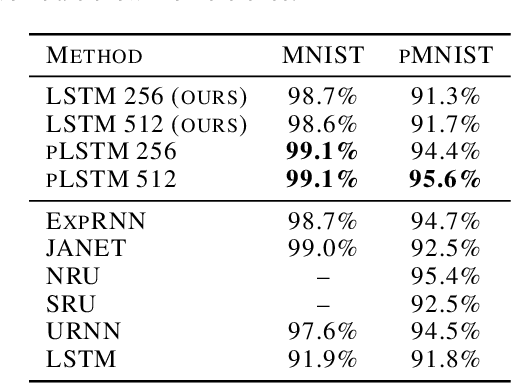
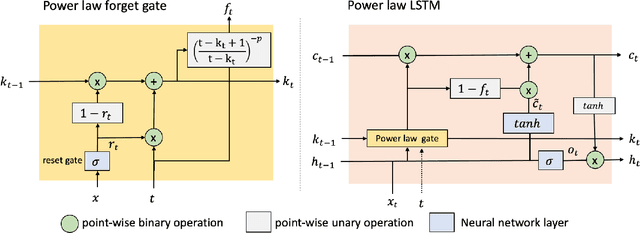
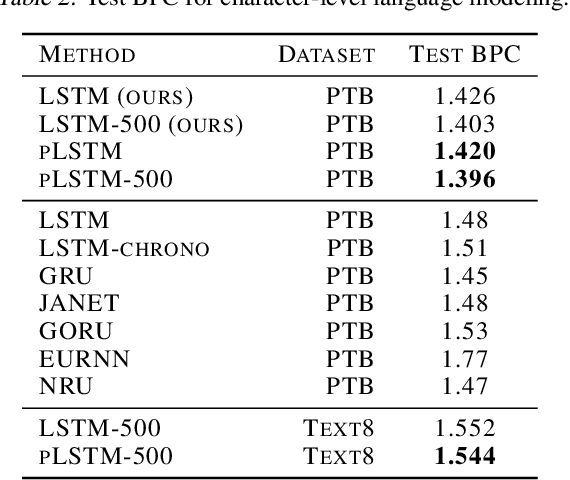
Sequential information contains short- to long-range dependencies; however, learning long-timescale information has been a challenge for recurrent neural networks. Despite improvements in long short-term memory networks (LSTMs), the forgetting mechanism results in the exponential decay of information, limiting their capacity to capture long-timescale information. Here, we propose a power law forget gate, which instead learns to forget information along a slower power law decay function. Specifically, the new gate learns to control the power law decay factor, p, allowing the network to adjust the information decay rate according to task demands. Our experiments show that an LSTM with power law forget gates (pLSTM) can effectively capture long-range dependencies beyond hundreds of elements on image classification, language modeling, and categorization tasks, improving performance over the vanilla LSTM. We also inspected the revised forget gate by varying the initialization of p, setting p to a fixed value, and ablating cells in the pLSTM network. The results show that the information decay can be controlled by the learnable decay factor p, which allows pLSTM to achieve its superior performance. Altogether, we found that LSTM with the proposed forget gate can learn long-term dependencies, outperforming other recurrent networks in multiple domains; such gating mechanism can be integrated into other architectures for improving the learning of long timescale information in recurrent neural networks.

Multi-timescale representation learning in LSTM Language Models

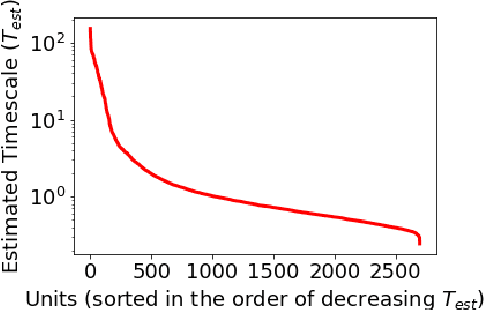
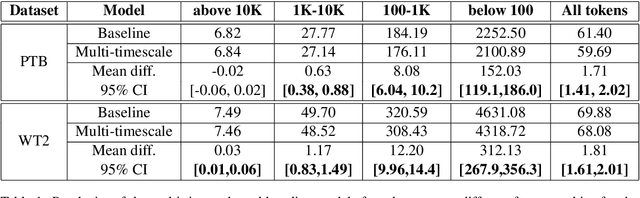
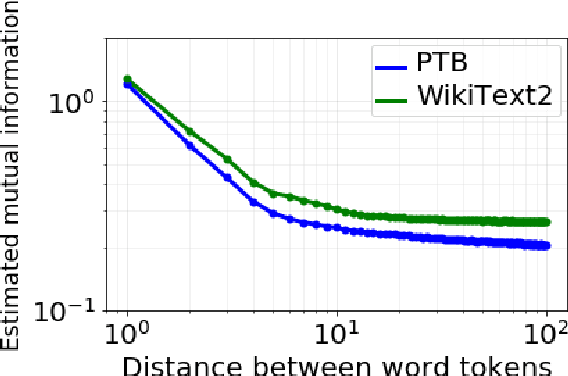
Although neural language models are effective at capturing statistics of natural language, their representations are challenging to interpret. In particular, it is unclear how these models retain information over multiple timescales. In this work, we construct explicitly multi-timescale language models by manipulating the input and forget gate biases in a long short-term memory (LSTM) network. The distribution of timescales is selected to approximate power law statistics of natural language through a combination of exponentially decaying memory cells. We then empirically analyze the timescale of information routed through each part of the model using word ablation experiments and forget gate visualizations. These experiments show that the multi-timescale model successfully learns representations at the desired timescales, and that the distribution includes longer timescales than a standard LSTM. Further, information about high-,mid-, and low-frequency words is routed preferentially through units with the appropriate timescales. Thus we show how to construct language models with interpretable representations of different information timescales.

A single-layer RNN can approximate stacked and bidirectional RNNs, and topologies in between

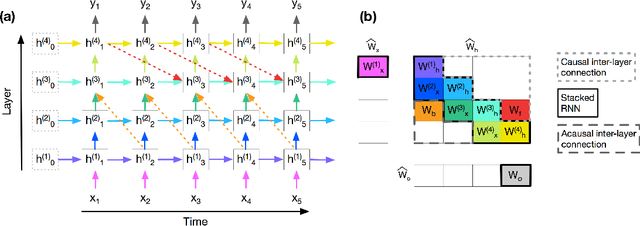
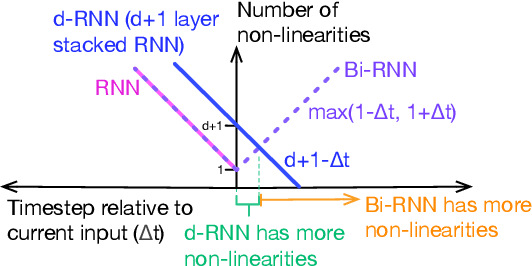
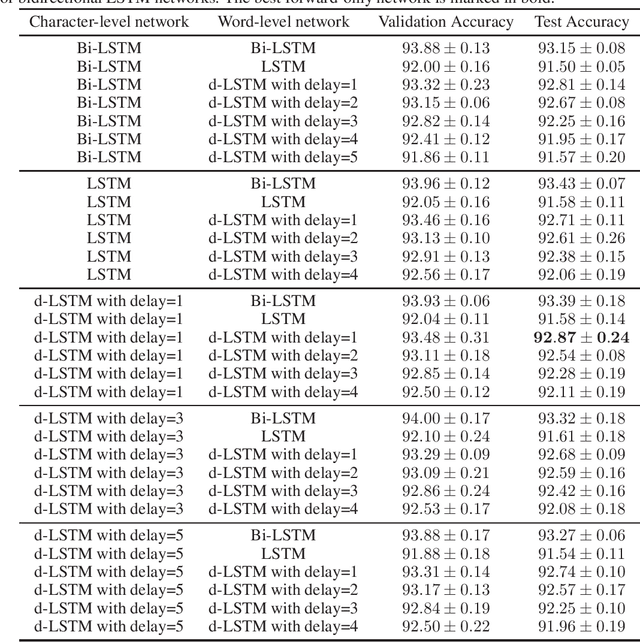
To enhance the expressiveness and representational capacity of recurrent neural networks (RNN), a large body of work has emerged exploring stacked architectures with additional topological modifications like shortcut connections or bidirectionality. However, choosing the best network for a particular problem requires a combinatorial search over architectures and their hyperparameters. In this work, we show that a single-layer RNN can perfectly mimic an arbitrarily deep stacked RNN under specific constraints on its weight matrix and a delay between input and output. This obviates the need to manually select hyperparameters like the number of layers. Additionally, we show that weakening weight constraints while keeping the delay gives rise to partial acausality in the single-layer RNN, much like a bidirectional network. Synthetic experiments confirm that the delayed RNN can mimic bidirectional networks in perfectly solving some acausal tasks, outperforming them in others. Finally, we show that in a challenging language processing task, the delayed RNN performs within 0.3\% of the accuracy of the bidirectional network while reducing computational costs.

Clinically Deployed Distributed Magnetic Resonance Imaging Reconstruction: Application to Pediatric Knee Imaging

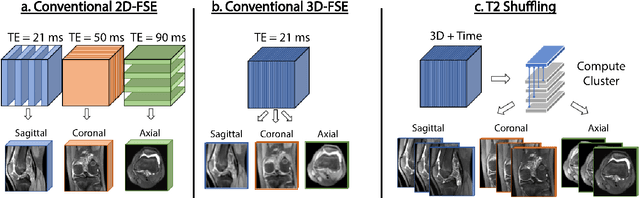
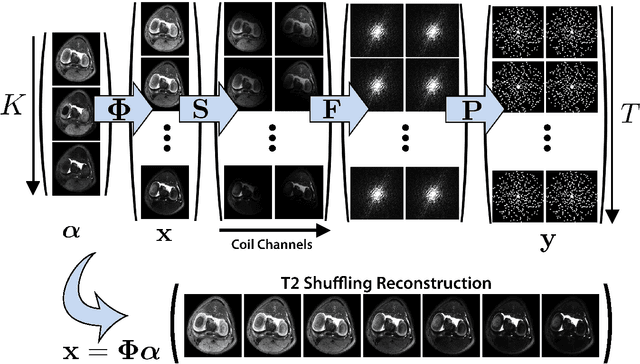
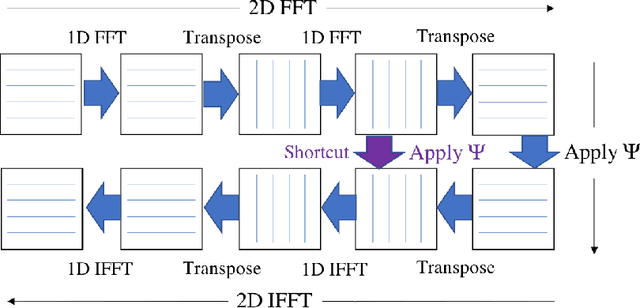
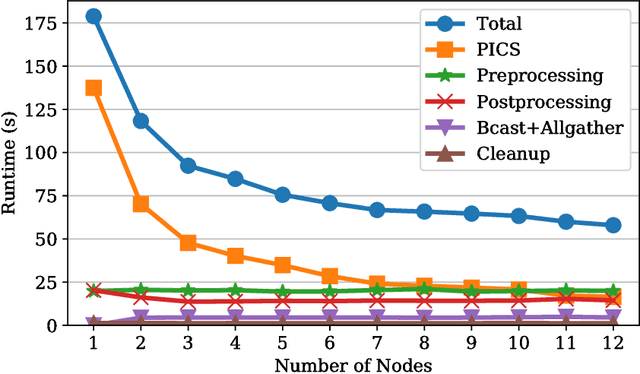
Magnetic resonance imaging is capable of producing volumetric images without ionizing radiation. Nonetheless, long acquisitions lead to prohibitively long exams. Compressed sensing (CS) can enable faster scanning via sub-sampling with reduced artifacts. However, CS requires significantly higher reconstruction computation, limiting current clinical applications to 2D/3D or limited-resolution dynamic imaging. Here we analyze the practical limitations to T2 Shuffling, a four-dimensional CS-based acquisition, which provides sharp 3D-isotropic-resolution and multi-contrast images in a single scan. Our improvements to the pipeline on a single machine provide a 3x overall reconstruction speedup, which allowed us to add algorithmic changes improving image quality. Using four machines, we achieved additional 2.1x improvement through distributed parallelization. Our solution reduced the reconstruction time in the hospital to 90 seconds on a 4-node cluster, enabling its use clinically. To understand the implications of scaling this application, we simulated running our reconstructions with a multiple scanner setup typical in hospitals.

Efficient, sparse representation of manifold distance matrices for classical scaling

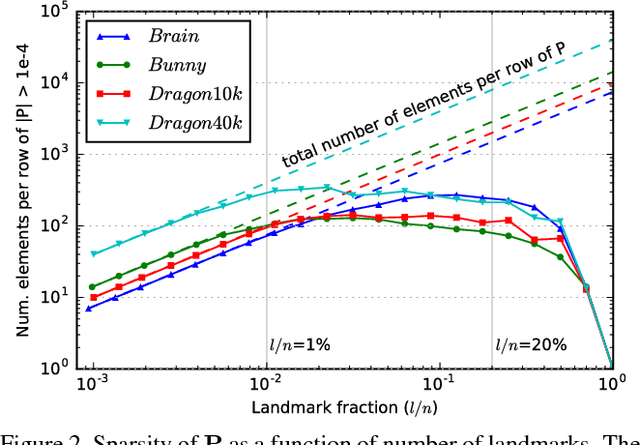
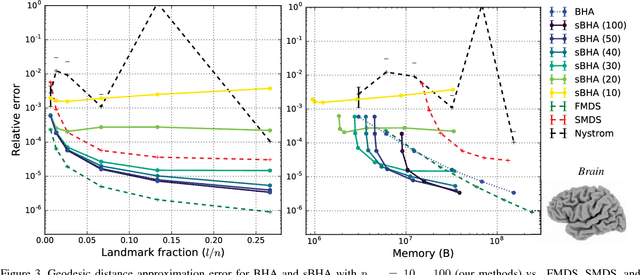
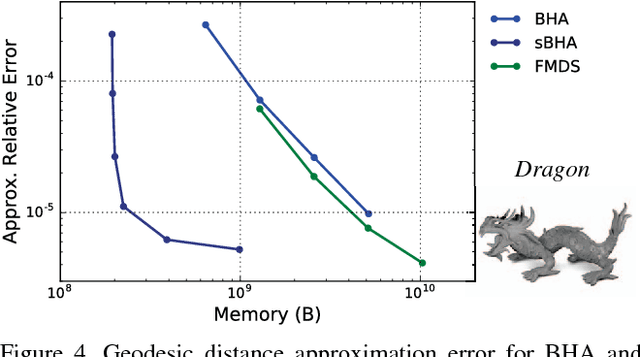
Geodesic distance matrices can reveal shape properties that are largely invariant to non-rigid deformations, and thus are often used to analyze and represent 3-D shapes. However, these matrices grow quadratically with the number of points. Thus for large point sets it is common to use a low-rank approximation to the distance matrix, which fits in memory and can be efficiently analyzed using methods such as multidimensional scaling (MDS). In this paper we present a novel sparse method for efficiently representing geodesic distance matrices using biharmonic interpolation. This method exploits knowledge of the data manifold to learn a sparse interpolation operator that approximates distances using a subset of points. We show that our method is 2x faster and uses 20x less memory than current leading methods for solving MDS on large point sets, with similar quality. This enables analyses of large point sets that were previously infeasible.

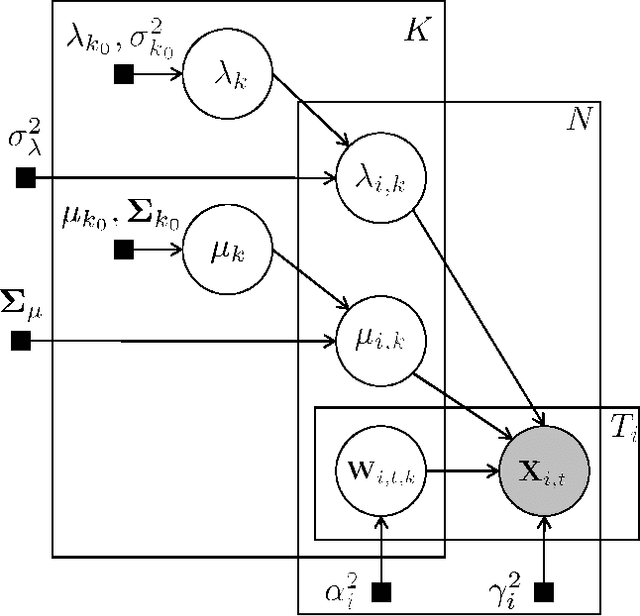
A Searchlight Factor Model Approach for Locating Shared Information in Multi-Subject fMRI Analysis

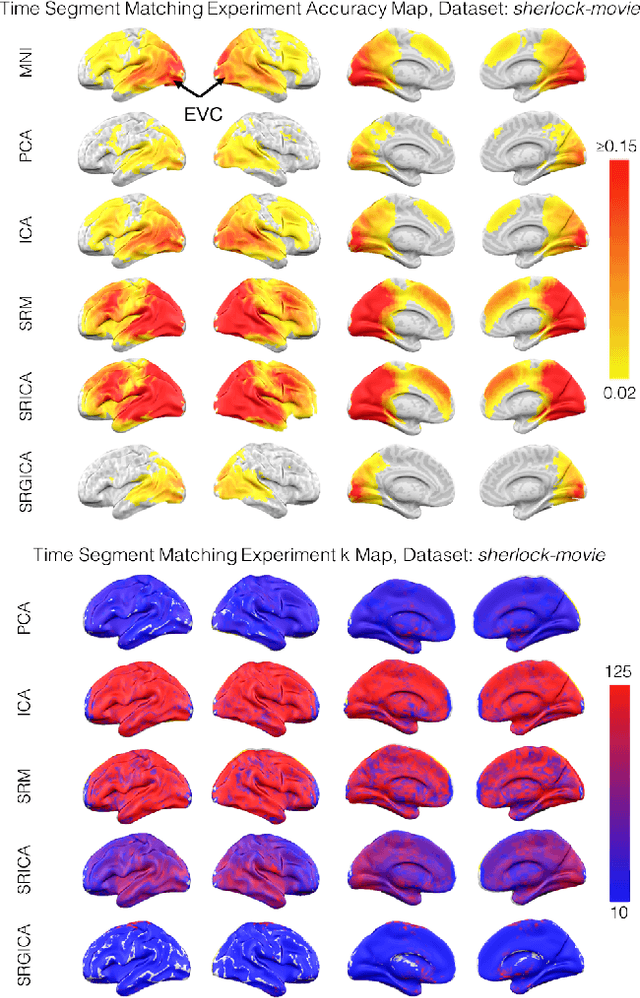
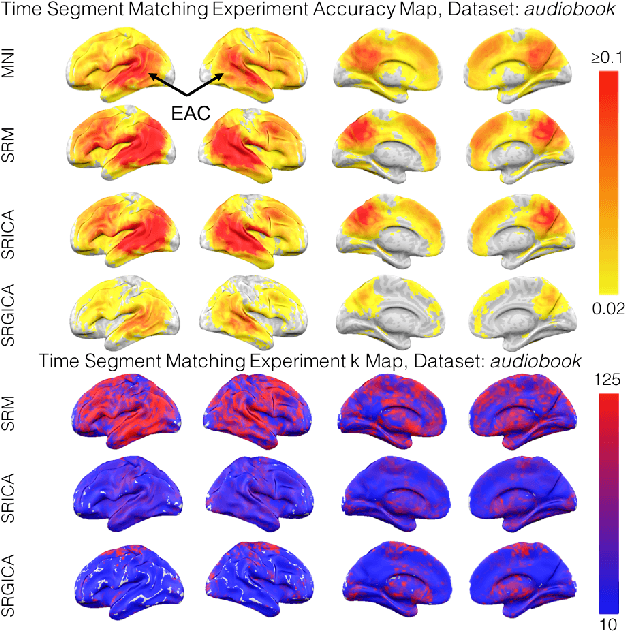
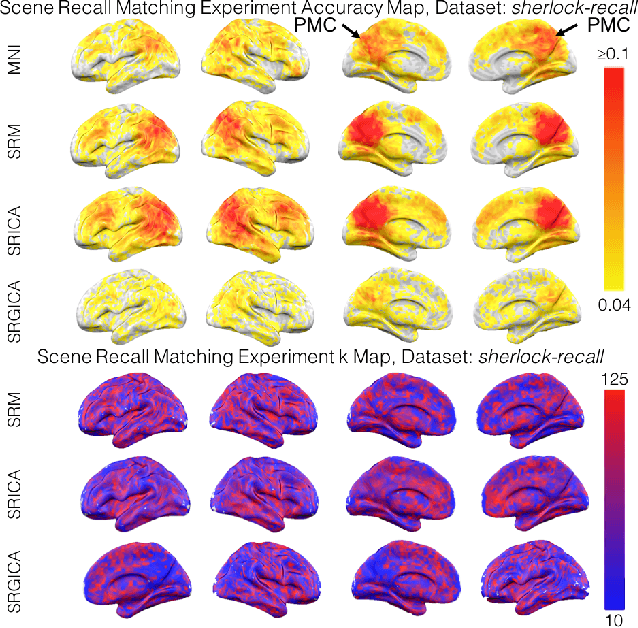
There is a growing interest in joint multi-subject fMRI analysis. The challenge of such analysis comes from inherent anatomical and functional variability across subjects. One approach to resolving this is a shared response factor model. This assumes a shared and time synchronized stimulus across subjects. Such a model can often identify shared information, but it may not be able to pinpoint with high resolution the spatial location of this information. In this work, we examine a searchlight based shared response model to identify shared information in small contiguous regions (searchlights) across the whole brain. Validation using classification tasks demonstrates that we can pinpoint informative local regions.

Enabling Factor Analysis on Thousand-Subject Neuroimaging Datasets

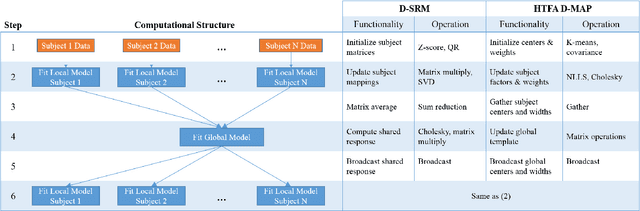
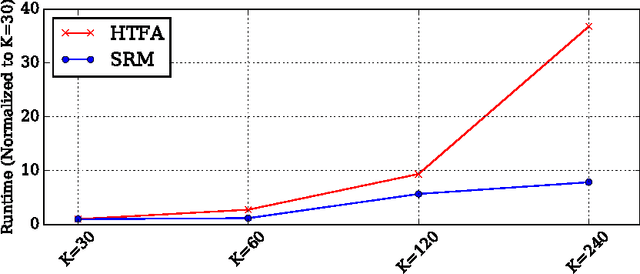
The scale of functional magnetic resonance image data is rapidly increasing as large multi-subject datasets are becoming widely available and high-resolution scanners are adopted. The inherent low-dimensionality of the information in this data has led neuroscientists to consider factor analysis methods to extract and analyze the underlying brain activity. In this work, we consider two recent multi-subject factor analysis methods: the Shared Response Model and Hierarchical Topographic Factor Analysis. We perform analytical, algorithmic, and code optimization to enable multi-node parallel implementations to scale. Single-node improvements result in 99x and 1812x speedups on these two methods, and enables the processing of larger datasets. Our distributed implementations show strong scaling of 3.3x and 5.5x respectively with 20 nodes on real datasets. We also demonstrate weak scaling on a synthetic dataset with 1024 subjects, on up to 1024 nodes and 32,768 cores.

A Convolutional Autoencoder for Multi-Subject fMRI Data Aggregation

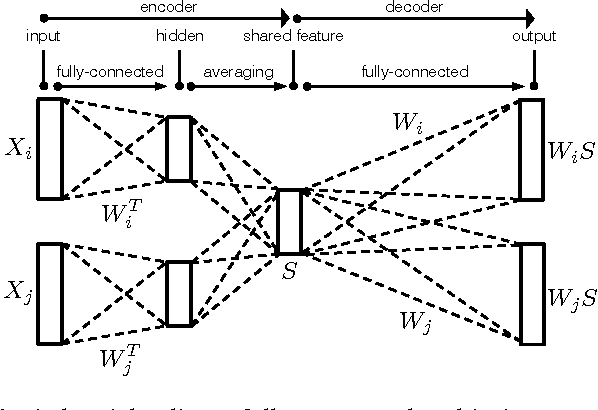
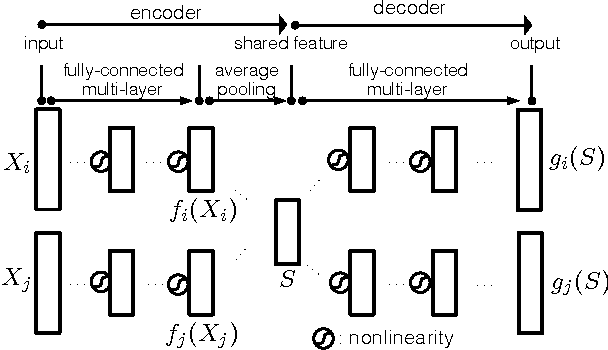
Finding the most effective way to aggregate multi-subject fMRI data is a long-standing and challenging problem. It is of increasing interest in contemporary fMRI studies of human cognition due to the scarcity of data per subject and the variability of brain anatomy and functional response across subjects. Recent work on latent factor models shows promising results in this task but this approach does not preserve spatial locality in the brain. We examine two ways to combine the ideas of a factor model and a searchlight based analysis to aggregate multi-subject fMRI data while preserving spatial locality. We first do this directly by combining a recent factor method known as a shared response model with searchlight analysis. Then we design a multi-view convolutional autoencoder for the same task. Both approaches preserve spatial locality and have competitive or better performance compared with standard searchlight analysis and the shared response model applied across the whole brain. We also report a system design to handle the computational challenge of training the convolutional autoencoder.

A multilevel framework for sparse optimization with application to inverse covariance estimation and logistic regression

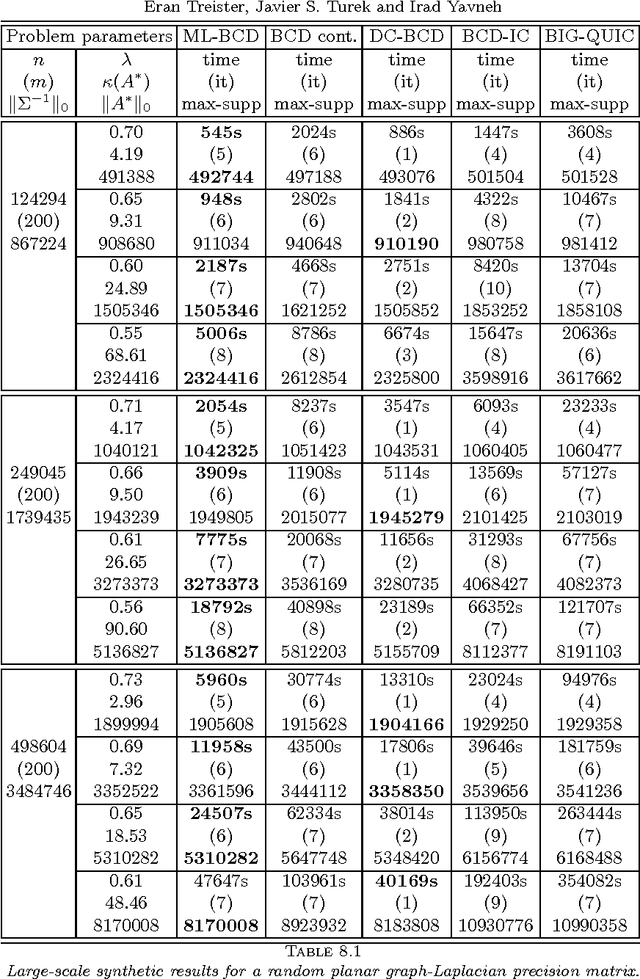
Solving l1 regularized optimization problems is common in the fields of computational biology, signal processing and machine learning. Such l1 regularization is utilized to find sparse minimizers of convex functions. A well-known example is the LASSO problem, where the l1 norm regularizes a quadratic function. A multilevel framework is presented for solving such l1 regularized sparse optimization problems efficiently. We take advantage of the expected sparseness of the solution, and create a hierarchy of problems of similar type, which is traversed in order to accelerate the optimization process. This framework is applied for solving two problems: (1) the sparse inverse covariance estimation problem, and (2) l1-regularized logistic regression. In the first problem, the inverse of an unknown covariance matrix of a multivariate normal distribution is estimated, under the assumption that it is sparse. To this end, an l1 regularized log-determinant optimization problem needs to be solved. This task is challenging especially for large-scale datasets, due to time and memory limitations. In the second problem, the l1-regularization is added to the logistic regression classification objective to reduce overfitting to the data and obtain a sparse model. Numerical experiments demonstrate the efficiency of the multilevel framework in accelerating existing iterative solvers for both of these problems.