StepProof: Step-by-step verification of natural language mathematical proofs

Interactive theorem provers (ITPs) are powerful tools for the formal verification of mathematical proofs down to the axiom level. However, their lack of a natural language interface remains a significant limitation. Recent advancements in large language models (LLMs) have enhanced the understanding of natural language inputs, paving the way for autoformalization - the process of translating natural language proofs into formal proofs that can be verified. Despite these advancements, existing autoformalization approaches are limited to verifying complete proofs and lack the capability for finer, sentence-level verification. To address this gap, we propose StepProof, a novel autoformalization method designed for granular, step-by-step verification. StepProof breaks down complete proofs into multiple verifiable subproofs, enabling sentence-level verification. Experimental results demonstrate that StepProof significantly improves proof success rates and efficiency compared to traditional methods. Additionally, we found that minor manual adjustments to the natural language proofs, tailoring them for step-level verification, further enhanced StepProof's performance in autoformalization.

When fractional quasi p-norms concentrate

Concentration of distances in high dimension is an important factor for the development and design of stable and reliable data analysis algorithms. In this paper, we address the fundamental long-standing question about the concentration of distances in high dimension for fractional quasi $p$-norms, $p\in(0,1)$. The topic has been at the centre of various theoretical and empirical controversies. Here we, for the first time, identify conditions when fractional quasi $p$-norms concentrate and when they don't. We show that contrary to some earlier suggestions, for broad classes of distributions, fractional quasi $p$-norms admit exponential and uniform in $p$ concentration bounds. For these distributions, the results effectively rule out previously proposed approaches to alleviate concentration by "optimal" setting the values of $p$ in $(0,1)$. At the same time, we specify conditions and the corresponding families of distributions for which one can still control concentration rates by appropriate choices of $p$. We also show that in an arbitrarily small vicinity of a distribution from a large class of distributions for which uniform concentration occurs, there are uncountably many other distributions featuring anti-concentration properties. Importantly, this behavior enables devising relevant data encoding or representation schemes favouring or discouraging distance concentration. The results shed new light on this long-standing problem and resolve the tension around the topic in both theory and empirical evidence reported in the literature.

Stealth edits for provably fixing or attacking large language models

We reveal new methods and the theoretical foundations of techniques for editing large language models. We also show how the new theory can be used to assess the editability of models and to expose their susceptibility to previously unknown malicious attacks. Our theoretical approach shows that a single metric (a specific measure of the intrinsic dimensionality of the model's features) is fundamental to predicting the success of popular editing approaches, and reveals new bridges between disparate families of editing methods. We collectively refer to these approaches as stealth editing methods, because they aim to directly and inexpensively update a model's weights to correct the model's responses to known hallucinating prompts without otherwise affecting the model's behaviour, without requiring retraining. By carefully applying the insight gleaned from our theoretical investigation, we are able to introduce a new network block -- named a jet-pack block -- which is optimised for highly selective model editing, uses only standard network operations, and can be inserted into existing networks. The intrinsic dimensionality metric also determines the vulnerability of a language model to a stealth attack: a small change to a model's weights which changes its response to a single attacker-chosen prompt. Stealth attacks do not require access to or knowledge of the model's training data, therefore representing a potent yet previously unrecognised threat to redistributed foundation models. They are computationally simple enough to be implemented in malware in many cases. Extensive experimental results illustrate and support the method and its theoretical underpinnings. Demos and source code for editing language models are available at https://github.com/qinghua-zhou/stealth-edits.

Weakly Supervised Learners for Correction of AI Errors with Provable Performance Guarantees

We present a new methodology for handling AI errors by introducing weakly supervised AI error correctors with a priori performance guarantees. These AI correctors are auxiliary maps whose role is to moderate the decisions of some previously constructed underlying classifier by either approving or rejecting its decisions. The rejection of a decision can be used as a signal to suggest abstaining from making a decision. A key technical focus of the work is in providing performance guarantees for these new AI correctors through bounds on the probabilities of incorrect decisions. These bounds are distribution agnostic and do not rely on assumptions on the data dimension. Our empirical example illustrates how the framework can be applied to improve the performance of an image classifier in a challenging real-world task where training data are scarce.

The Boundaries of Verifiable Accuracy, Robustness, and Generalisation in Deep Learning

In this work, we assess the theoretical limitations of determining guaranteed stability and accuracy of neural networks in classification tasks. We consider classical distribution-agnostic framework and algorithms minimising empirical risks and potentially subjected to some weights regularisation. We show that there is a large family of tasks for which computing and verifying ideal stable and accurate neural networks in the above settings is extremely challenging, if at all possible, even when such ideal solutions exist within the given class of neural architectures.

How adversarial attacks can disrupt seemingly stable accurate classifiers

Adversarial attacks dramatically change the output of an otherwise accurate learning system using a seemingly inconsequential modification to a piece of input data. Paradoxically, empirical evidence indicates that even systems which are robust to large random perturbations of the input data remain susceptible to small, easily constructed, adversarial perturbations of their inputs. Here, we show that this may be seen as a fundamental feature of classifiers working with high dimensional input data. We introduce a simple generic and generalisable framework for which key behaviours observed in practical systems arise with high probability -- notably the simultaneous susceptibility of the (otherwise accurate) model to easily constructed adversarial attacks, and robustness to random perturbations of the input data. We confirm that the same phenomena are directly observed in practical neural networks trained on standard image classification problems, where even large additive random noise fails to trigger the adversarial instability of the network. A surprising takeaway is that even small margins separating a classifier's decision surface from training and testing data can hide adversarial susceptibility from being detected using randomly sampled perturbations. Counterintuitively, using additive noise during training or testing is therefore inefficient for eradicating or detecting adversarial examples, and more demanding adversarial training is required.

Agile gesture recognition for capacitive sensing devices: adapting on-the-job

Automated hand gesture recognition has been a focus of the AI community for decades. Traditionally, work in this domain revolved largely around scenarios assuming the availability of the flow of images of the user hands. This has partly been due to the prevalence of camera-based devices and the wide availability of image data. However, there is growing demand for gesture recognition technology that can be implemented on low-power devices using limited sensor data instead of high-dimensional inputs like hand images. In this work, we demonstrate a hand gesture recognition system and method that uses signals from capacitive sensors embedded into the etee hand controller. The controller generates real-time signals from each of the wearer five fingers. We use a machine learning technique to analyse the time series signals and identify three features that can represent 5 fingers within 500 ms. The analysis is composed of a two stage training strategy, including dimension reduction through principal component analysis and classification with K nearest neighbour. Remarkably, we found that this combination showed a level of performance which was comparable to more advanced methods such as supervised variational autoencoder. The base system can also be equipped with the capability to learn from occasional errors by providing it with an additional adaptive error correction mechanism. The results showed that the error corrector improve the classification performance in the base system without compromising its performance. The system requires no more than 1 ms of computing time per input sample, and is smaller than deep neural networks, demonstrating the feasibility of agile gesture recognition systems based on this technology.

Towards a mathematical understanding of learning from few examples with nonlinear feature maps

We consider the problem of data classification where the training set consists of just a few data points. We explore this phenomenon mathematically and reveal key relationships between the geometry of an AI model's feature space, the structure of the underlying data distributions, and the model's generalisation capabilities. The main thrust of our analysis is to reveal the influence on the model's generalisation capabilities of nonlinear feature transformations mapping the original data into high, and possibly infinite, dimensional spaces.

Learning from few examples with nonlinear feature maps

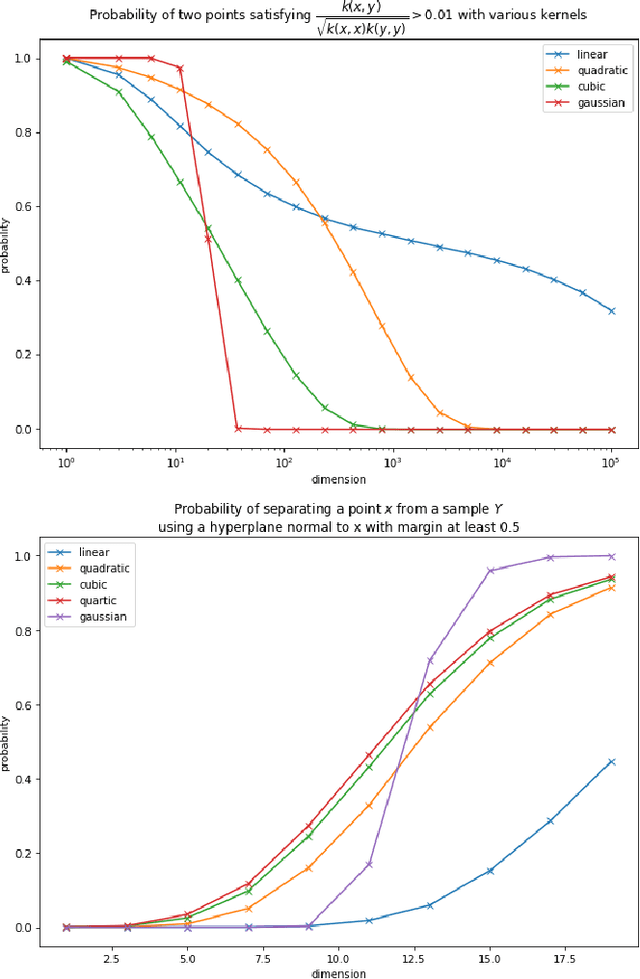
In this work we consider the problem of data classification in post-classical settings were the number of training examples consists of mere few data points. We explore the phenomenon and reveal key relationships between dimensionality of AI model's feature space, non-degeneracy of data distributions, and the model's generalisation capabilities. The main thrust of our present analysis is on the influence of nonlinear feature transformations mapping original data into higher- and possibly infinite-dimensional spaces on the resulting model's generalisation capabilities. Subject to appropriate assumptions, we establish new relationships between intrinsic dimensions of the transformed data and the probabilities to learn successfully from few presentations.

Quasi-orthogonality and intrinsic dimensions as measures of learning and generalisation

Finding best architectures of learning machines, such as deep neural networks, is a well-known technical and theoretical challenge. Recent work by Mellor et al (2021) showed that there may exist correlations between the accuracies of trained networks and the values of some easily computable measures defined on randomly initialised networks which may enable to search tens of thousands of neural architectures without training. Mellor et al used the Hamming distance evaluated over all ReLU neurons as such a measure. Motivated by these findings, in our work, we ask the question of the existence of other and perhaps more principled measures which could be used as determinants of success of a given neural architecture. In particular, we examine, if the dimensionality and quasi-orthogonality of neural networks' feature space could be correlated with the network's performance after training. We showed, using the setup as in Mellor et al, that dimensionality and quasi-orthogonality may jointly serve as network's performance discriminants. In addition to offering new opportunities to accelerate neural architecture search, our findings suggest important relationships between the networks' final performance and properties of their randomly initialised feature spaces: data dimension and quasi-orthogonality.