StepProof: Step-by-step verification of natural language mathematical proofs

Interactive theorem provers (ITPs) are powerful tools for the formal verification of mathematical proofs down to the axiom level. However, their lack of a natural language interface remains a significant limitation. Recent advancements in large language models (LLMs) have enhanced the understanding of natural language inputs, paving the way for autoformalization - the process of translating natural language proofs into formal proofs that can be verified. Despite these advancements, existing autoformalization approaches are limited to verifying complete proofs and lack the capability for finer, sentence-level verification. To address this gap, we propose StepProof, a novel autoformalization method designed for granular, step-by-step verification. StepProof breaks down complete proofs into multiple verifiable subproofs, enabling sentence-level verification. Experimental results demonstrate that StepProof significantly improves proof success rates and efficiency compared to traditional methods. Additionally, we found that minor manual adjustments to the natural language proofs, tailoring them for step-level verification, further enhanced StepProof's performance in autoformalization.

When fractional quasi p-norms concentrate

Concentration of distances in high dimension is an important factor for the development and design of stable and reliable data analysis algorithms. In this paper, we address the fundamental long-standing question about the concentration of distances in high dimension for fractional quasi $p$-norms, $p\in(0,1)$. The topic has been at the centre of various theoretical and empirical controversies. Here we, for the first time, identify conditions when fractional quasi $p$-norms concentrate and when they don't. We show that contrary to some earlier suggestions, for broad classes of distributions, fractional quasi $p$-norms admit exponential and uniform in $p$ concentration bounds. For these distributions, the results effectively rule out previously proposed approaches to alleviate concentration by "optimal" setting the values of $p$ in $(0,1)$. At the same time, we specify conditions and the corresponding families of distributions for which one can still control concentration rates by appropriate choices of $p$. We also show that in an arbitrarily small vicinity of a distribution from a large class of distributions for which uniform concentration occurs, there are uncountably many other distributions featuring anti-concentration properties. Importantly, this behavior enables devising relevant data encoding or representation schemes favouring or discouraging distance concentration. The results shed new light on this long-standing problem and resolve the tension around the topic in both theory and empirical evidence reported in the literature.

FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI

We introduce FrontierMath, a benchmark of hundreds of original, exceptionally challenging mathematics problems crafted and vetted by expert mathematicians. The questions cover most major branches of modern mathematics -- from computationally intensive problems in number theory and real analysis to abstract questions in algebraic geometry and category theory. Solving a typical problem requires multiple hours of effort from a researcher in the relevant branch of mathematics, and for the upper end questions, multiple days. FrontierMath uses new, unpublished problems and automated verification to reliably evaluate models while minimizing risk of data contamination. Current state-of-the-art AI models solve under 2% of problems, revealing a vast gap between AI capabilities and the prowess of the mathematical community. As AI systems advance toward expert-level mathematical abilities, FrontierMath offers a rigorous testbed that quantifies their progress.

High-dimensional separability for one- and few-shot learning

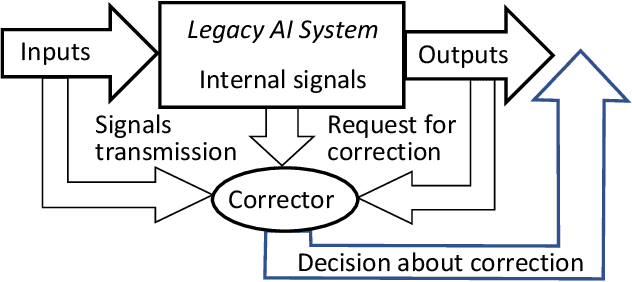
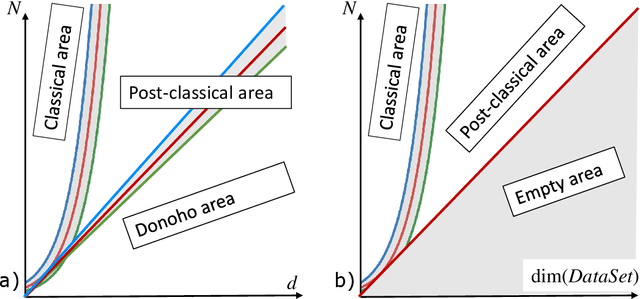
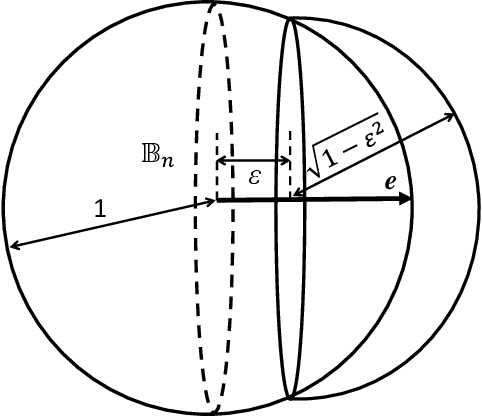
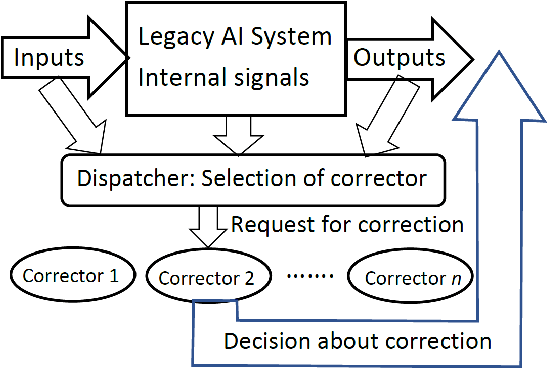
This work is driven by a practical question, corrections of Artificial Intelligence (AI) errors. Systematic re-training of a large AI system is hardly possible. To solve this problem, special external devices, correctors, are developed. They should provide quick and non-iterative system fix without modification of a legacy AI system. A common universal part of the AI corrector is a classifier that should separate undesired and erroneous behavior from normal operation. Training of such classifiers is a grand challenge at the heart of the one- and few-shot learning methods. Effectiveness of one- and few-short methods is based on either significant dimensionality reductions or the blessing of dimensionality effects. Stochastic separability is a blessing of dimensionality phenomenon that allows one-and few-shot error correction: in high-dimensional datasets under broad assumptions each point can be separated from the rest of the set by simple and robust linear discriminant. The hierarchical structure of data universe is introduced where each data cluster has a granular internal structure, etc. New stochastic separation theorems for the data distributions with fine-grained structure are formulated and proved. Separation theorems in infinite-dimensional limits are proven under assumptions of compact embedding of patterns into data space. New multi-correctors of AI systems are presented and illustrated with examples of predicting errors and learning new classes of objects by a deep convolutional neural network.

General stochastic separation theorems with optimal bounds

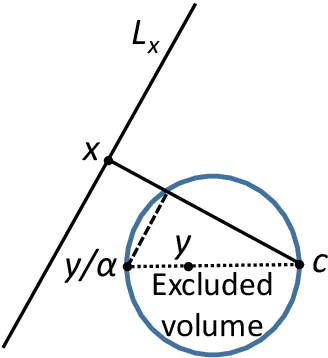
Phenomenon of stochastic separability was revealed and used in machine learning to correct errors of Artificial Intelligence (AI) systems and analyze AI instabilities. In high-dimensional datasets under broad assumptions each point can be separated from the rest of the set by simple and robust Fisher's discriminant (is Fisher separable). Errors or clusters of errors can be separated from the rest of the data. The ability to correct an AI system also opens up the possibility of an attack on it, and the high dimensionality induces vulnerabilities caused by the same stochastic separability that holds the keys to understanding the fundamentals of robustness and adaptivity in high-dimensional data-driven AI. To manage errors and analyze vulnerabilities, the stochastic separation theorems should evaluate the probability that the dataset will be Fisher separable in given dimensionality and for a given class of distributions. Explicit and optimal estimates of these separation probabilities are required, and this problem is solved in present work. The general stochastic separation theorems with optimal probability estimates are obtained for important classes of distributions: log-concave distribution, their convex combinations and product distributions. The standard i.i.d. assumption was significantly relaxed. These theorems and estimates can be used both for correction of high-dimensional data driven AI systems and for analysis of their vulnerabilities. The third area of application is the emergence of memories in ensembles of neurons, the phenomena of grandmother's cells and sparse coding in the brain, and explanation of unexpected effectiveness of small neural ensembles in high-dimensional brain.

Augmented Artificial Intelligence: a Conceptual Framework

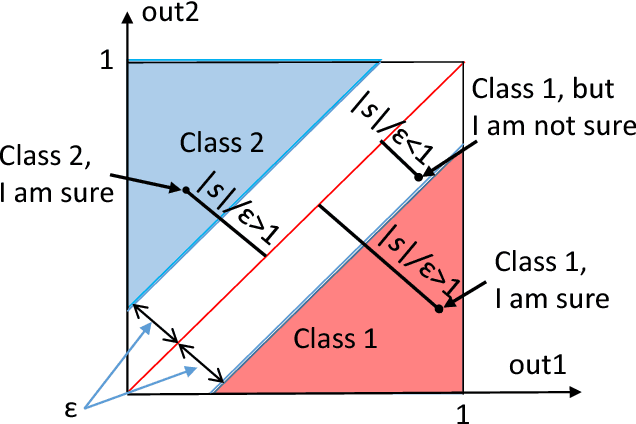
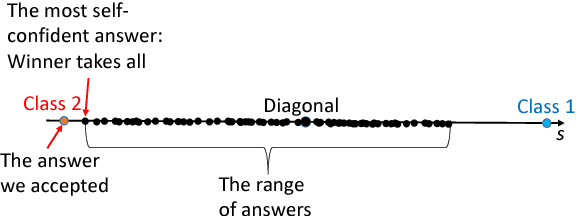
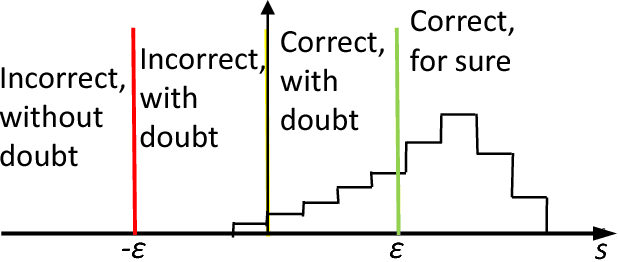
All artificial Intelligence (AI) systems make errors. These errors are unexpected, and differ often from the typical human mistakes ("non-human" errors). The AI errors should be corrected without damage of existing skills and, hopefully, avoiding direct human expertise. This paper presents an initial summary report of project taking new and systematic approach to improving the intellectual effectiveness of the individual AI by communities of AIs. We combine some ideas of learning in heterogeneous multiagent systems with new and original mathematical approaches for non-iterative corrections of errors of legacy AI systems. The mathematical foundations of AI non-destructive correction are presented and a series of new stochastic separation theorems is proven. These theorems provide a new instrument for the development, analysis, and assessment of machine learning methods and algorithms in high dimension. They demonstrate that in high dimensions and even for exponentially large samples, linear classifiers in their classical Fisher's form are powerful enough to separate errors from correct responses with high probability and to provide efficient solution to the non-destructive corrector problem. In particular, we prove some hypotheses formulated in our paper `Stochastic Separation Theorems' (Neural Networks, 94, 255--259, 2017), and answer one general problem published by Donoho and Tanner in 2009.