Logistic-beta processes for modeling dependent random probabilities with beta marginals

The beta distribution serves as a canonical tool for modeling probabilities and is extensively used in statistics and machine learning, especially in the field of Bayesian nonparametrics. Despite its widespread use, there is limited work on flexible and computationally convenient stochastic process extensions for modeling dependent random probabilities. We propose a novel stochastic process called the logistic-beta process, whose logistic transformation yields a stochastic process with common beta marginals. Similar to the Gaussian process, the logistic-beta process can model dependence on both discrete and continuous domains, such as space or time, and has a highly flexible dependence structure through correlation kernels. Moreover, its normal variance-mean mixture representation leads to highly effective posterior inference algorithms. The flexibility and computational benefits of logistic-beta processes are demonstrated through nonparametric binary regression simulation studies. Furthermore, we apply the logistic-beta process in modeling dependent Dirichlet processes, and illustrate its application and benefits through Bayesian density regression problems in a toxicology study.

Variational sparse inverse Cholesky approximation for latent Gaussian processes via double Kullback-Leibler minimization

To achieve scalable and accurate inference for latent Gaussian processes, we propose a variational approximation based on a family of Gaussian distributions whose covariance matrices have sparse inverse Cholesky (SIC) factors. We combine this variational approximation of the posterior with a similar and efficient SIC-restricted Kullback-Leibler-optimal approximation of the prior. We then focus on a particular SIC ordering and nearest-neighbor-based sparsity pattern resulting in highly accurate prior and posterior approximations. For this setting, our variational approximation can be computed via stochastic gradient descent in polylogarithmic time per iteration. We provide numerical comparisons showing that the proposed double-Kullback-Leibler-optimal Gaussian-process approximation (DKLGP) can sometimes be vastly more accurate than alternative approaches such as inducing-point and mean-field approximations at similar computational complexity.

Why the Rich Get Richer? On the Balancedness of Random Partition Models

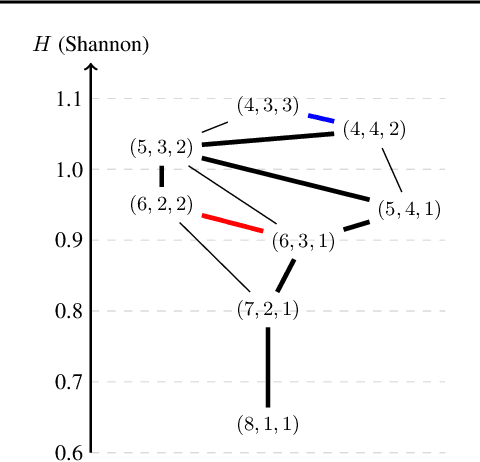
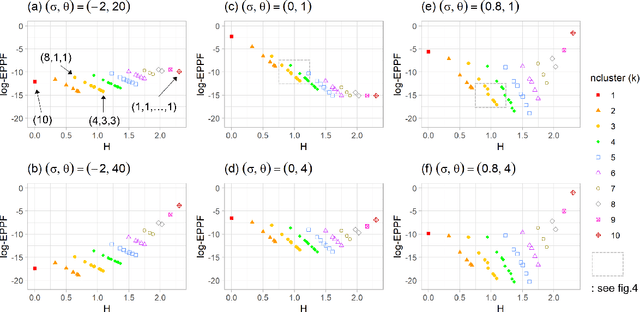
Random partition models are widely used in Bayesian methods for various clustering tasks, such as mixture models, topic models, and community detection problems. While the number of clusters induced by random partition models has been studied extensively, another important model property regarding the balancedness of cluster sizes has been largely neglected. We formulate a framework to define and theoretically study the balancedness of exchangeable random partition models, by analyzing how a model assigns probabilities to partitions with different levels of balancedness. We demonstrate that the "rich-get-richer" characteristic of many existing popular random partition models is an inevitable consequence of two common assumptions: product-form exchangeability and projectivity. We propose a principled way to compare the balancedness of random partition models, which gives a better understanding of what model works better and what doesn't for different applications. We also introduce the "rich-get-poorer" random partition models and illustrate their application to entity resolution tasks.

Row-clustering of a Point Process-valued Matrix

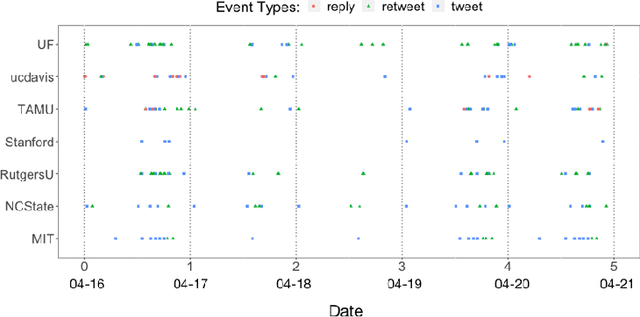
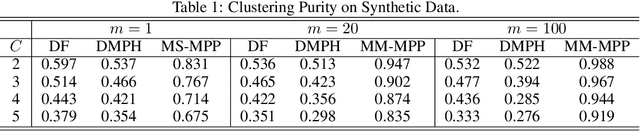
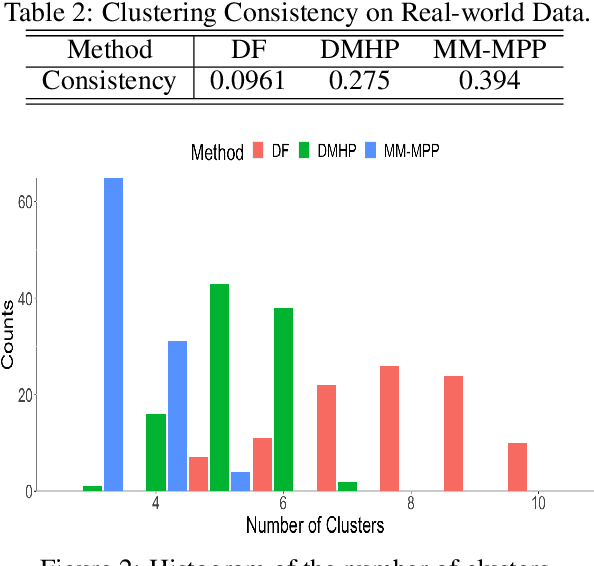
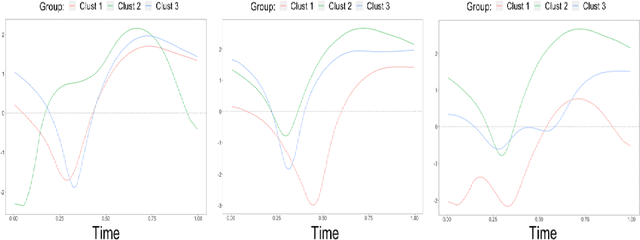
Structured point process data harvested from various platforms poses new challenges to the machine learning community. By imposing a matrix structure to repeatedly observed marked point processes, we propose a novel mixture model of multi-level marked point processes for identifying potential heterogeneity in the observed data. Specifically, we study a matrix whose entries are marked log-Gaussian Cox processes and cluster rows of such a matrix. An efficient semi-parametric Expectation-Solution (ES) algorithm combined with functional principal component analysis (FPCA) of point processes is proposed for model estimation. The effectiveness of the proposed framework is demonstrated through simulation studies and a real data analysis.

T-LoHo: A Bayesian Regularization Model for Structured Sparsity and Smoothness on Graphs

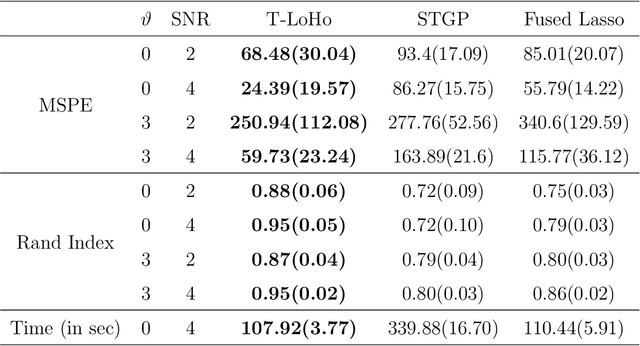
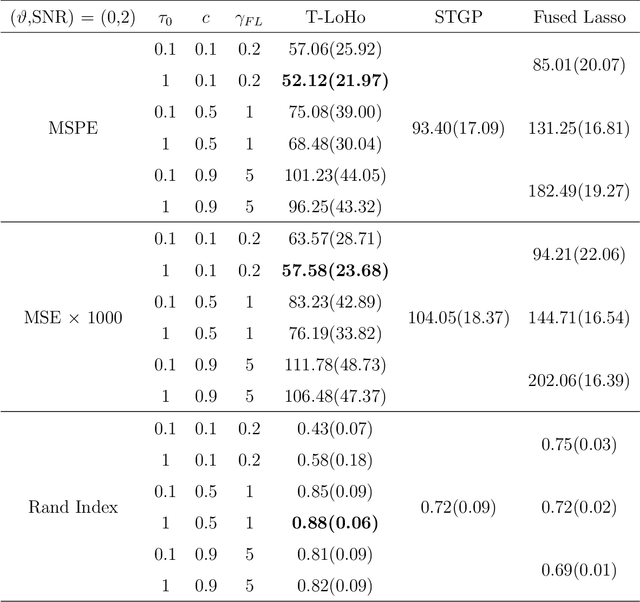
Many modern complex data can be represented as a graph. In models dealing with graph-structured data, multivariate parameters are not just sparse but have structured sparsity and smoothness in the sense that both zero and non-zero parameters tend to cluster together. We propose a new prior for high dimensional parameters with graphical relations, referred to as a Tree-based Low-rank Horseshoe(T-LoHo) model, that generalizes the popular univariate Bayesian horseshoe shrinkage prior to the multivariate setting to detect structured sparsity and smoothness simultaneously. The prior can be embedded in many hierarchical high dimensional models. To illustrate its utility, we apply it to regularize a Bayesian high-dimensional regression problem where the regression coefficients are linked on a graph. The resulting clusters have flexible shapes and satisfy the cluster contiguity constraint with respect to the graph. We design an efficient Markov chain Monte Carlo algorithm that delivers full Bayesian inference with uncertainty measures for model parameters including the number of clusters. We offer theoretical investigations of the clustering effects and posterior concentration results. Finally, we illustrate the performance of the model with simulation studies and real data applications such as anomaly detection in road networks. The results indicate substantial improvements over other competing methods such as sparse fused lasso.

Cognitive Learning of Statistical Primary Patterns via Bayesian Network

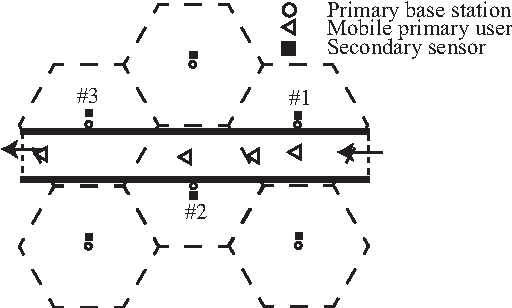
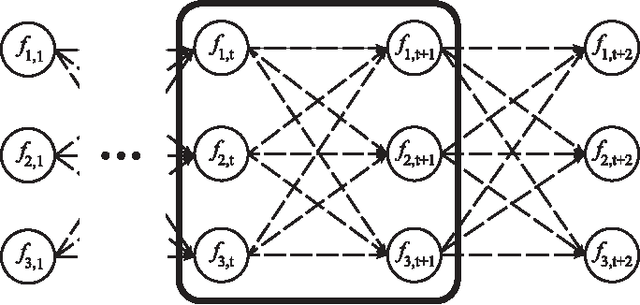
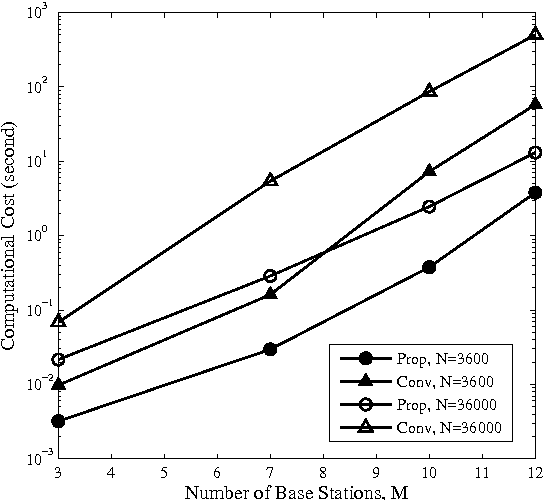
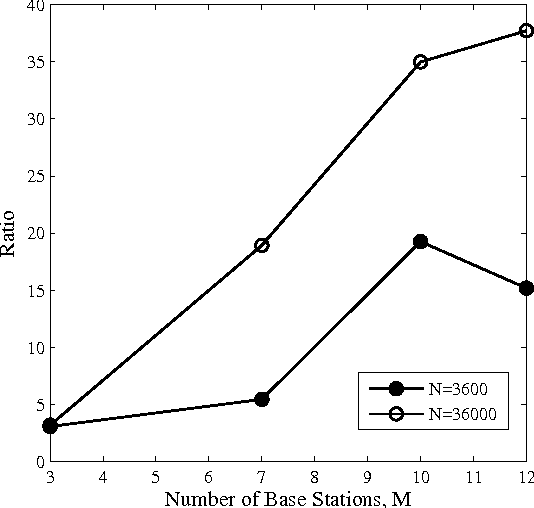
In cognitive radio (CR) technology, the trend of sensing is no longer to only detect the presence of active primary users. A large number of applications demand for more comprehensive knowledge on primary user behaviors in spatial, temporal, and frequency domains. To satisfy such requirements, we study the statistical relationship among primary users by introducing a Bayesian network (BN) based framework. How to learn such a BN structure is a long standing issue, not fully understood even in the statistical learning community. Besides, another key problem in this learning scenario is that the CR has to identify how many variables are in the BN, which is usually considered as prior knowledge in statistical learning applications. To solve such two issues simultaneously, this paper proposes a BN structure learning scheme consisting of an efficient structure learning algorithm and a blind variable identification scheme. The proposed approach incurs significantly lower computational complexity compared with previous ones, and is capable of determining the structure without assuming much prior knowledge about variables. With this result, cognitive users could efficiently understand the statistical pattern of primary networks, such that more efficient cognitive protocols could be designed across different network layers.