Importance Weighted Score Matching for Diffusion Samplers with Enhanced Mode Coverage

Training neural samplers directly from unnormalized densities without access to target distribution samples presents a significant challenge. A critical desideratum in these settings is achieving comprehensive mode coverage, ensuring the sampler captures the full diversity of the target distribution. However, prevailing methods often circumvent the lack of target data by optimizing reverse KL-based objectives. Such objectives inherently exhibit mode-seeking behavior, potentially leading to incomplete representation of the underlying distribution. While alternative approaches strive for better mode coverage, they typically rely on implicit mechanisms like heuristics or iterative refinement. In this work, we propose a principled approach for training diffusion-based samplers by directly targeting an objective analogous to the forward KL divergence, which is conceptually known to encourage mode coverage. We introduce \textit{Importance Weighted Score Matching}, a method that optimizes this desired mode-covering objective by re-weighting the score matching loss using tractable importance sampling estimates, thereby overcoming the absence of target distribution data. We also provide theoretical analysis of the bias and variance for our proposed Monte Carlo estimator and the practical loss function used in our method. Experiments on increasingly complex multi-modal distributions, including 2D Gaussian Mixture Models with up to 120 modes and challenging particle systems with inherent symmetries -- demonstrate that our approach consistently outperforms existing neural samplers across all distributional distance metrics, achieving state-of-the-art results on all benchmarks.

Row-clustering of a Point Process-valued Matrix

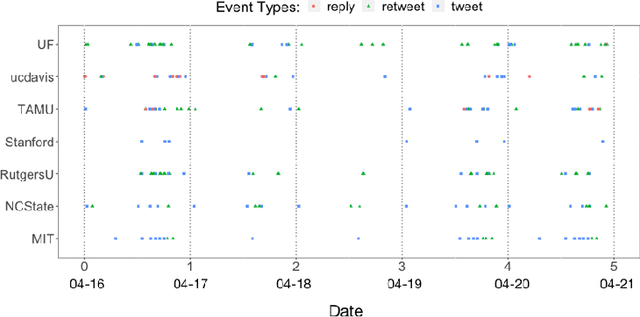
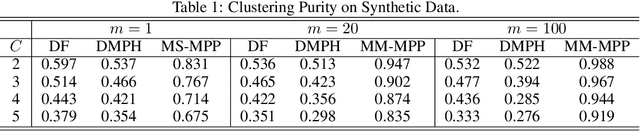
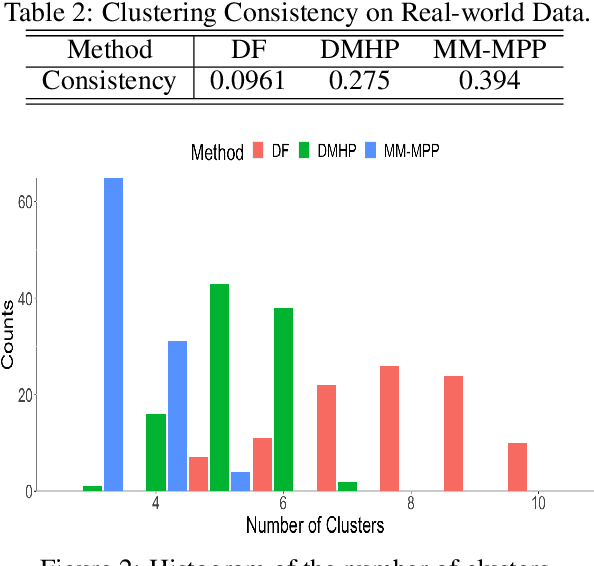
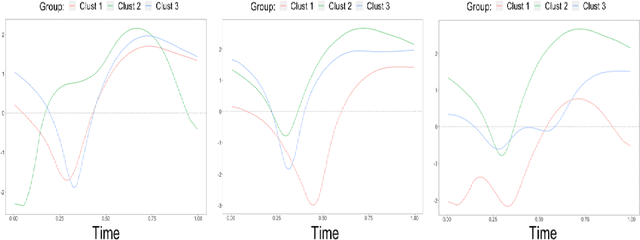
Structured point process data harvested from various platforms poses new challenges to the machine learning community. By imposing a matrix structure to repeatedly observed marked point processes, we propose a novel mixture model of multi-level marked point processes for identifying potential heterogeneity in the observed data. Specifically, we study a matrix whose entries are marked log-Gaussian Cox processes and cluster rows of such a matrix. An efficient semi-parametric Expectation-Solution (ES) algorithm combined with functional principal component analysis (FPCA) of point processes is proposed for model estimation. The effectiveness of the proposed framework is demonstrated through simulation studies and a real data analysis.

Latent Network Structure Learning from High Dimensional Multivariate Point Processes

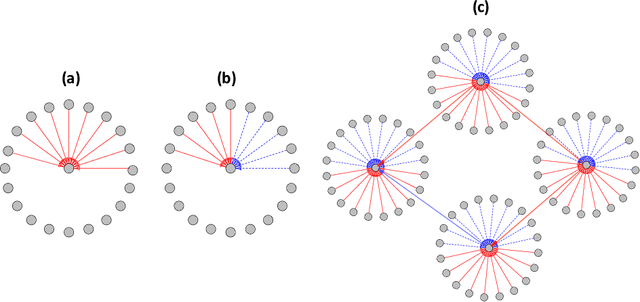
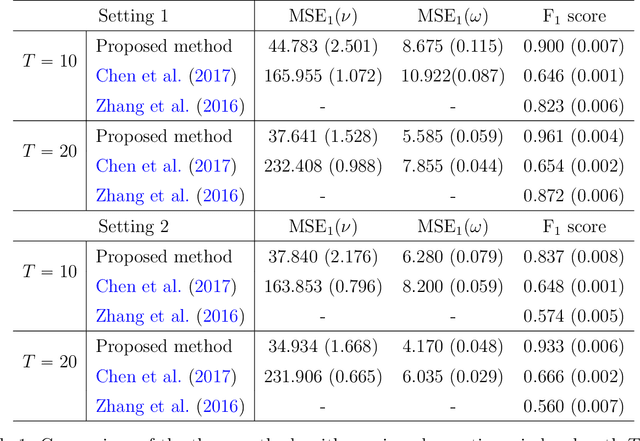
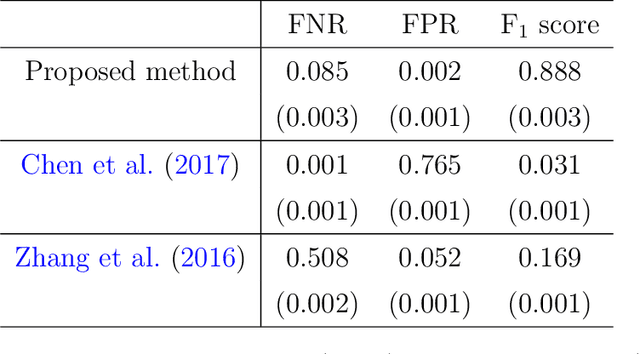
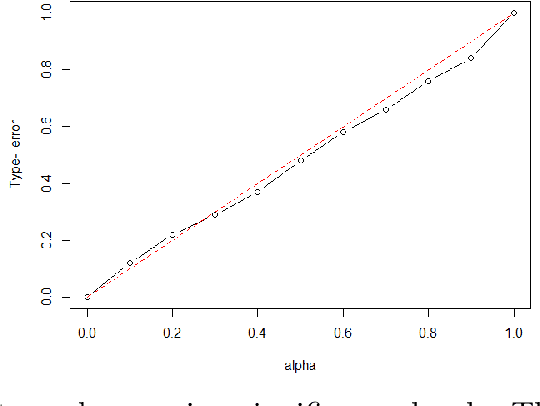
Learning the latent network structure from large scale multivariate point process data is an important task in a wide range of scientific and business applications. For instance, we might wish to estimate the neuronal functional connectivity network based on spiking times recorded from a collection of neurons. To characterize the complex processes underlying the observed data, we propose a new and flexible class of nonstationary Hawkes processes that allow both excitatory and inhibitory effects. We estimate the latent network structure using an efficient sparse least squares estimation approach. Using a thinning representation, we establish concentration inequalities for the first and second order statistics of the proposed Hawkes process. Such theoretical results enable us to establish the non-asymptotic error bound and the selection consistency of the estimated parameters. Furthermore, we describe a penalized least squares based statistic for testing if the background intensity is constant in time. We demonstrate the efficacy of our proposed method through simulation studies and an application to a neuron spike train data set.