Probabilistic Skip Connections for Deterministic Uncertainty Quantification in Deep Neural Networks

Deterministic uncertainty quantification (UQ) in deep learning aims to estimate uncertainty with a single pass through a network by leveraging outputs from the network's feature extractor. Existing methods require that the feature extractor be both sensitive and smooth, ensuring meaningful input changes produce meaningful changes in feature vectors. Smoothness enables generalization, while sensitivity prevents feature collapse, where distinct inputs are mapped to identical feature vectors. To meet these requirements, current deterministic methods often retrain networks with spectral normalization. Instead of modifying training, we propose using measures of neural collapse to identify an existing intermediate layer that is both sensitive and smooth. We then fit a probabilistic model to the feature vector of this intermediate layer, which we call a probabilistic skip connection (PSC). Through empirical analysis, we explore the impact of spectral normalization on neural collapse and demonstrate that PSCs can effectively disentangle aleatoric and epistemic uncertainty. Additionally, we show that PSCs achieve uncertainty quantification and out-of-distribution (OOD) detection performance that matches or exceeds existing single-pass methods requiring training modifications. By retrofitting existing models, PSCs enable high-quality UQ and OOD capabilities without retraining.

Learning non-Gaussian spatial distributions via Bayesian transport maps with parametric shrinkage

Many applications, including climate-model analysis and stochastic weather generators, require learning or emulating the distribution of a high-dimensional and non-Gaussian spatial field based on relatively few training samples. To address this challenge, a recently proposed Bayesian transport map (BTM) approach consists of a triangular transport map with nonparametric Gaussian-process (GP) components, which is trained to transform the distribution of interest distribution to a Gaussian reference distribution. To improve the performance of this existing BTM, we propose to shrink the map components toward a ``base'' parametric Gaussian family combined with a Vecchia approximation for scalability. The resulting ShrinkTM approach is more accurate than the existing BTM, especially for small numbers of training samples. It can even outperform the ``base'' family when trained on a single sample of the spatial field. We demonstrate the advantage of ShrinkTM though numerical experiments on simulated data and on climate-model output.

Vecchia Gaussian Process Ensembles on Internal Representations of Deep Neural Networks

For regression tasks, standard Gaussian processes (GPs) provide natural uncertainty quantification, while deep neural networks (DNNs) excel at representation learning. We propose to synergistically combine these two approaches in a hybrid method consisting of an ensemble of GPs built on the output of hidden layers of a DNN. GP scalability is achieved via Vecchia approximations that exploit nearest-neighbor conditional independence. The resulting deep Vecchia ensemble not only imbues the DNN with uncertainty quantification but can also provide more accurate and robust predictions. We demonstrate the utility of our model on several datasets and carry out experiments to understand the inner workings of the proposed method.

Variational sparse inverse Cholesky approximation for latent Gaussian processes via double Kullback-Leibler minimization

To achieve scalable and accurate inference for latent Gaussian processes, we propose a variational approximation based on a family of Gaussian distributions whose covariance matrices have sparse inverse Cholesky (SIC) factors. We combine this variational approximation of the posterior with a similar and efficient SIC-restricted Kullback-Leibler-optimal approximation of the prior. We then focus on a particular SIC ordering and nearest-neighbor-based sparsity pattern resulting in highly accurate prior and posterior approximations. For this setting, our variational approximation can be computed via stochastic gradient descent in polylogarithmic time per iteration. We provide numerical comparisons showing that the proposed double-Kullback-Leibler-optimal Gaussian-process approximation (DKLGP) can sometimes be vastly more accurate than alternative approaches such as inducing-point and mean-field approximations at similar computational complexity.

Scalable Bayesian Optimization Using Vecchia Approximations of Gaussian Processes

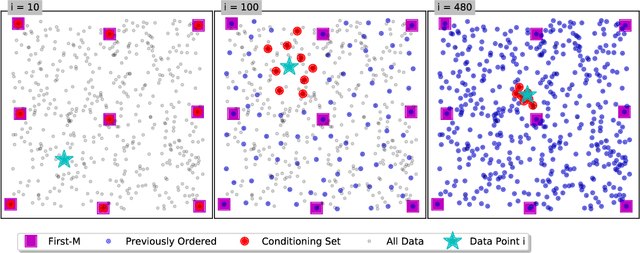
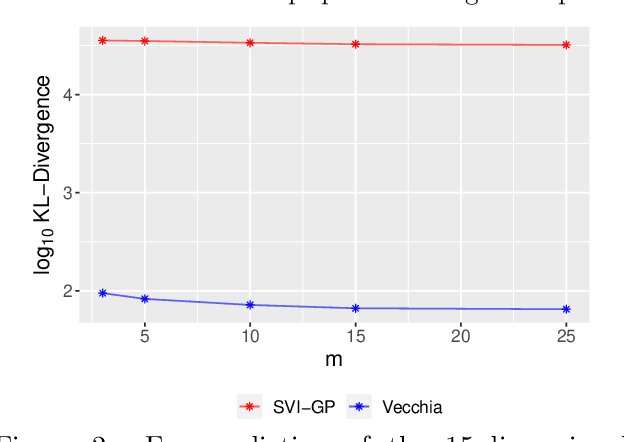
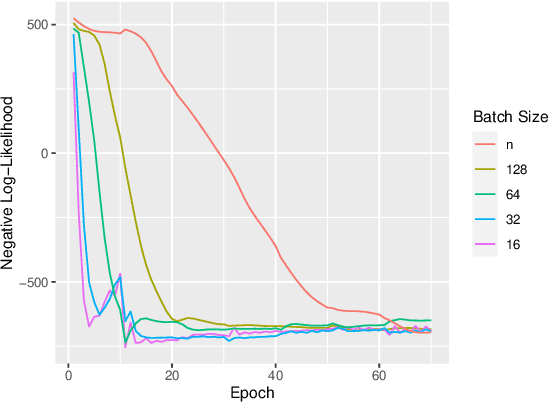
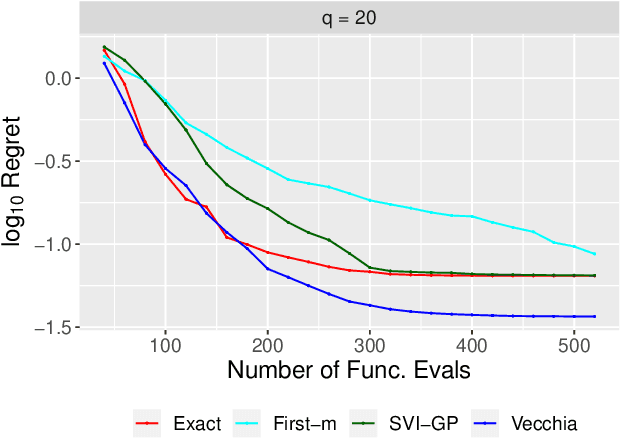
Bayesian optimization is a technique for optimizing black-box target functions. At the core of Bayesian optimization is a surrogate model that predicts the output of the target function at previously unseen inputs to facilitate the selection of promising input values. Gaussian processes (GPs) are commonly used as surrogate models but are known to scale poorly with the number of observations. We adapt the Vecchia approximation, a popular GP approximation from spatial statistics, to enable scalable high-dimensional Bayesian optimization. We develop several improvements and extensions, including training warped GPs using mini-batch gradient descent, approximate neighbor search, and selecting multiple input values in parallel. We focus on the use of our warped Vecchia GP in trust-region Bayesian optimization via Thompson sampling. On several test functions and on two reinforcement-learning problems, our methods compared favorably to the state of the art.

Scalable Gaussian-process regression and variable selection using Vecchia approximations

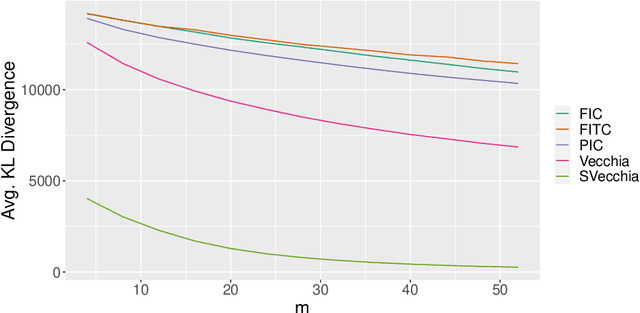
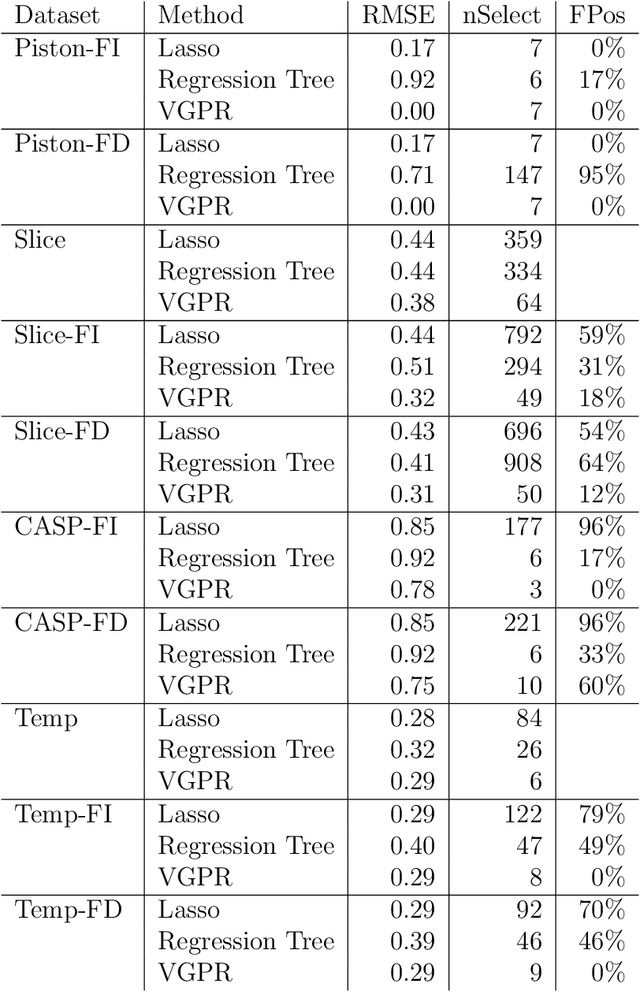
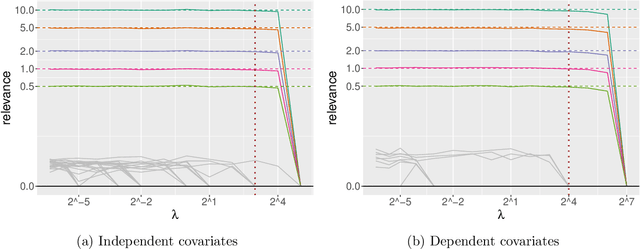
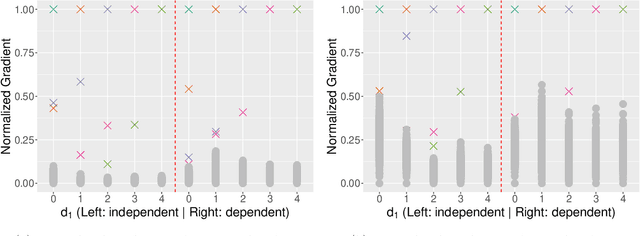
Gaussian process (GP) regression is a flexible, nonparametric approach to regression that naturally quantifies uncertainty. In many applications, the number of responses and covariates are both large, and a goal is to select covariates that are related to the response. For this setting, we propose a novel, scalable algorithm, coined VGPR, which optimizes a penalized GP log-likelihood based on the Vecchia GP approximation, an ordered conditional approximation from spatial statistics that implies a sparse Cholesky factor of the precision matrix. We traverse the regularization path from strong to weak penalization, sequentially adding candidate covariates based on the gradient of the log-likelihood and deselecting irrelevant covariates via a new quadratic constrained coordinate descent algorithm. We propose Vecchia-based mini-batch subsampling, which provides unbiased gradient estimators. The resulting procedure is scalable to millions of responses and thousands of covariates. Theoretical analysis and numerical studies demonstrate the improved scalability and accuracy relative to existing methods.

Scaled Vecchia approximation for fast computer-model emulation

Many scientific phenomena are studied using computer experiments consisting of multiple runs of a computer model while varying the input settings. Gaussian processes (GPs) are a popular tool for the analysis of computer experiments, enabling interpolation between input settings, but direct GP inference is computationally infeasible for large datasets. We adapt and extend a powerful class of GP methods from spatial statistics to enable the scalable analysis and emulation of large computer experiments. Specifically, we apply Vecchia's ordered conditional approximation in a transformed input space, with each input scaled according to how strongly it relates to the computer-model response. The scaling is learned from the data, by estimating parameters in the GP covariance function using Fisher scoring. Our methods are highly scalable, enabling estimation, joint prediction and simulation in near-linear time in the number of model runs. In several numerical examples, our approach substantially outperformed existing methods.